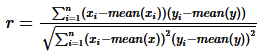Wykresy linii trendu i prostej regresji
Regresja liniowa
Średnie, mediany, odchylenia standardowe i ćwiartkowe charakteryzują pojedyncze zmienne liczbowe. W tym rozdziale omówiona zostanie regresja charakteryzująca dane mające postać par liczb. Chodzi i o pary uporządkowane. Pierwszą liczbą może być długość osobnika, druga jego ciężarem. Regresja między długością i ciężarem jest odpowiednikiem charakterystyki centralnej rozkładu, czyli np. wartości oczekiwanej albo mediany. Korelacja (a właściwie jej kwadrat) jest odpowiednikiem odchylenia standardowego. Jeżeli zatem w pracy zdecydujemy się podawać średnie i odchylenia standardowe bez nawiasów to regresje i korelacje powinny być potraktowane tak samo.
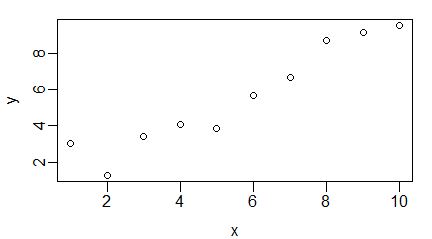
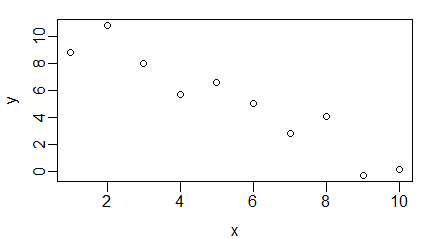
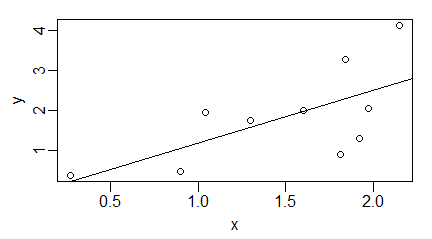
Regresja charakteryzuje zależność zmiennych liczbowych od siebie. Zależność ta mogłaby polegać na tym, że wzrost wartości jednej zmiennej zwiększa prawdopodobieństwo, że wartości drugiej zmiennej będą się zwiększać albo zmniejszać. Niekiedy taka zależność jest bardzo dobrze widoczna, jak na poniższych wykresach punktowych.
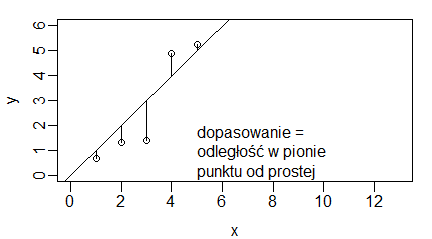
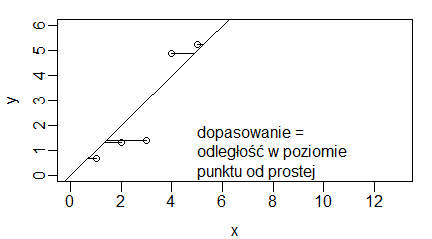
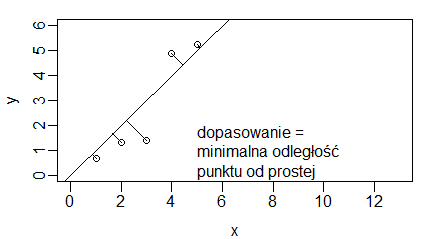
Zależność między zmiennymi najlepiej pokazałoby nachylenie prostej najlepiej dopasowanej do narysowanych danych. Kryteria takiego dopasowania mogłyby być bardzo różnie sformułowane. Po pierwsze należałoby określić w jaki sposób mierzymy dopasowanie pojedynczego punktu do prostej. Obrazują to następujące wykresy:
| x = 1:5 y = x + rnorm(5) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,x,x) text(5,1,”dopasowanie = \nodległość w pionie \npunktu od prostej”, adj=0) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,y,y) text(5,1,”dopasowanie = \nodległość w poziomie \npunktu od prostej”, adj=0) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,(x+y)/2,(x+y)/2) text(5,1,”dopasowanie = \nminimalna odległość \npunktu od prostej”, adj=0) |
Program ten tworzy trzy wykresy:
Po drugie, mając wiele pomiarów dopasowań pojedynczych punktów do prostej, należałoby zdecydować się na jakąś funkcję agregacyjną, by móc wyliczać dopasowanie prostej do danych, wskazywać lepiej lub gorzej dopasowane i ostatecznie wybrać prostą najlepszą. Takimi funkcjami aggregacyjnymi mogłyby być suma odległości, suma kwadratów odległości, średnia odległość i wiele innych funkcji.
Po ustaleniu reguł, dla każdej prostej y=ax+b i każdego zestawu par punktów (x1, x2 …, xn), (y1, y2, …, yn) można wyliczyć funkcję agregacyjną F((x1,x2,…,xn),(y1,y2,…,yn),ax+b). Należałoby znaleźć taką prostą (czyli takie a i b), dla której funkcja agregacyjna ma minimum. Sprowadza się do poszukiwania minimum lokalnego funkcji (a,b) → F((x1,x2,…,xn),(y1,y2,…,yn),ax+b). Wyznaczenie pochodnych cząstkowych tej funkcji dla a i b, przyrównanie ich do 0, pozwala na wyliczenie a i b, dla których funkcja agregująca ma minimum. To z kolei daje ogólny wzór na wyliczanie najlepiej dopasowanej prostej według przyjętych kryteriów do dowolnego zestawu danych.
Spośród najróżniejszych propozycji definiowania funkcji agregacyjnej najpopularniejsza jest definicja Karla Pearsona. Jest to suma kwadratów odległości. Natomiast odległości wylicza się w pionie i podnosi do kwadratu. Dla każdego punktu (x0,y0) wyznacza się jego odległość od prostej y=ax+b i wylicza (y0-ax0-b)2 a potem sumuje się uzyskane liczby. Wybiera się prostą dla której uzyskana suma jest najmniejsza. Metoda wyliczania takiej prostej nosi nazwę metody najmniejszych kwadratów, a prosta tak wyliczona nosi nazwę regresji (regresji z próby). Ma ona ogólną interpretację dla danych losowanych z rozkładu dwukrotnie normalnego. Założenia te dają następujące wzory na współczynniki prostej regresji:
Współczynniki prostej regresji łatwo jest zatem wyliczyć w R. Można dodać do wykresu rozrzutu wartości x można za pomocą funkcji abline(). Obowiązkowymi parametrami tej funkcji są dwie liczby, z których pierwsza to stała – punkt przecięcia wykreślanej prostej z osią 0Y, a druga to wsp. nachylenia czyli tangens kata nachylenia prostej do osi 0X. W skrypcie można zanotować następujący kod:
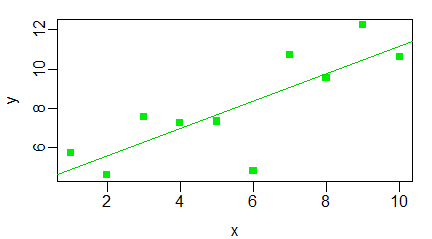
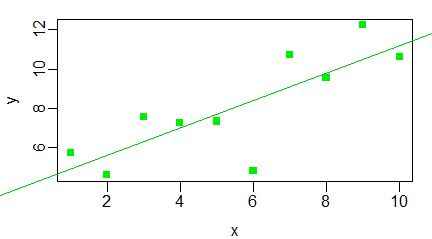
| x=1:10 y = c(5.76, 4.61, 7.59, 7.28, 7.34, 4.83, 10.71, 9.54, 12.23, 10.61) a=sum((x-mean(x))*(y-mean(y)))/sum((x-mean(x))^2) b=mean(y)-a*mean(x) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=FALSE) plot(x,y,col=”green2″, pch=15) abline(b,a,col=”green3″) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=TRUE) plot(x,y,col=”green2″, pch=15) abline(b,a,col=”green3″) |
Utworzony wykres na ogół spełnia wszystkie oczekiwania. Jeżeli jednak aktywna jest opcja xpd=TRUE funkcji par(), to linia trendu wyjdzie poza obszar kreślenia.
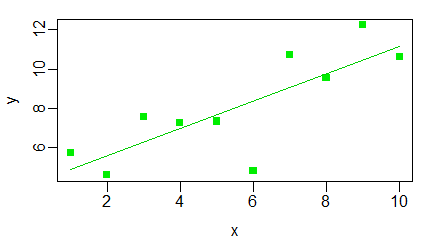
Tymczasem znacznie częściej linię trendu trzeba skrócić od minimalnej wartości x (w przykładzie 1) do maksymalnej wartości (w przykładzie 10). Wtedy lepiej skorzystać z funkcji podrzędnej lines(). Obowiązkowymi parametrami tej funkcji są współrzędne początku i końca linii zapisane jako c(min(x), max(x)) oraz c(min(y),max(y)). Można wykonać następujący program:
x=1:10 y = c(5.76, 4.61, 7.59, 7.28, 7.34, 4.83, 10.71, 9.54, 12.23, 10.61) a=sum((x-mean(x))*(y-mean(y)))/sum((x-mean(x))^2) b=mean(y)-a*mean(x) windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=TRUE) plot(x,y,col="green2", pch=15) lines(c(min(x),max(x)),c(a*min(x)+b,a*max(x)+b), col="green3") |
i uzyskać wykres:
W podanych programach parametry regresji wyliczane są ze wzorów. Tymczasem w R istnieje gotowa procedura na ich wyznaczenie. Służy do tego funkcja lm(), która zwraca tak naprawdę listę 12 różnych elementów, ale pierwszym elementem na liście są parametry (w kolejności b i a) prostej regresji y=ax+b. Tylko one się pokazują. Reszta wyników pojawia się gdy stosuje sie polecenia typu lm(y~x)[2] lub lm(y~x)[[5]]. Wygląda to następująco:
| > x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15) > y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12) > lm(y~x) # Call: lm(formula = y ~ x) # Coefficients: (Intercept) x -0.1084 1.3071 |
Przy tworzeniu wykresu rozrzutu danych z dodaną prostą regresji wystarczy zastosować funkcję abline() w postaci abline(lm(y~x)). Wykorzystano to w następującym programie:
x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15) y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12) windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0)) plot(x,y) abline(lm(y~x)) |
Wykonanie tego programu da w efekcie następujący wykres.
Trend
W biologii dość często pojawia się słowo trend (trend liniowy, trend rosnący, trend malejący, trend wykładniczy itp.). Słowa tego używano niegdyś jako szczególnej regresji, w której pierwsza zmienna (tzw. niezależna w myśl niezależności przyczynowo skutkowej) była wyrażana przez kolejne liczby (np. od 1 do 10 lub od 2001 do 2018). Odkąd jednak programy Microsoftu nazwały trendem każdą regresję (liniową i nieliniową) jest to synonim regresji. Do jego wyliczania używa się bowiem tak samo metody najmniejszych kwadratów.
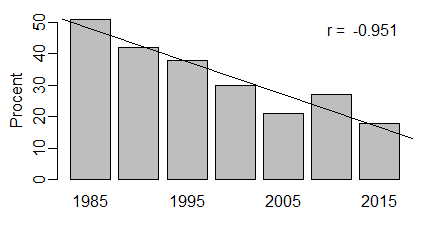
Czasem jednak jest wygodniej użyć słowa trend, niż regresja, gdy na przykład wykazuje jak w czasie zmniejszał się w populacji procent samców żółwi w miarę ocieplenia klimatu. Procenty obrazujemy za pomocą słupków, a regresję wylicza się dla ich wartości. Wygląda to następująco:
x=c(1985, 1990, 1995, 2000, 2005, 2010, 2015)
y=c(51, 42, 38, 30, 21, 27, 18)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
slup=barplot(y, names=x, ylab="Procent")
abline(lm(y~slup))
r=format(cor(slup,y),dig=3)
text(7.5,48,paste("r = ",r))
|
Wynikiem działania programu jest wykres słupkowy:
W programie nie użyto parametrów regresji między y a x, ale między y a środkami słupków, które są zapamiętywane w wektorze slup=barplot(). Funkcja barplot(), oprócz tego, że tworzy wykres, tworzy także wektor środków słupków, który można odczytać przez odpowiednie przypisanie. W tym typie wykresu układ współrzędnych dla słupków nie jest układem współrzędnych zależności y od x. Trzeba wyliczyć trend już po przeskalowaniu danych na rysunkowy układ współrzędnych.
Korelacja
Kwadrat korelacji, zwany współczynnikiem determinacji, odpowiednik odchylenia standardowego dla par punktów, definiuje się jako:
gdzie f(x) jest wartością regresji w punkcie x (czyli jest to ax+b). Ponieważ prosta, przyjmująca dla wszystkichch x stałą wartość równą średniej z wektora y, należy do rodziny funkcji, które dopasowujemy do danych metodą sumowania kwadratów odległości, licznik powyższego wzoru jest mniejszy niż mianownik. Im punkty są lepiej dopasowane do prostej regresji tym powyższy wzór daje większe liczby, a największą jest jeden.
Pierwiastek ze współczynnika determinacji R2, dodatni gdy nachylenie prostej regresji jest dodatnie i ujemny gdy nachylenie prostej regresji jest ujemne, nazywany jest współczynnikiem korelacji i oznaczany najczęściej jako r. Jego obliczanie w pracach biologicznych jest standardem. Po wprowadzeniu do niego wzorów na a i b dla regresji i kilku przekształceniach, można przekonać się, że:
Taki wzór znajdziecie we wszystkich podręcznikach statystyki.
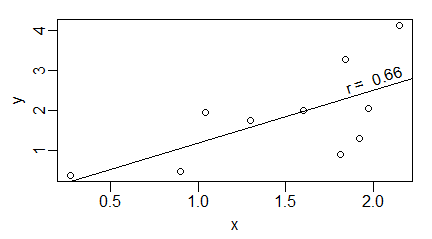
Oczywiście w R istnieje prosta funkcja wyliczająca współczynnik korelacji dla dwóch dowolnych wektorów liczbowych. Jest nią funkcja cor(). Standardem jest umieszczanie wartości współczynnika korelacji na wykresach regresji. Wygląda to następująco:
x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15)
y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
plot(x,y)
abline(lm(y~x))
r=format(cor(x,y),dig=3)
text(2,2.8,paste("r = ",r),srt=18)
|
Umiejscowienie napisu tak, by nie przesłaniało punktów oraz kąt obrotu, ustala się metodą prób i błędów.
Stężenie fluoru w wydzielinie gruczołów odbytowych skunksów i regresje liniowe dla wielu serii porównań
Baza danych, na której przykładzie pokazywane są różne programy w R, dotyczy samic i samców skunksów łowionych w trzech sezonach, które ważono i pobierano od nich próbki wydzieliny gruczołów odbytowych, a następnie określono stężenie fluoru w suchej masie tych próbek. Ta ramka danych została utworzona na podstawie danych pokazanych w części pierwszej “R Dla Biologów – Podstawowe Operacje” w rozdziale o ramkach danych w podrozdziale “Operacje na ramkach danych”.
Zobrazowanie zależności stężenia fluoru od ciężaru skunksów powinno być zrobione osobno grupach wyznaczonych przez ich płeć i sezon. Każda z 6 grup zwierząt powinna być zobrazowana przez inny kolor i powinna dla tej grupy zostać narysowana regresja w tym kolorze. Na początek można ustalić, że danym z wiosny dajemy kolor zielony (“green”), danym z jesieni kolor czerwony (“red”) a danym z zimy kolor niebieski (“blue”). Samice będą obrazowane przez pełne kółeczka (pch=19), a samce przez puste (pch=1). Tworzymy odpowiednie wektory pięćdziesięcioelementowe:
kolor=paste(1:50) for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="wiosna") kolor[i]="green" for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="jesień") kolor[i]="red" for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="zima") kolor[i]="blue" znak=1:50 for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samiec") znak[i]=1 for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samica") znak[i]=19 |
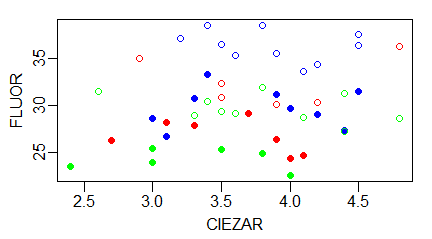
Pozwala to na narysowanie następującego wykresu:
windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0)) plot(FLUOR~CIEZAR, skunks, col=kolor, pch=znak) |
Powstaje w ten sposób wykres:
Następne instrukcje służyć będą do narysowania regresji dla każdej z grup punktów wyróżnionych przez PLEC i SEZON. Wykorzystana zostanie do tego funkcja by(), która podobnie jak aggregate() dzieli bazy danych na części wyróżnione przez wartości czynników, na których można potem wykonywać różne działania. W najprostszym przypadku instrukcja: by(skunks, list(skunks$PLEC, skunks$SEZON),
function(x) x) utworzy listę złożona z sześciu elementów, a każdy z tych elementów jest podbazą wyróżnioną przez wartości zmiennych dyskretnych. Parametry regresji, można wyliczyć za pomocą lm(y~x). Wykorzystując to można zastosować polecenie:
regresje = by(skunks, list(skunks$PLEC, skunks$SEZON), function(x) lm(FLUOR~CIEZAR,x)) |
Pojawi się lista, której obejrzenie pokazuje, że wyniki ukazały się kolejno dla: samice-jesień, samiec-jesień, samice-wiosna, samiec-wiosna, samice-zima, samiec-zima. Ponieważ chcemy by kolory regresji zgadzały się z kolorem punktów i dla samic wyrażone były linią ciągłą, a dla samców przerywaną, to powinniśmy utworzyć następujące wektory kolorów i typów linii:
kolor.regresji = rep(c("red","green","blue"), each=2)
typ.regresji = rep(1:2,3)
|
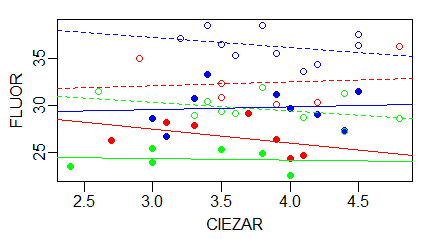
Do wykonanego wykresu można teraz dodać linie trendu
for (i in 1:6) abline(regresje[[i]], col=kolor.regresji[i], lty=typ.regresji[i]) |
Powstaje w ten sposób następujący wykres;
Wykres ten ma wiele niedociągnięć. Po pierwsze nie ma legendy i w dodatku nie ma miejsca na legendę. Po drugie podpisy osi (domyślnie wstawiane nazwy kolumn bazy danych), są niepoprawne. Trzeba je wprowadzić. Aby utworzyć legendę i zmienić podpisy należy zebrać wszystkie instrukcje do skryptu i wykonać stosowne poprawki.
kolor=paste(1:50)
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="wiosna") kolor[i]="green"
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="jesień") kolor[i]="red"
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="zima") kolor[i]="blue"
znak=1:50
for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samiec") znak[i]=1
for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samica") znak[i]=19
windows(5.5, 2.5)
# wydłużenie wykresu w poziomie o 1 cal)
par(mar=c(3,3,1,10), mgp=c(1.7,0.5,0))
# wydłużenie prawego marginesu o 9 linijek)
# dołączenie do funkcji plot() podpisów osi
plot(FLUOR~CIEZAR, skunks, col=kolor, pch=znak,
xlab="Ciężar [kg]",
ylab=expression("Stężenie fluoru [ " * ng %.% g^-1 *"]" ) )
regresje = by(skunks, list(skunks$PLEC, skunks$SEZON),
function(x) lm(FLUOR~CIEZAR,x))
kolor.regresji = rep(c("red","green","blue"), each=2)
typ.regresji = rep(1:2,3)
for (i in 1:6) abline(regresje[[i]], col=kolor.regresji[i],
lty=typ.regresji[i])
#
# dorysowanie legendy
par(xpd=TRUE)
legend(5,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("samice wiosną", "samice-jesienią", "samice zimą",
"samce wiosną", "samce jesienią", "samce zimą"),
lty=c(1,1,1,2,2,2), pch=c(19,19,19,1,1,1),
col=c("green", "red", "blue"), bty="n")
|
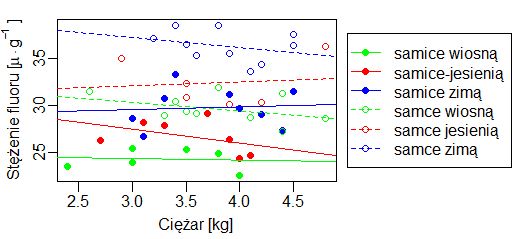
Powstał w ten sposób wykres:
Wykres ten można dalej modyfikować. Można zmienić wielkość i krój czcionki, co opisano w rozdziale 8. Można użyć innych kolorów (rozdział 6), znaczników punktów (rozdział 7), zastosować kolorowe tło (rozdział 6). Można także zdecydować się na wyliczanie korelacji dla każdej regresji i dopisanie jej w odpowiednim miejscu i w odpowiednim kolorze na wykresie. Ma to znaczenie w przypadku gdy regresje są silnie nachylone, bo w przypadku pokazanych skunksów jest to zbędna informacja. Wystarczy tylko podpatrzeć, jak to zostało zaprogramowane, by wprowadzić stosowne poprawki do własnego kodu.