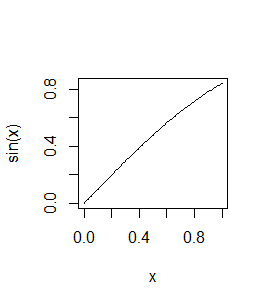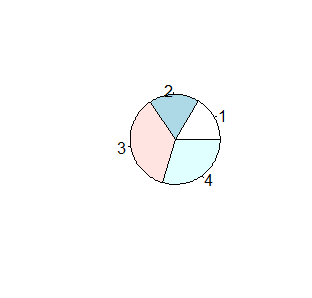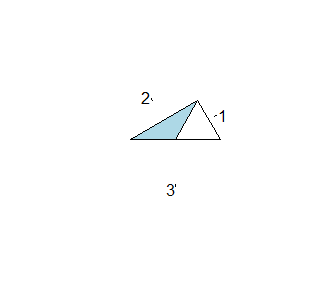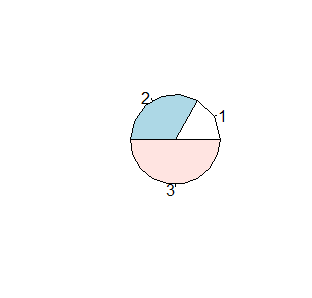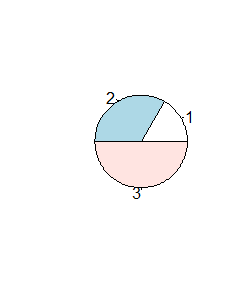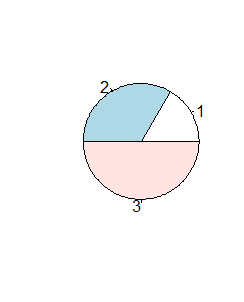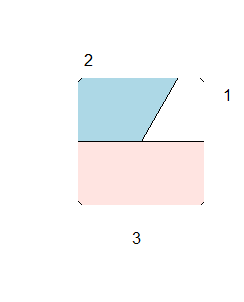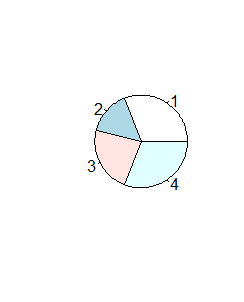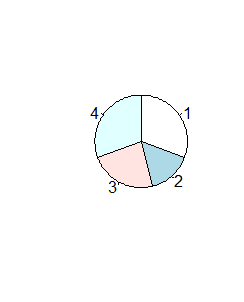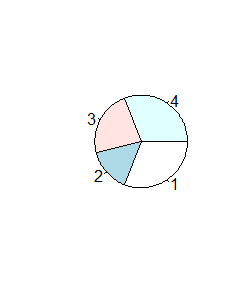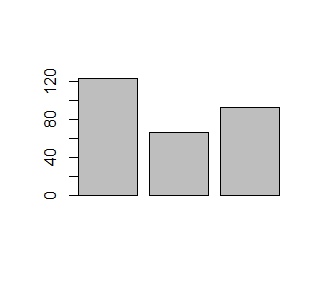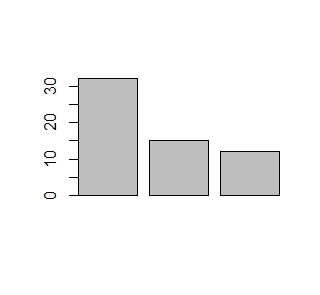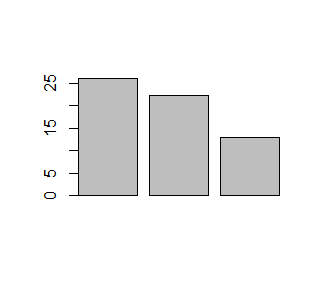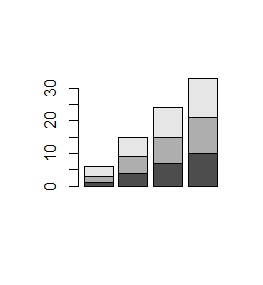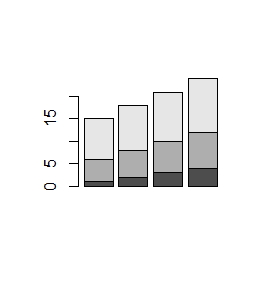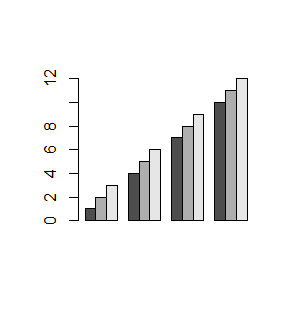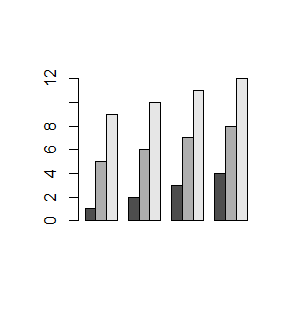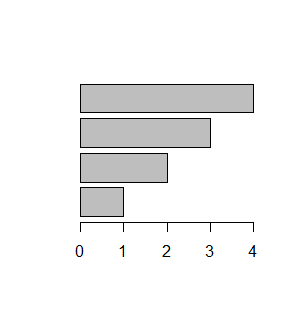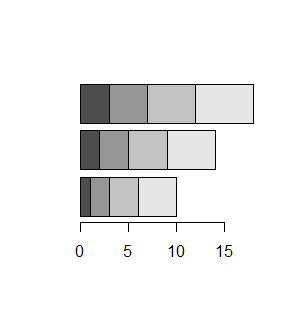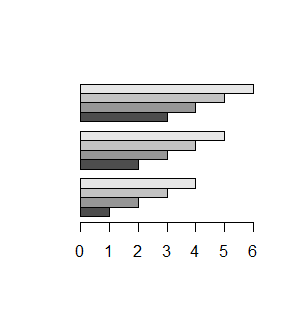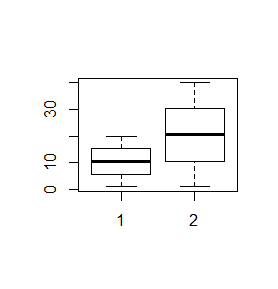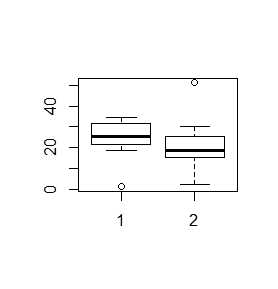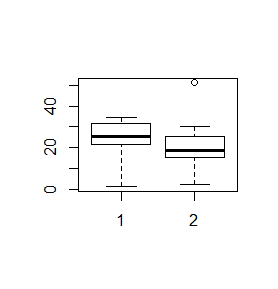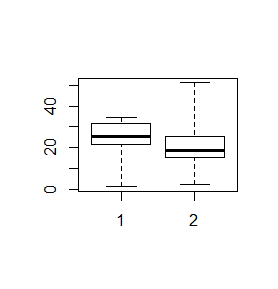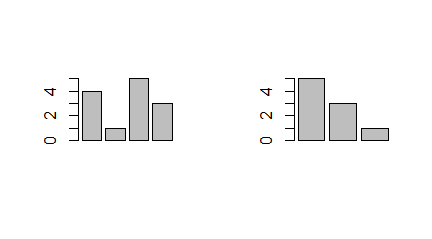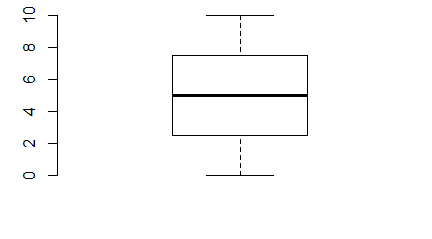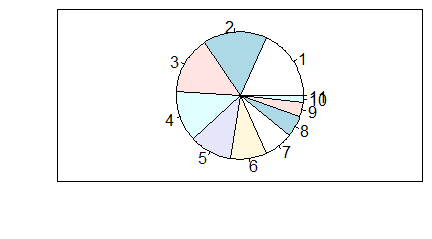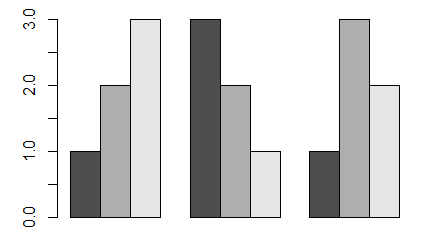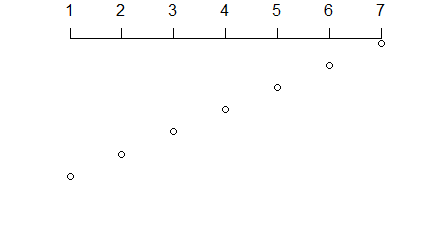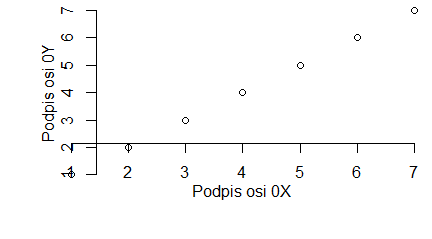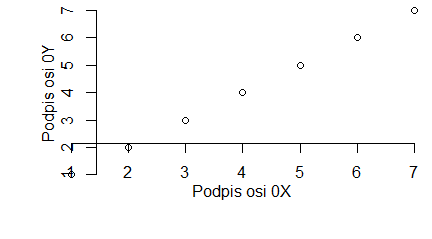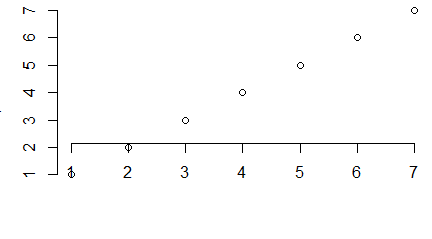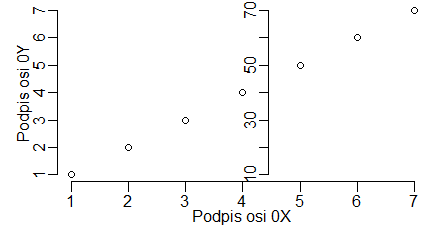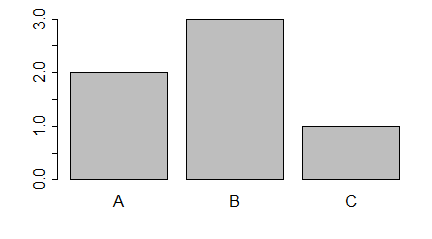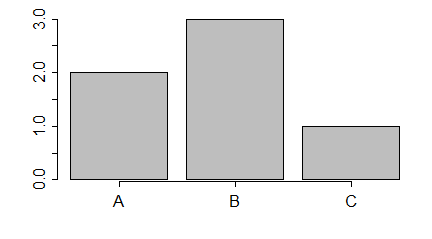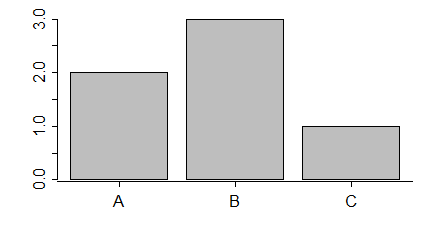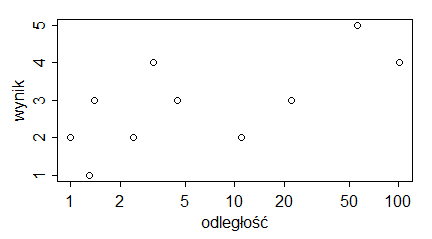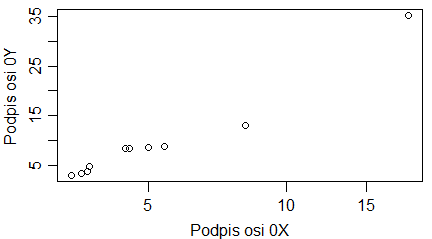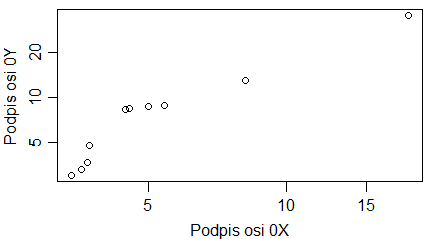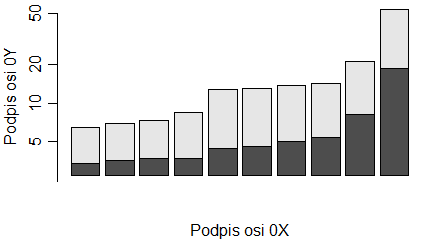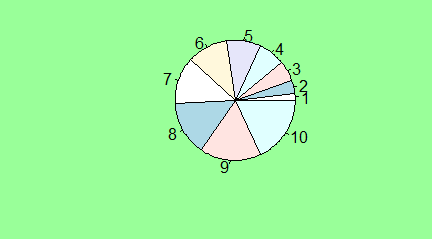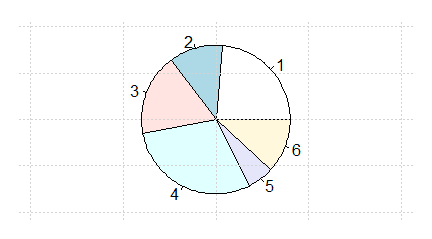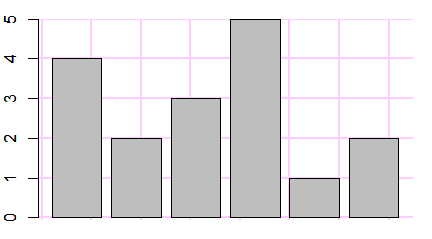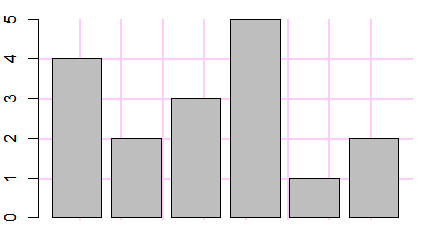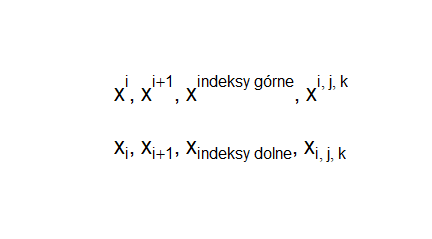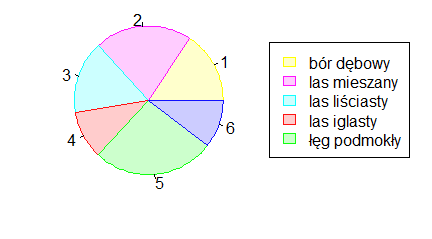R, operacje graficzne
Miłosława Sokół
R dla Biologów, operacje graficzne
Zasady cytowania podręcznika: Miłosława Sokół (2023) “R dla Biologów, operacje graficzne”, Wydział Biologii Uniwersytetu Warszawskiego, online: https://skrypty.biol.uw.edu.pl/r-grafika
Uwagi o grafice R
Opis funkcji graficznych, którymi posługuje się R to pod wieloma względami najprzydatniejsza część mojego podręcznika. Dotyczy bowiem obrazowania wyników badań i możliwość wykonania wykresu wysokiej jakości, który akceptują najbardziej wymagające wydawnictwa naukowe.
Człowiek jest wzrokowcem i odpowiednie hipotezy stawia, gdy zobaczy różnice na wykresie. Znacznie trudniej ocenia liczby w tabelach. Obecnie wykształcił się pewien standard opracowania danych biologicznych, w którym wykresy pełnią podstawową rolę. Proponujemy ich wykonanie w R. Do tego programu zostały włączone procedury środowiska graficznego GNOME będące częścią projektu GNU. Projekt GNOME rozpoczęto w sierpniu 1997 roku przez Miguela de Icaza w celu stworzenia w pełni wolnodostępnego graficznego środowiska użytkownika dla systemu GNU/Linux. Rozwijany był później przez rzeszę programistów-ochotników współpracujących ze sobą poprzez listy dyskusyjne. Część tych procedur została zaadoptowana do R, przy pewnym ujednoliceniu składni. W rezultacie w R można zrobić więcej wykresów, niż w wielu innych popularnych programach (np. Excelu), zapamiętać je jako obiekty rastrowe w kilku standardach i dowolnie ustalonej rozdzielczości albo jako obiekty wektorowe. Tych ostatnich domagają się często wydawnictwa, gdy chcą opublikować daną pracę.
Procedury graficzne zgromadzono w pakiecie graphics, która jest ładowana standardowo do R. Nie trzeba jej wywoływać poleceniem require() lub library(). Dodatkowo istnieje kilka popularnych pakietów graficznych, które wzbogacają możliwości graficzne R. Należą do nich Lattice, ggplot2, iplots, scatterplot3d, diagram i inne. Można je załadować do R poleceniem pobierz pakiet i następnie używać po uruchomieniu funkcji require(nazwa_pakietu) albo library(nazwa_pakietu).
Stosowanie grafiki w R polega na zastosowaniu funkcji graficznej, która uruchamia okienko graficzne i powoduje powstanie wykresu. Funkcje te tworzą okno graficzne o domyślnych wymiarach, wielkościach marginesów i innych opcjach, i rysują w nim wykres. Procedurę tę mogą poprzedzać polecenia modyfikujące standardową wielkość okna graficznego, jego organizacje (np. wielkość marginesu, liczbę i miejsce kolejnych wykresów, gdy chce się umieścić ich w oknie graficznym kilka), opcje związane z wielkością i krojem czcionki i wiele innych. Kolejnym krokiem jest wykonanie funkcji graficznej tworzącej jakiś wykres. Ponadto procedury graficzne na ogół posiadają wiele opcji, które pozwalają na modyfikacje wykresu. Po wykonaniu funkcji graficznej i pojawieniu się wykresu w osobnym oknie, można na niego nałożyć dodatkowe elementy, napisy, podpisy za pomocą kolejnych poleceń. Innymi słowy funkcje graficzne w R dzielą się na nadrzędne (draw graphics functions), zwane czasem rysującymi i podrzędne funkcje graficzne (add graphics functions) zwane dokładającymi. Struktura programu tworzącego wykres wygląda następująco: Trzy gwiazdki oznaczają instrukcję konieczną do powstania wykresu. Pozostałe instrukcje mają wartości domyślne i nie są obowiązkowe. Jednak wykresy z opcjami domyślnymi z reguły wymagają korekty.
Trzy gwiazdki oznaczają instrukcję konieczną do powstania wykresu. Pozostałe instrukcje mają wartości domyślne i nie są obowiązkowe. Jednak wykresy z opcjami domyślnymi z reguły wymagają korekty.
Struktura ta powoduje, że zrobienie wykresu wymaga napisania programu złożonego z wielu linijek. Robi się to na ogół w skryptach, które zapamiętuje się razem z bazą danych związanych z konkretnymi badaniami. Ponieważ na ogół w pracach biologicznych wykonuje się wiele wykresów, kolejne z nich tworzy się kopiując ustaloną przy pierwszym wykresie strukturę (np. wielkość i krój czcionki, umiejscowienie tekstów na wykresie itp.). Przyśpiesza to pracę i umożliwia tworzenie w pełni do siebie pasującego opracowania graficznego danych.
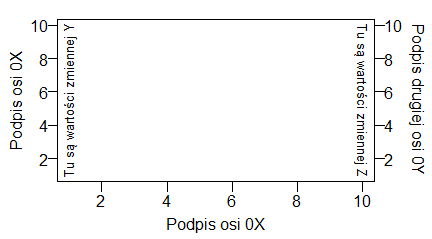
Część tę przeznaczono dla użytkowników, którzy opracowując własne dane, tworzą wykresy, a następnie je modyfikują. Zastosowano następującą nomenklaturę jeśli chodzi o podstawowe części wykresu:
W pierwszym rozdziale omówiono najczęściej stosowane w biologii nadrzędne funkcje graficzne pod kątem rodzajów wykresów tworzonych w polu kreślenia. Kolejne rozdziały pokazują po kolei rozwiązania różnych problemów związanych z dostosowaniem wielkości wykresu, marginesów, wielkości i krojów czcionki, konstrukcji odpowiedniej osi, umiejscowienia podpisów pod osiami itp. Rozwiązania te są uniwersalne i dotyczą wszystkich rodzajów wykresów. Rozdział 10 pokazuje dodatkowe możliwości wynikające z dokładania do wykresu różnych symboli i figur geometrycznych za pomocą podrzędnych funkcji graficznych. Rozdziały powyżej 10 pokazują przykładowe opracowania graficzne wykonywane w badaniach biologicznych. Są przeznaczone do oglądania i kopiowania skryptów w celu ich późniejszej modyfikacji, a także zobaczenia, jak opracowuje się dane biologiczne.
Wybrane nadrzędne funkcje graficzne
Funkcja plot()
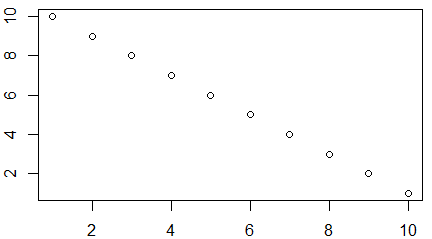
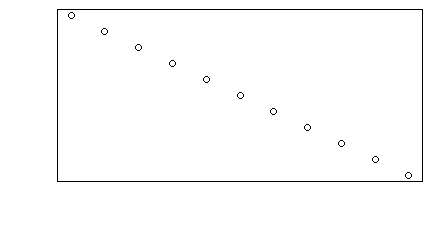
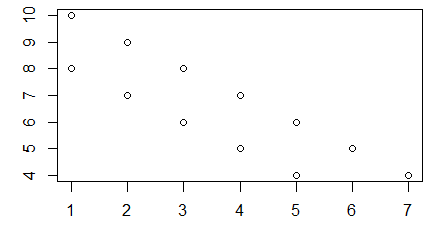
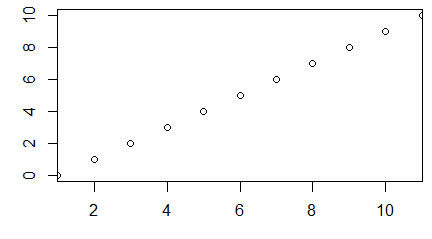
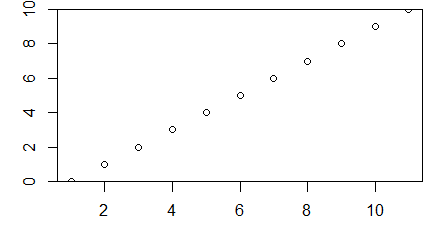
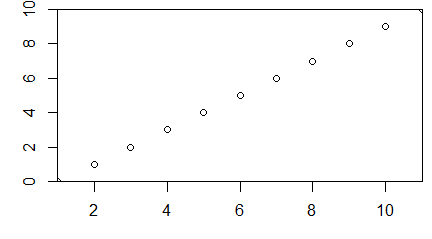
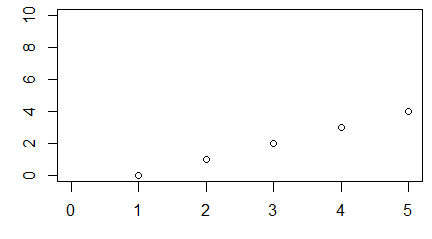
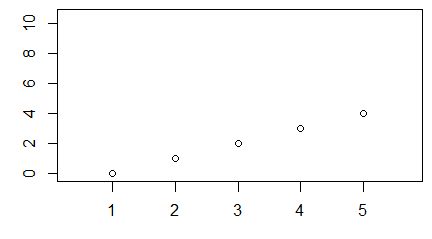
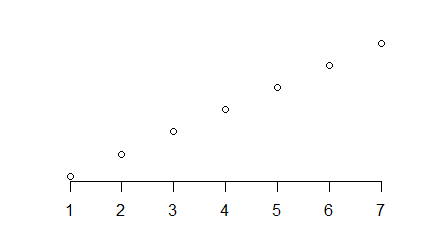
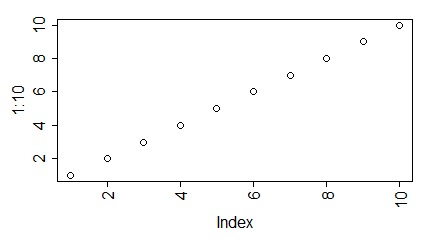
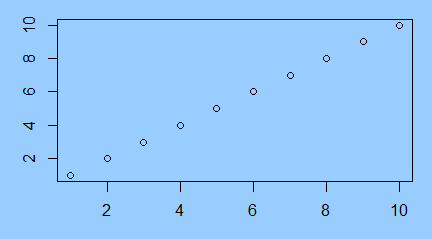
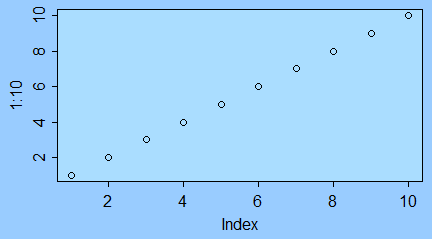
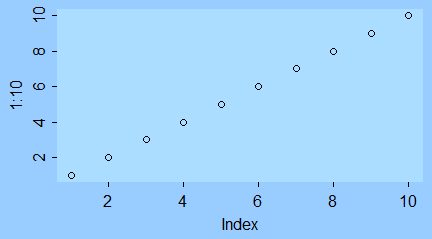
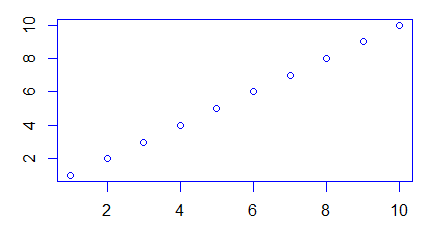
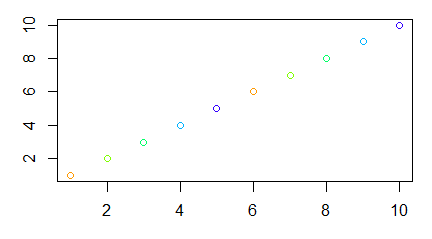
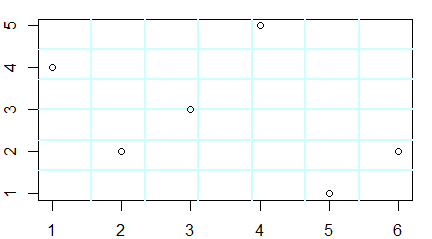
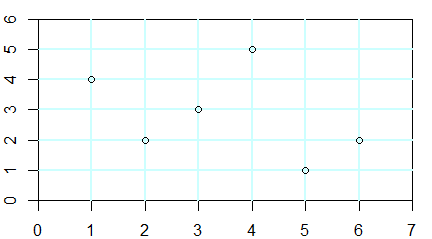
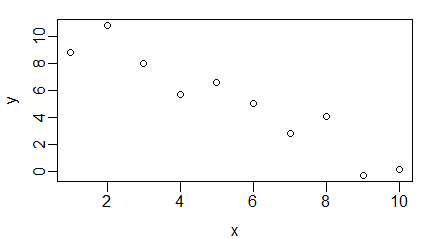
Funkcja plot() służy do zobrazowania danych zapisanych w wektorach, macierzach, szeregach czasowych i bardziej skomplikowanych strukturach, których elementami są wektory. W najprostszej wersji, gdy zastosujemy ją na pojedynczym wektorze x pojawi się wykres pokazujący rozrzut punktów o współrzędnych (i, x[i]).
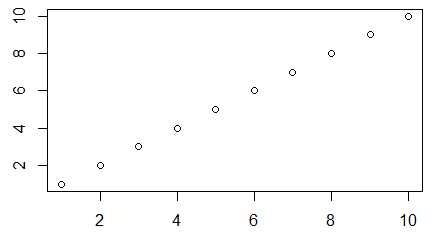
> x=c(850, 950, 700, 550, 900, 650, 650, 800, 30, 700)
> plot(x)
|
Polecenie to powoduje pojawienie się okna graficznego a w nim wykresu rozrzutu punktów o współrzędnych (i, x[i]).
Okno graficzne w R ma swój numer (od 2 w górę) i oznaczenie czy jest aktywne czy nie (ACTIVE/INACTIVE). Można go rozszerzyć na cały ekran lub ściągnąć do paska zadań. Jego wielkość można regulować myszą, z tym, że zbyt małe rozmiary spowodują wygenerowanie komunikatu figure margines to large.
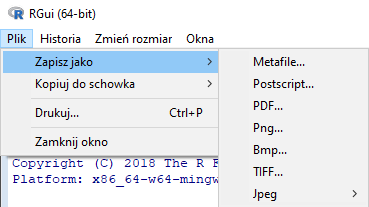
Wykres znajdujący się w oknie graficznym można metodą Ctrl+C, Ctrl+V skopiować do dowolnego pliku graficznego. Można go też zapamiętać w jednym z formatów: Metafile, Postscript, PDF, Png, Bmp, TIFF, Jpeg. Zapisuje się w ten sposób sam wykres bez niebieskich obramowań okna graficznego w R.
Wykresy typu plot() inaczej działają, gdy wprowadzi się do nich ciąg liczbowy a inaczej, gdy działają na obiekcie typu factor.
> x=c(1, 8, 2, 1, 1, 8, 8, 8, 2, 2, 1, 1, 8, 8, 2, 8, 1)
> plot(x)
> plot(factor(x))
|
Jeden po drugim powstają następujące wykresy:
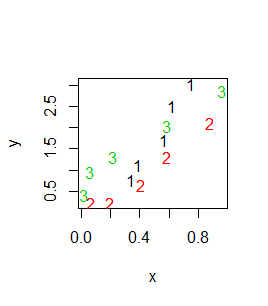
Jeszcze inny typ wykresu powstanie gdy argumentami funkcji plot() są dwa wektory, czynnik i wektor oraz dwa czynniki.
> y=c(850, 950, 700, 550, 900, 650, 650, 800, 650, 700, 600, 850, 900, 750)
> x=c(1, 3, 2, 1, 1, 3, 3, 3, 2, 2, 1, 1, 3, 3)
> plot(x,y)
> plot(factor(x),y)
> plot(factor(x),factor(y))
|
Powstaną kolejno następujące wykresy:
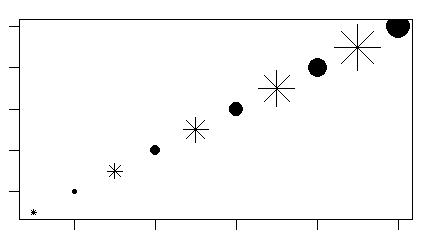
Funkcja plot() służy także do tworzenia wykresów liniowych, punktowo-liniowych, schodkowych, kreskowych za pomocą opcji type=. Wartościami tej opcji są symbole literowe napisane w cudzysłowie.
> x=c(4.84, 1.12, 3.57, 10.57, 0.12, 2.55, 3.10, 3.18, 1.93, 4.15, 7.11,
8.22, 9.96, 0.50, 7.62, 4.33, 7.03, 1.28, 8.42, 1.96)
> plot(x,type="p")
> plot(x,type="l")
> plot(x,type="b")
> plot(x,type="c")
> plot(x,type="o")
> plot(x,type="h")
> plot(x,type="s")
> plot(x,type="S")
> plot(x,type="n")
|
Po kolei powstaną wykresy:
Ostatni typ wykresu przydaje się, gdy chcemy na układ współrzędnych o ustalonym zakresie nałożyć nietypowy rysunek.
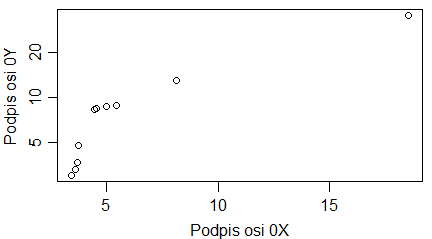
Przy rysowaniu wykresu rozrzutu punktów (x[i],y[i]) można zastosować skalę logarytmiczną o podstawie 10.
> x=c(4.84, 1.12, 3.57, 10.57, 0.12, 2.55, 30.10, 30.18, 100.93, 400.15)
> y=c(0.77, 0.13, 0.71, 0.51, 0.04, 0.82, 1.70, 2.80, 10.37, 10.67)
> plot(x, y)
> plot(x, y, log="x")
> plot(x, y, log="y")
> plot(x, y, log="xy")
|
Powstaną kolejno następujące wykresy:
Funkcja matplot()
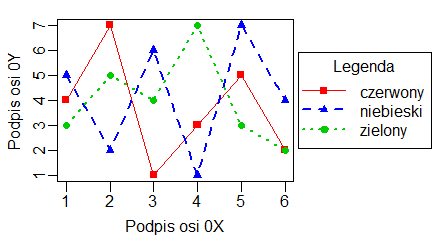
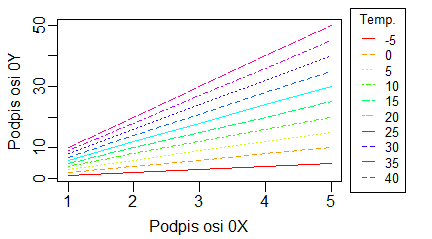
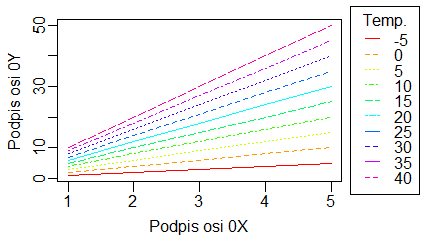
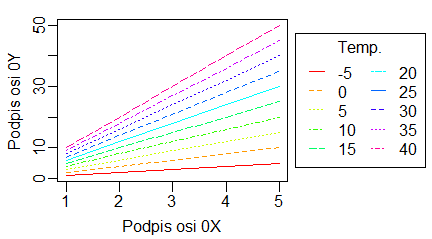
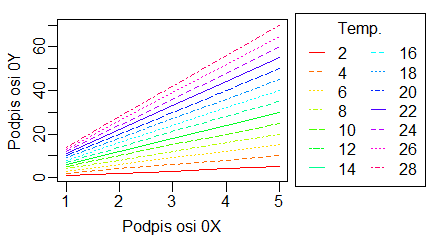
Nierzadko w biologii wykonuje się pomiary zmiennej Y przy określonych z góry wartościach zmiennej X. Jeżeli tego typu eksperyment powtarza się w kilku wariantach (ale dla takich samych wartości zmiennej X) to uzyskane wyniki można zapisać w macierzy. Zobrazowanie tych wyników w postaci punktów o różnych kolorach lub znacznikach, albo różnych linii najwygodniej wykonać za pomocą funkcji matplot().
> temp=c(10, 15, 20, 25, 30)
> y1=c(0.77, 1.13, 1.71, 2.51, 3.04)
> y2=c(0.22, 0.23, 0.65, 1.32, 2.11)
> y3=c(0.41, 0.95, 1.32, 2.03, 2.86)
> y=cbind(y1,y2,y3)
> matplot(temp, y)
> matplot(temp, y, pch=20)
> matplot(temp, y, type="l")
|
Powyższe polecenia spowodowały powstanie po kolei dwóch wykresów:
Standardowo funkcja matplot() w miejsce wartości stawia numer kolumny, z której pochodzą dane. Opcja pch= o wartościach od 1 do 20 w miejsce to stawia znacznik o określonym kształcie. Opcja type= może mieć wartości “p”,”l”,”b”,”c”, “o”, “h”, “s”, “S”, “n” i zmienia typ wykresu tak samo jak w funkcji plot().
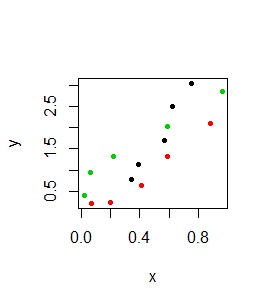
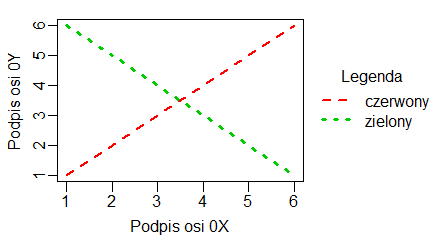
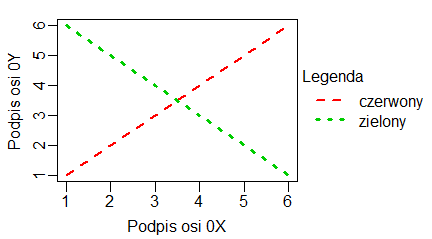
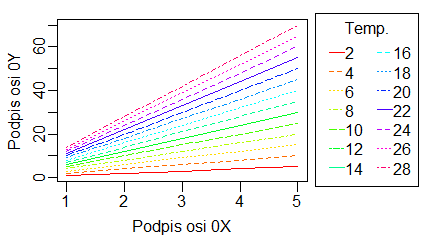
Jeżeli mierzymy dla tych samych obiektów dwie zmienne X i Y (np. długość i masę) a obiekty pochodzą z trzech populacji statystycznych wartości zmiennej X możemy zapisać w jednej macierzy, a zmiennej Y w drugiej. Wtedy funkcja matplot() odpowiednio przyporządkowuje dane do siebie.
> x
x1 x2 x3
[1,] 0.34 0.07 0.02
[2,] 0.39 0.20 0.06
[3,] 0.57 0.41 0.22
[4,] 0.62 0.59 0.59
[5,] 0.75 0.88 0.96
> y
y1 y2 y3
[1,] 0.77 0.22 0.41
[2,] 1.13 0.23 0.95
[3,] 1.71 0.65 1.32
[4,] 2.51 1.32 2.03
[5,] 3.04 2.11 2.86
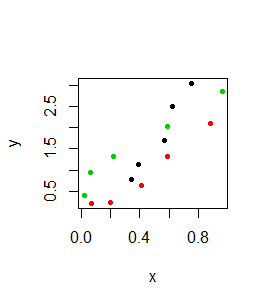
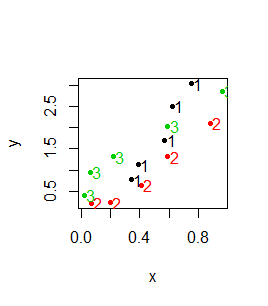
> matplot(x, y)
> matplot(x, y, pch=20)
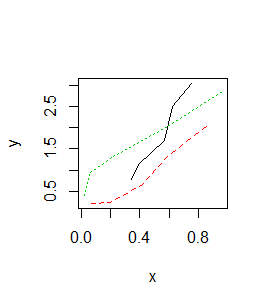
> matplot(x, y, type="l")
|
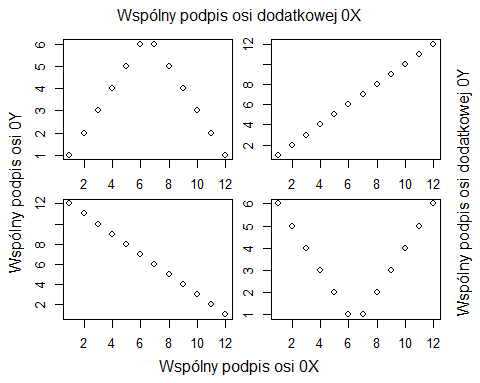
Powyższe polecenia spowodują powstanie po kolei następujących wykresów:
Z funkcją graficzną matplot() współdziałają funkcje graficzne dokładające matpoints() oraz matlines(). Pierwsza z nich dokłada do wykresu numer kolumny, z której pochodzą dane, druga dokłada linie do wykresu, w którym występują liczby.
> x
x1 x2 x3
[1,] 0.34 0.07 0.02
[2,] 0.39 0.20 0.06
[3,] 0.57 0.41 0.22
[4,] 0.62 0.59 0.59
[5,] 0.75 0.88 0.96
> y
y1 y2 y3
[1,] 0.77 0.22 0.41
[2,] 1.13 0.23 0.95
[3,] 1.71 0.65 1.32
[4,] 2.51 1.32 2.03
[5,] 3.04 2.11 2.86
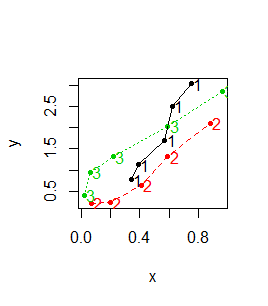
> matplot(x, y, pch=20)
> matpoints(x+0.05,y)
> matlines(x,y)
|
Pierwszy z pokazanych wykresów przechodzi na drugi, a drugi na trzeci:
Funkcja matplot() działa na odpowiadających sobie wektorach lub macierzach. Działa także gdy odpowiadające sobie wektory są zapisane w typie data.frame, choć z formalnego punktu widzenia nie są to bazy danych (baza danych miałaby jedna kolumnę będącą czynnikiem, która pokazywałaby do jakiej kategorii należą dane i tylko jedną kolumnę na wartości zmiennej X i jedna kolumnę na wartości zmiennej Y).
Funkcja curve()
Funkcje plot() i matplot() z opcją type=”l” umożliwiły robienie wykresów liniowych. Wykresy liniowe stosuje się do obrazowania wszelkich funkcji matematycznych jednej zmiennej. Zastosowanie wymienionych funkcji graficznych wymagałoby wyliczenie najpierw wektora wartości x dla jakich wyliczone będą wartości funkcji f(x) zapisane w drugim wektorze y, a następnie wykonanie funkcji plot(x,y,type=”l”). Działania te skraca funkcja graficzna curve() o specjalnej składni:
curve(nazwa_funkcji, from=x_min, to=x_max)
Domyślnie x_min=0 i x_max=1.
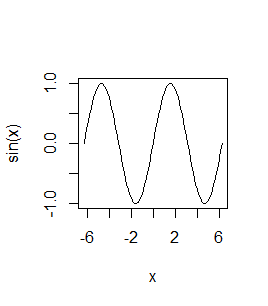
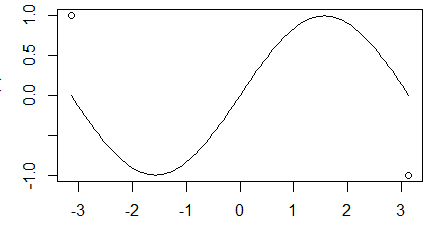
> curve(sin)
> curve(sin,-2*pi,2*pi)
|
Po kolei powstaną dwa wykresy:
Takie same wykresy powstaną gdy zastosujemy składnię curve(sin(x)) oraz curve(sin(x),-2*pi, 2*pi). Składnię ze wskazaniem argumentu należy stosować gdy w miejscu funkcji zastosuje się działania matematyczne (np. 10*sin(x)). Ponadto funkcja ta ma opcję logiczną add= mającą standardowo wartość FALSE. Kiedy zmienimy ją na TRUE powstanie funkcja graficzna dokładająca. Umożliwia to narysowanie kilku funkcji matematycznych na jednym wykresie.
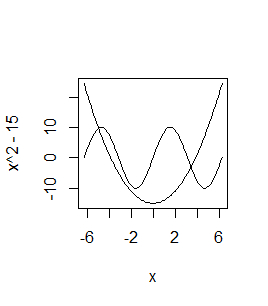
> curve(x^2-15,-2*pi,2*pi)
> curve(10*sin(x),add=TRUE)
|
Spowoduje to powstanie następującego wykresu:
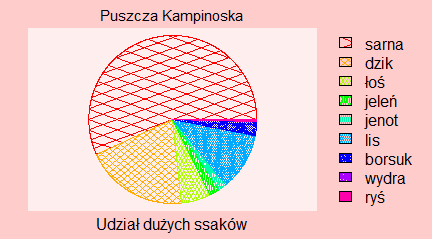
Funkcja pie()
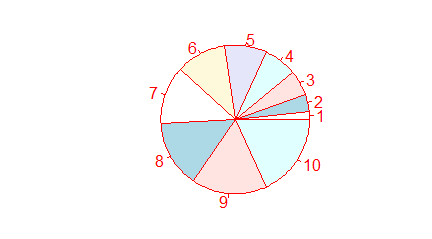
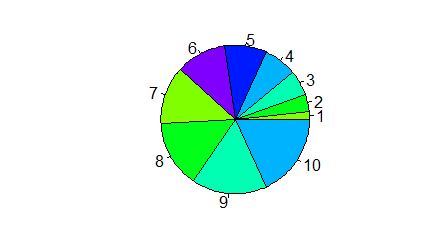
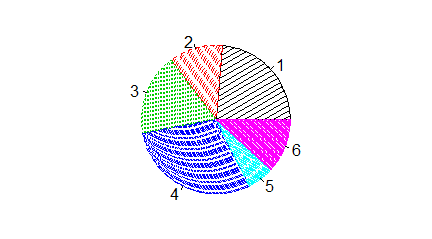
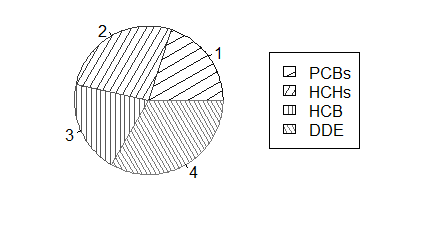
Jeżeli w jednym zgrupowaniu zakwalifikujemy obiekty do kilku kategorii zwyczajowo podaje się procent obiektów należących do pierwszej, drugiej, n-tej kategorii. Jednym z najpopularniejszym sposobem obrazowania wyników takich badań jest podział koła na części o powierzchni proporcjonalnej do procentu obiektów należących do danej kategorii. W R służy do tego funkcja pie(). Jest to funkcja, która odpowiedni procent sama wylicza dla dowolnego ciągu.
> N=c(10,11,22,18)
> proc=N/sum(N)*100
> pie(N)
> pie(proc)
|
Kolejno pojawiające się wykresy są identyczne.
Funkcja pie() nie działa na czynnikach, natomiast na szeregach czasowych działa tak samo, jak na wektorach, z których ten szereg został utworzony.
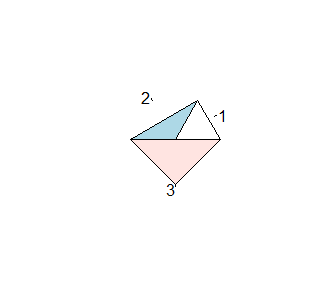
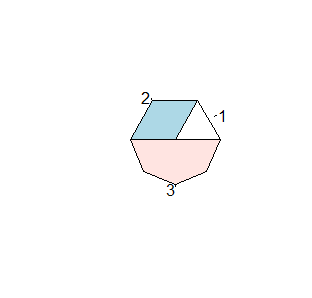
Niektóre opcje funkcji pie() zmieniają istotnie kształt wykresu. Może być to wielokąt z dodanymi punktami wyznaczonymi przez końce odcinków wychodzących z jednego punktu i kątach między nimi proporcjonalnych do wartości wyrazów wektora. Ustala się to za pomocą opcji edge=x, gdzie x ma domyślną wartość 200.
| > x=c(1,2,3) > pie(x, edge=1) > pie(x, edge=6) > pie(x, edge=10) > pie(x, edge=20) |
Powstałe w ten sposób figury nie specjalnie nadają się do obrazowania wyników badań.
Wykres kołowy wydaje się bardzo niewielki na tle całego wykresu a odpowiada za to domyślna opcja radius=x mająca wartość 0.8. Ustawienie jej na 1 całkowicie wypełnia pole kreślenia, a większa wartość powoduje, że figura nie mieści się w polu kreślenia.
> x=c(1,2,3)
> pie(x)
> pie(x, radius=1)
> pie(x, radius=1.5)
|
Powstaną w ten sposób kolejno trzy wykresy:
Opcja logiczna clockwise określa kierunek, w jakim przyporządkowywane są wycinkom koła odpowiednie wartości. Standardowo jest to kierunek przeciwny do ruchu wskazówek zegara i można to zmienić wpisując clockwise=TRUE. Z kolei opcja init.angle=x określa kąt nachylenia promienia, od którego rozpoczyna się wykres, do osi 0X. Kąt ten wyrażany jest w stopniach.
> x=c(4,2,3,4)
> pie(x)
> pie(x, clockwise=TRUE)
> pie(x, clockwise=TRUE, init.angle=0)
|
Spowoduje to powstanie kolejno trzech wykresów.
Funkcja ta nie ma więcej możliwości graficznych, np wysuwania nieco wyróżnionego odcinka koła, patrzenia na wykres kołowy pod kątem (zmienia się on wtedy w elipsę). Tego typu możliwości (bardziej potrzebne do wizualizacji danych na posterach lub prezentacjach, niż w pracy naukowej) można uzyskać dopiero w dodatkowych pakietach graficznych.
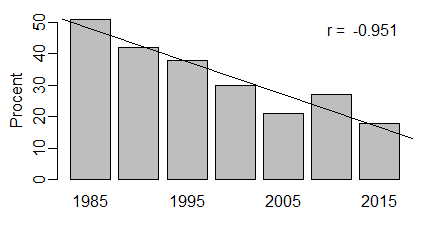
Funkcja barplot()
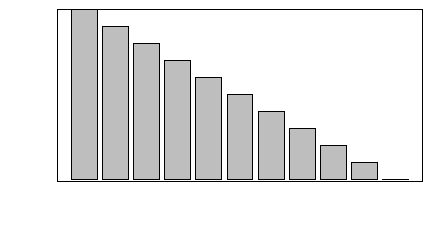
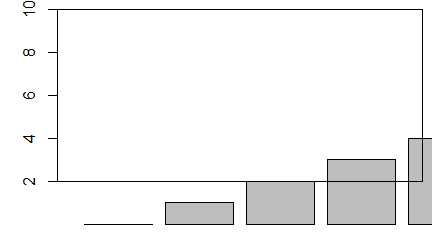
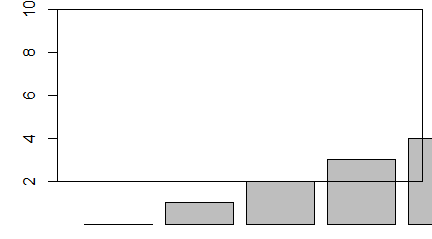
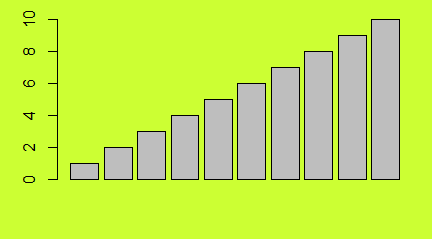
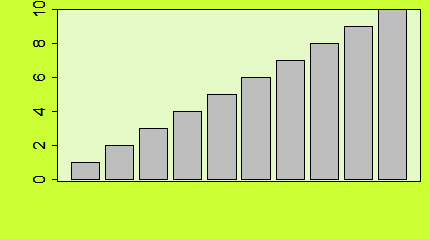
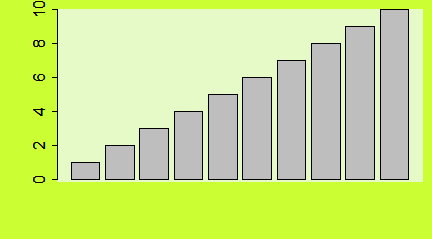
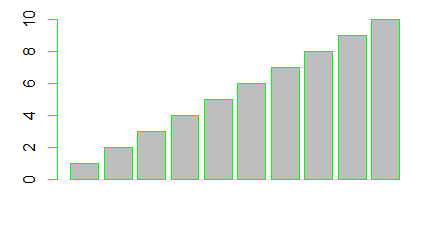
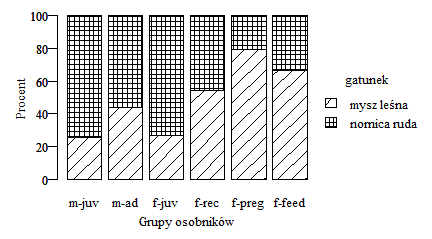
Liczbę lub procent wyróżnionych obiektów w różnych zgrupowaniach zazwyczaj pokazuje się na wykresach słupkowych. Gdy dysponujemy tego typu danymi, możemy wykonać wykres słupkowy używając funkcji barplot()
> N=c(123, 67, 93)
> A=c(32, 15,12)
> proc=A/N*100
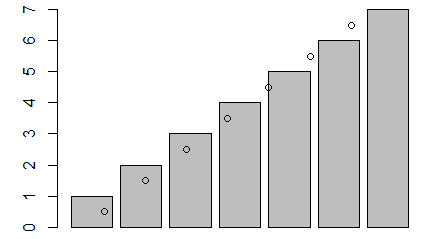
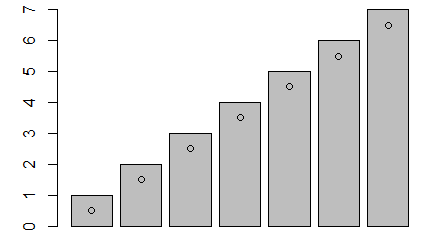
> barplot(N)
> barplot(A)
> barplot(proc)
|
Kolejno powstaną następujące wykresy:
Dla wektora liczbowego funkcja barplot() tworzy szereg słupków o wysokości określonej przez podane liczby. Ich interpretacja zależy od sposobu przygotowania danych.
Funkcja barplot() działa także na macierzach liczbowych. Tworzy wtedy słupki o wysokości równej sumie liczb w poszczególnych kolumnach, których części o długości równej poszczególnym liczbom w kolumnach są inaczej zaciemnione.
> mat=matrix(1:12,3,4)
> mat
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12
> barplot(mat)
> mat1=matrix(1:12,3,4,byrow=TRUE)
> mat1
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 5 6 7 8
[3,] 9 10 11 12
> barplot(mat1)
|
Kolejno powstaną dwa wykresy:
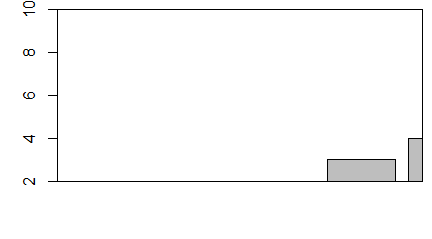
Opcja logiczna beside=TRUE powoduje, że części słupków związane z daną liczbą w macierzy są zestawiane obok siebie.
> mat=matrix(1:12,3,4)
> mat
> barplot(mat, beside=TRUE)
> mat1=matrix(1:12,3,4,byrow=TRUE)
> barplot(mat1,beside=TRUE)
|
Wykresy, które teraz powstaną wyglądają następująco:
Funkcja barplot() umożliwia także robienie wykresów słupkowych ułożonych poziomo. Służy do tego opcja logiczna horiz=, która standardowo ma wartość domyślna FALSE. Po zmianie jej wartości na TRUE powstanie wykres o orientacji poziomej.
> x=1:4
> barplot(x,horiz=TRUE)
> xx=cbind(1:4,2:5,3:6)
> barplot(xx,horiz=TRUE)
> barplot(xx,horiz=TRUE,beside=TRUE)
|
Spowoduje to powstanie następujących wykresów:
Argumentem funkcji barplot nie może być czynnik ani szereg czasowy.
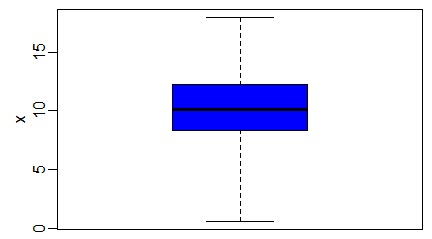
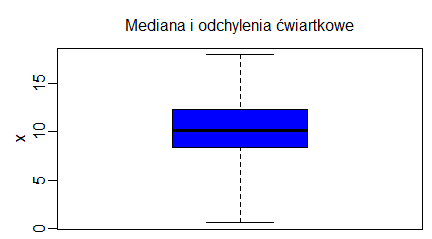
Funkcja boxplot()
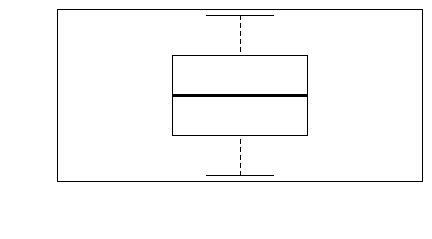
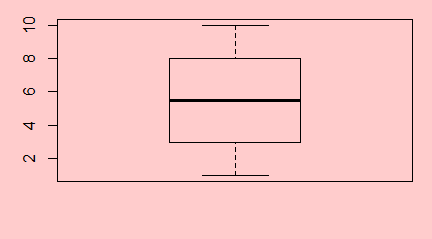
W Excelu, z braku możliwości zrobienia wykresu pudełkowego, średnie lub mediany wartości jakiejś zmiennej ciągłej wyliczonej w kilku zgrupowaniach wraz z odchyleniami standardowymi, odchyleniami ćwiartkowymi rysuje się na wykresach słupkowych. Wykres pudełkowy znacznie lepiej oddaje ideę średniej, która nie musi zaczynać się od 0 i może mieć wartości ujemne (np. dla temperatury w °C). W R wykresy tego typu tworzy się za pomocą funkcji boxplot(). W przeciwieństwie do funkcji barplot() jest to funkcja nie tylko rysująca wykres, ale przeliczająca dane.
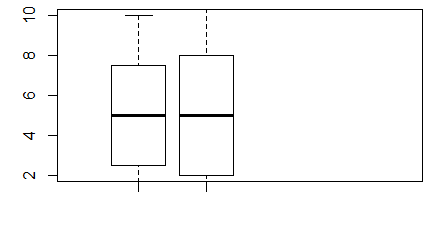
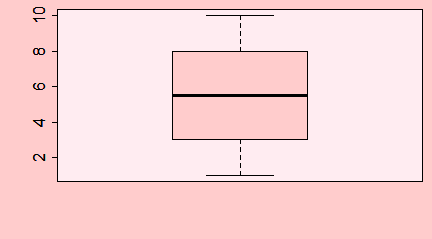
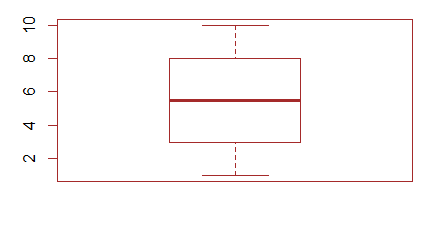
> x=1:20
> y=1:40
> boxplot(x,y)
|
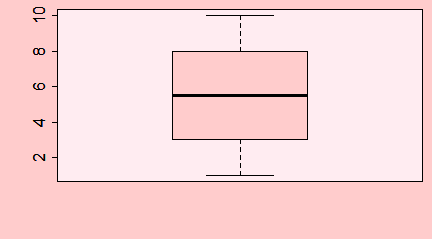
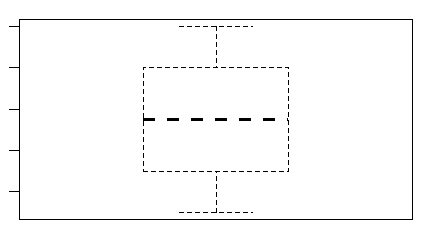
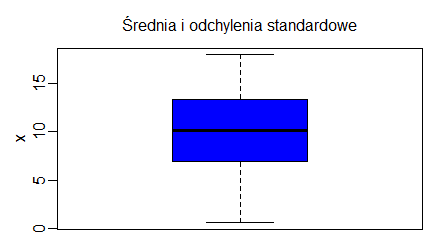
Spowoduje to powstanie wykresu wyglądającego następująco:
Centralną część pudełka zajmuje mediana ciągu, dolny koniec pudełka to pierwszy kwartyl, górny koniec to trzeci kwartyl, dolny koniec centralnej kreski to wartość minimalna wektora, a jej górny koniec to wartość maksymalna. Wszystkie te wielkości wyliczono osobno dla pierwszego i drugiego wektora i, co więcej, wektory te nie muszą być jednakowej długości.
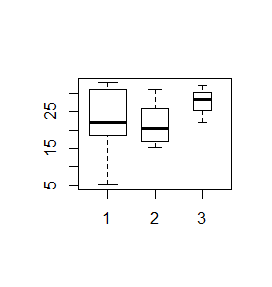
Rzeczywiste dane rzadko kiedy mają regularnie zmieniające się wartości. Często pojawiają się wartości odbiegające od pozostałych. Funkcja boxplot() ocenia czy dane mieszczą się w obszarze wyznaczonym przez iloczyn odległości międzykwartylowej oraz liczbę określoną przez opcję range=x. Opcja ta ma domyślną wartość 1.5. Odbiegające dane, nie mieszczące się w wyznaczonym obszarze, są umieszczane jako osobne kółeczka, a ekstrema, zaznaczone jako końce centralnej kreski, są wyznaczane dla pozostałych danych.
> x=c(0.03, 31.49, 18.49, 22.23, 32.96, 26.48, 31.58,
21.26, 24.64, 34.69)
> y=c(29.97, 20.35, 18.44, 51.17, 2.00, 15.33, 15.36)
> boxplot(x,y)
> boxplot(x,y,range=2)
> boxplot(x,y,range=3)
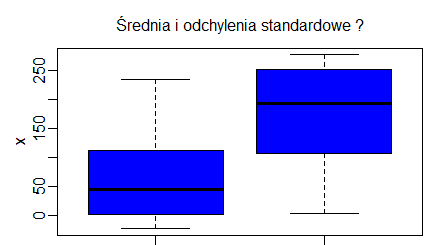
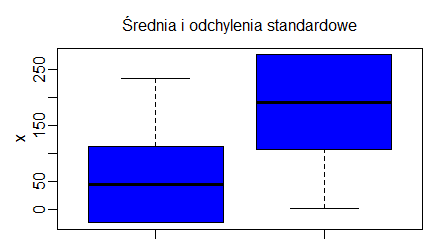
|
Daje to następujące wykresy.
Nadanie opcji range= wartości 0 powoduje, że wszystkie dane są uwzględniane przy wyliczaniu końców centralnej kreski.
Opcja width=c(n1,n2,..,nk) określa względne szerokości kolejnych pudełek. Jej odmiana, opcja logiczna varwidth=TRUE powoduje, że szerokości pudełek będą proporcjonalne do wielkości prób, z których wyliczana jest mediana.
> x=c(5.03, 31.49, 18.49, 12.23, 32.96, 26.48, 31.58, 21.26,
24.64, 14.69, 21.3, 22.8, 31.2, 19.7)
> y=c(29.97, 20.35, 18.44, 51.17, 22.00, 15.33, 15.36)
> z=c(22.1, 32.3, 28.5)
> boxplot(x,y,z)
> boxplot(x,y,width=c(3,2,1))
> boxplot(x,y,varwidth=TRUE)
|
Spowoduje to wygenerowanie kolejno trzech wykresów.
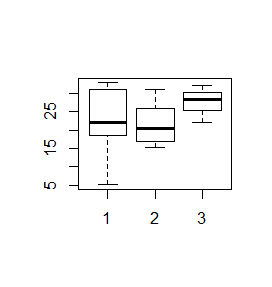
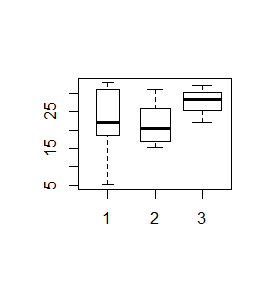
Analizy statystyczne dla porównania median spowodowały, że zaczęto rysować pudełka wcięte. Wcięcia są obliczane za pomocą specjalnej procedury statystycznej wyjaśnionej w podręczniku John M. Chambers, William S. Cleveland, Paul A. Tukey, Beat Kleiner (1983) Graphical Methods for Data Analysis. Duxbury Press, na stronie 62. Wynika z nich, że jeżeli wcięcia dwóch pudełek nie zachodzą na siebie to mediany dwóch rozkładów istotnie różnią się od siebie. Wyjaśnienie tej terminologii będzie miało miejsce na statystyce, natomiast by uzyskać pudełka wcięte w R wystarczy do funkcji boxplot() dodać opcję logiczną notch=TRUE.
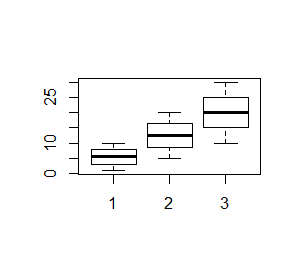
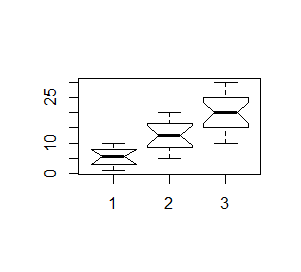
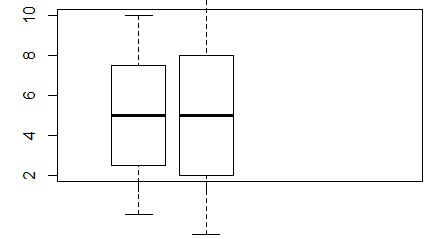
> x=1:10
> y=5:20
> z=10:30
> boxplot(x,y,z)
> boxplot(x,y,z, notch=TRUE)
|
Powstaną kolejno dwa wykresy:
Składnię funkcji boxplot() dostosowano także do tego, by działała na bazach danych. Wtedy istnieje kolumna z danymi i kolumna pokazująca, do której kategorii należą dane. Należy wtedy zastosować składnię:
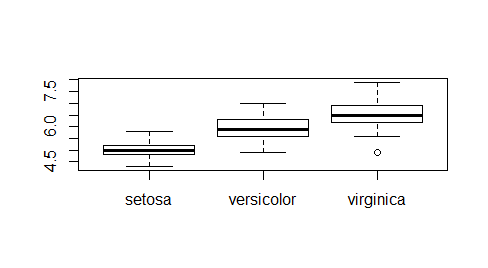
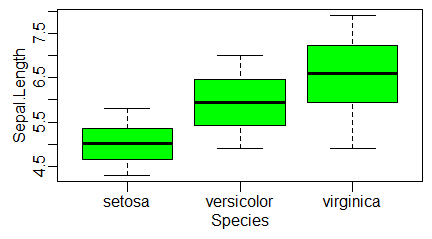
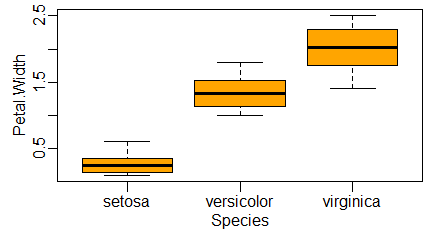
boxplot(nazwa_zmiennej ~ nazwa_czynnika, nazwa_bazy) Przykładowo dla bazy iris zaimplementowanej do R, zmienną, której mediany liczymy, może być Sepal.Length, a czynnikiem Species. Można napisać polecenie:
> boxplot(Speal.Length ~ Species, iris)
|
i uzyskać następujący wykres:
Wszystkie pokazane wykresy można uzyskać w postaci poziomej stosując opcję horiz=TRUE
Funkcja boxplot() poza tym, że rysuje wykres, tworzy także listę obiektów z danymi, które można ewentualnie wykorzystać do innych celów. Aby zobaczyć tę listę należy funkcję tę przyporządkować jakiemuś literałowi, a następnie wywołać ją poprzez literał.
> ir = boxplot(Speal.Length ~ Species, iris)
> ir
$stats
[,1] [,2] [,3]
[1,] 4.3 4.9 5.6
[2,] 4.8 5.6 6.2
[3,] 5.0 5.9 6.5
[4,] 5.2 6.3 6.9
[5,] 5.8 7.0 7.9
#
$n
[1] 50 50 50
#
$conf
[,1] [,2] [,3]
[1,] 4.910622 5.743588 6.343588
[2,] 5.089378 6.056412 6.656412
#
$out
[1] 4.9
#
$group
[1] 3
#
$names
[1] "setosa" "versicolor" "virginica"
|
Macierz będąca pierwszym elementem tej listy to podstawowe charakterystyki statystyczne służące do utworzenia pudełek (ekstrema, kwartyle i mediany). Druga macierz będąca elementem listy o nazwie conf to początki i końce ewentualnych wcięć w pudełkach, które można wywołać opcją notch=TRUE.
Funkcja hist()
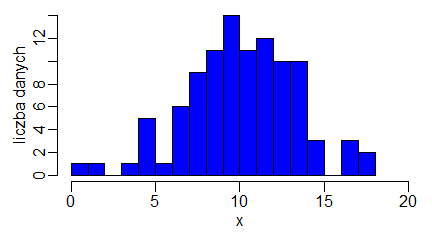
Histogramy są graficznym obrazem tego, co w statystyce nazywane jest rozkładem z próby (ang. sample distribution). Możemy go utworzyć za pomocą funkcji hist(). Jej przydatność wynika stąd, że sama wykonuje wszelkie obliczenia pozwalające na utworzenie takiego wykresu.
>
x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69,
29.73, 22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70,
12.00, 23.35, 2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90)
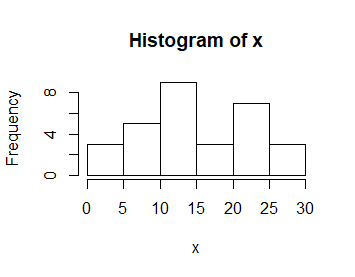
> hist(x)
|
Polecenie to powoduje uaktywnienie się okienka graficznego, w którym został automatycznie stworzony wykres słupkowy.
Wysokość słupków pokazuje jakie jest zagęszczenie liczb w przetwarzanym ciągu w przedziale będącym podstawą słupka. Aby wszystko było jasne przedstawiam nomenklaturę stosowaną przy opracowaniu danych. Jeżeli N jest liczbą wszystkich danych, a N(x1,x2] liczbą danych należących do przedziału (x1,x2] to:
N(x1,x2] jest liczebnością,
N(x1,x2]/N jest frakcją albo prawdopodobieństwem,
N(x1,x2]/N*100 jest procentem,
N(x1,x2]/(x2-x1) jest zagęszczeniem,
N(x1,x2]/(N*(x2-x1)) jest intensywnością (gęstością) prawdopodobieństwa.
Funkcja hist() tworzy standardowo wykresy liczebności danych i suma wysokości wykreślonych słupków jest równa liczbie wszystkich obiektów. Natomiast najlepszą interpretację w odniesieniu do rzeczywistości mają wykresy intensywności prawdopodobieństwa. Są one przybliżeniem prawdopodobieństwa z jakim możemy wylosować obiekt o danej wartości zmiennej z całej populacji. Wykres intensywności prawdopodobieństwa uzyskamy stosując jedną z opcji: freq=FALSE albo prob=TRUE.
> x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69, 29.73,
22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70,
12.00, 23.35, 2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90)
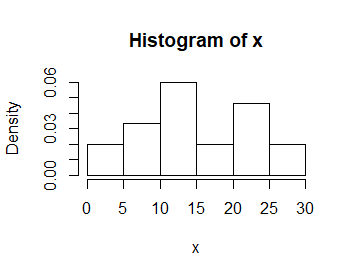
> hist(x, prob=TRUE)
|
Powstały wykres różni się od poprzedniego tylko liczbami na osi pionowej.
W tego typu wykresie suma pół powierzchni wykreślonych słupków jest równa 1.
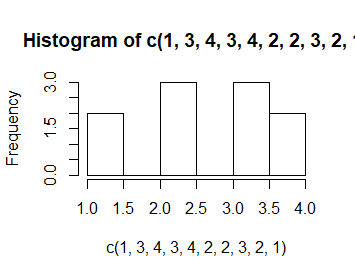
Liczba i długość przedziałów, w których zliczane są dane, jest wyznaczana domyślnie. Nazywa się je przedziałami histogramowania. Domyślnie są to przedziały prawostronnie domknięte, a lewostronnie otwarte (poza pierwszym przedziałem, który jest obustronnie domknięty). Ich granice trzeba ustalić arbitralnie i zazwyczaj robi się to tak, by były to jakieś “okrągłe” liczby. Opcja breaks=c(n1,n2,…,nk) pozwala na sztywne określenie tych granic.
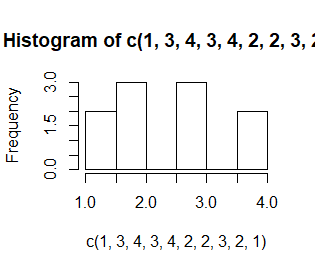
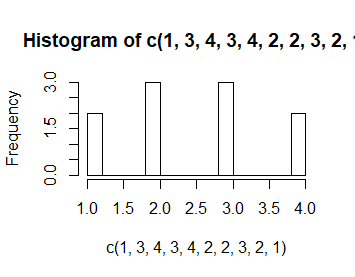
> hist(c(1,3,4,3,4,2,2,3,2,1))
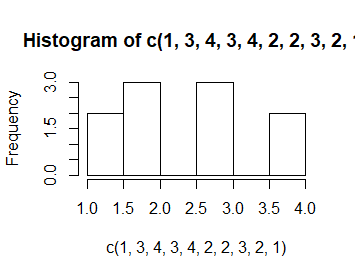
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=c(0.5,1.5,2.5,3.5,4.5))
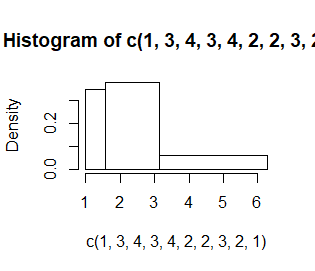
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=c(pi/2, pi, 2*pi))
|
Kolejno powstają zupełnie niepodobne do siebie wykresy mimo, ze dotyczą tych samych danych. Dodatkowo, przy nierównych przedziałach uruchomiła się automatycznie opcja prob=TRUE.
Ta sama opcja, breaks, ale o wartości będącej liczba całkowitą, breaks=n pozwala do pewnego stopnia zmienić liczbę przedziałów histogramowania. Przeszkadza jej w tym tylko algorytm wyznaczania granic tych przedziałów jako ładnych “okrągłych” liczb, co powoduje, że nie działa ona dokładnie.
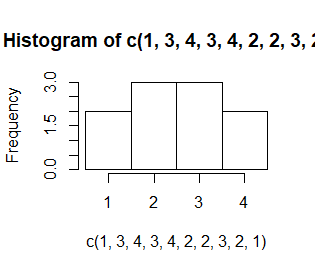
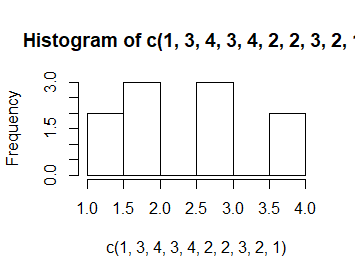
> hist(c(1,3,4,3,4,2,2,3,2,1), breaks=2)
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=3)
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=4)
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=5)
> hist(c(1,3,4,3,4,2,2,3,2,1),breaks=11)
|
Opcja right=FALSE umożliwia stosowanie przedziałów histogramowania lewostronnie domkniętych a prawostronnie otwartych.
> hist(c(1,3,4,3,4,2,2,3,2,1))
> hist(c(1,3,4,3,4,2,2,3,2,1),right=FALSE)
|
Nawet taka mała różnica powoduje zmianę wykresu.
Wszystko to pokazuje, jak wielkie znaczenie ma sposób podziału osi 0X na przedziały histogramowania.
Warto wiedzieć, że wielkości potrzebne do zrobienia histogramu także zapisywane są w liście, którą można zobaczyć, a nawet wykorzystać w różnych operacjach. Gdy zapisze się wykres jako obiekt o danej nazwie, wystarczy popatrzyć co kryje się pod tą nazwą:
> x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69, 29.73,
22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70, 12.00, 23.35,
2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90)
> hist(x)->a
> a
$breaks
[1] 0 5 10 15 20 25 30
#
$counts
[1] 3 5 9 3 7 3
#
$density
[1] 0.02000000 0.03333333 0.06000000 0.02000000 0.04666667 0.02000000
#
$mids
[1] 2.5 7.5 12.5 17.5 22.5 27.5
#
$xname
[1] "x"
#
$equidist
[1] TRUE
#
attr(,"class")
[1] "histogram"
|
Powstaje lista złożona z “breaks” – granic przedziałów histogramowania, “counts” – liczby wartości ciągu w kolejnych przedziałach histogramowania, “density” – intensywności prawdopodobieństwa, “mids” – środkach przedziałów histogramowania i domyślnych wartości podstawowych opcji. Do pokazanych wartości mamy dostęp i możemy ich użyć w innych wykresach. Przykładowo by utworzyć rozkład procentowy, wystarczy zastosować funkcję barplot() do danych a[[2]]/length(x)*100. Można wręcz napisać polecenie barplot(hist(x)[[2]]/length(x)*100)
Podstawowe opcje nadrzędnych funkcji graficznych
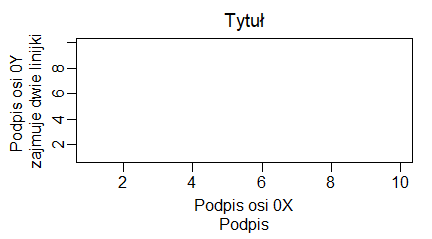
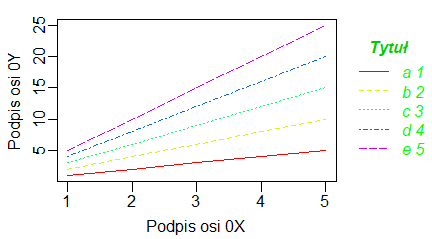
Funkcje graficzne posiadają szereg opcji, które wpisuje się wewnątrz nawiasów okrągłych na zasadzie opcja=… i oddziela przecinkami. Wiele z nich jest jednakowych dla wszystkich przedstawionych funkcji. Umożliwiają zatytułowanie wykresu, podpisanie osi, określenie kolorów i wzorów różnych elementów wykresu i wiele innych rzeczy. Najbardziej potrzebne na ten moment wydają się opcje związane z utworzeniem tytułu wykresu i podpisów pod osiami, bo to co proponują opcje domyślne funkcji graficznych rysujących jest nie do przyjęcia. Opcje te wyglądają następująco:
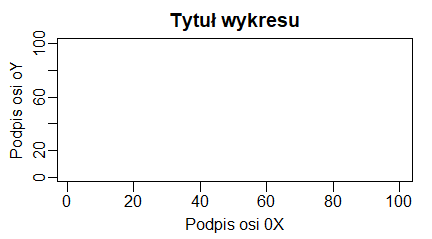
- main=”” Tytuł wykresu napisany na górnym marginesie.
- sub=”” Podpis wykresu napisany na dolnym marginesie.
- xlab=”” Tytuł osi 0X napisany na dolnym marginesie.
- ylab=”” Tytuł osi 0Y napisany na lewym marginesie.
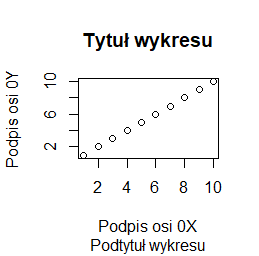
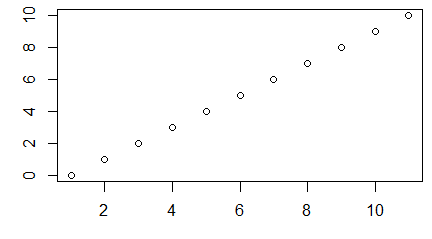
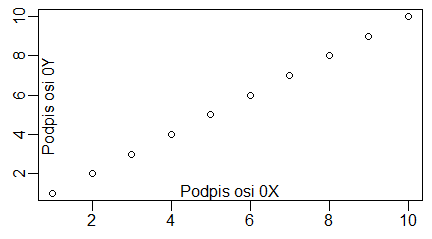
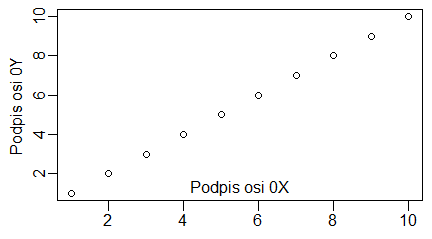
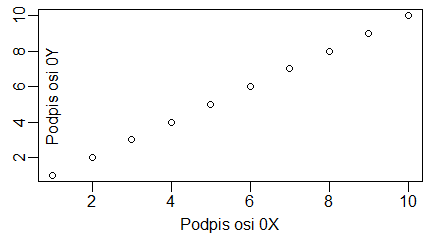
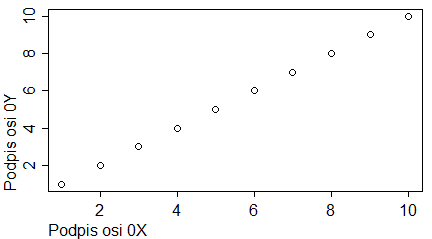
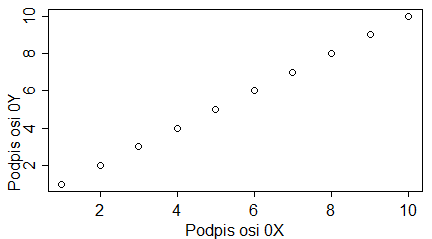
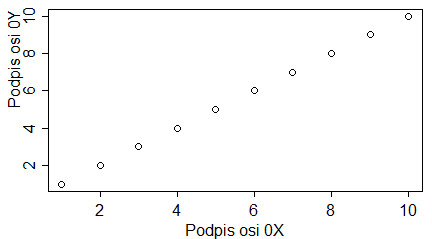
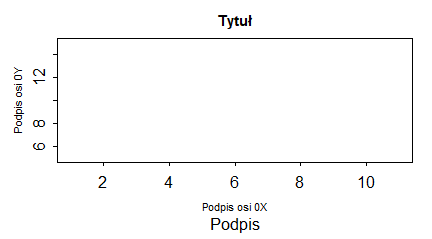
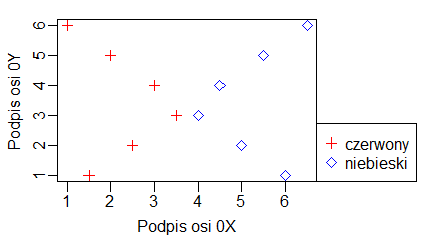
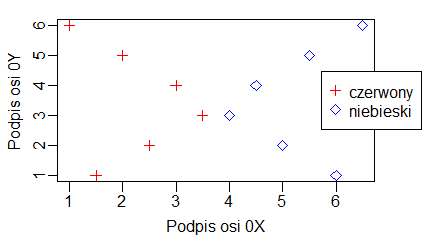
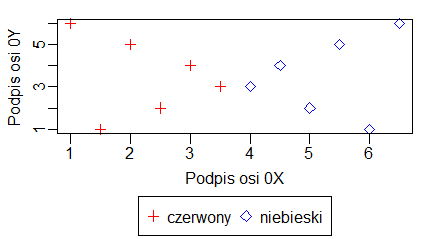
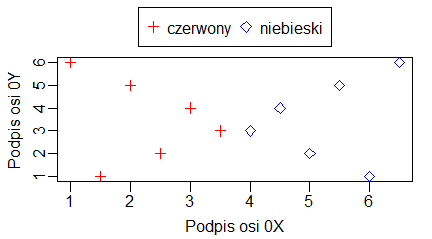
Ich zastosowanie pokazują następujące programy:
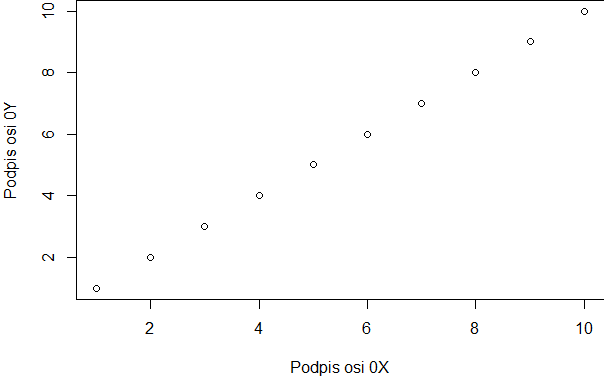
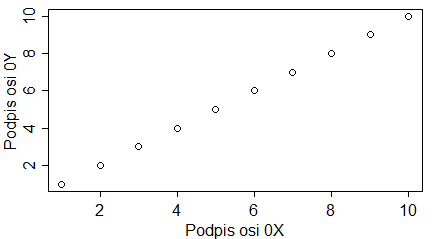
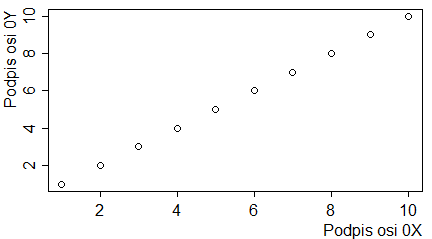
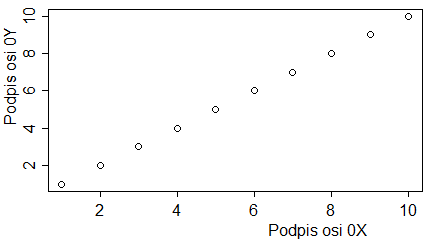
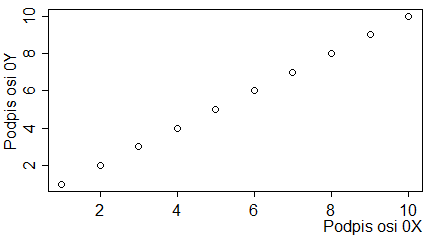
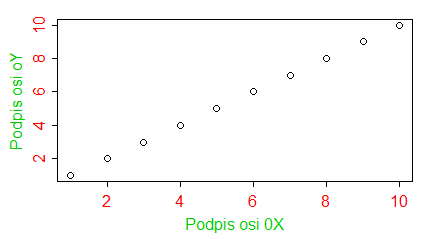
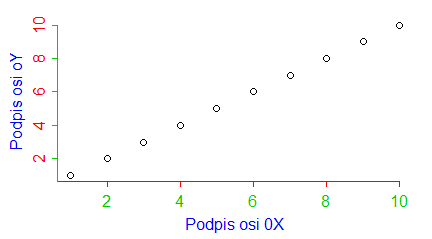
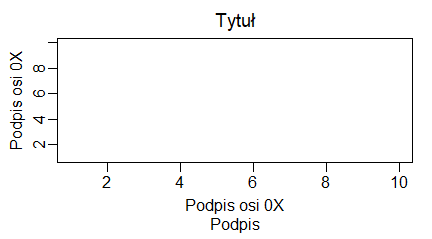
plot(1:10, main="Tytuł wykresu", sub="Podpis wykresu", xlab="Podpis osi 0X", ylab="Podpis osi 0Y") |
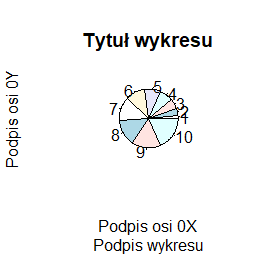
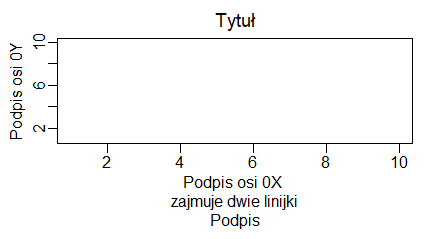
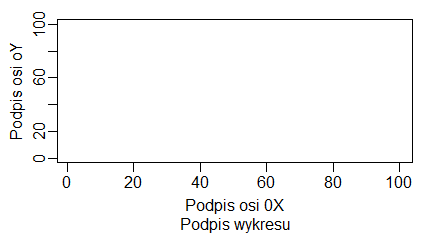
pie(1:10, main="Tytuł wykresu",
sub="Podpis wykresu",
xlab="Podpis osi 0X",
ylab="Podpis osi 0Y")
|
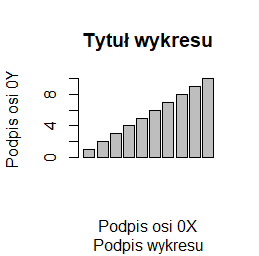
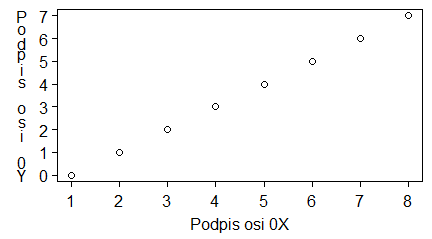
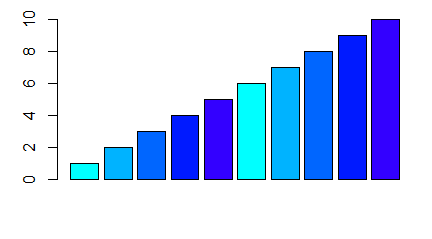
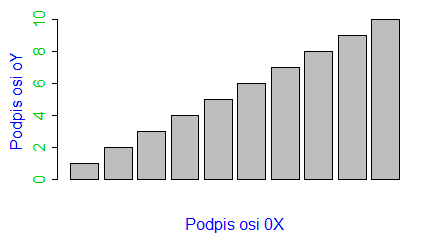
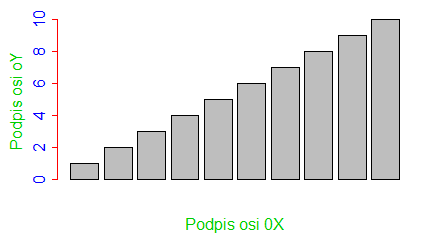
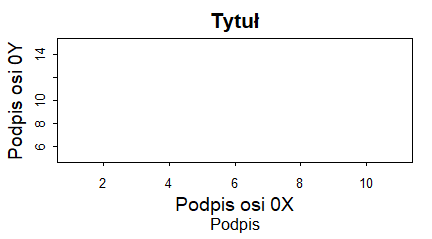
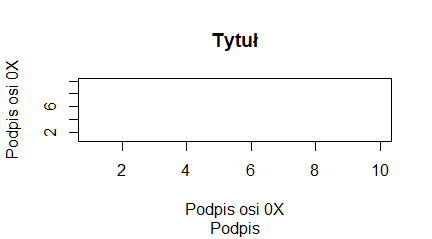
barplot(1:10, main="Tytuł wykresu",
sub="Podpis wykresu",
xlab="Podpis osi 0X",
ylab="Podpis osi 0Y")
|
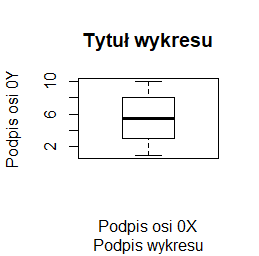
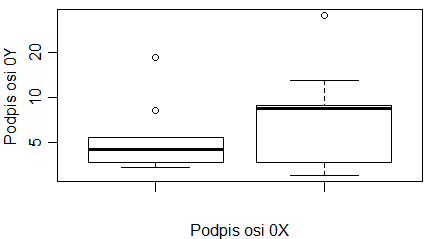
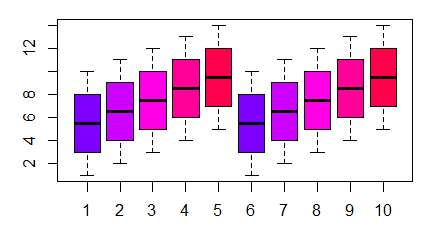
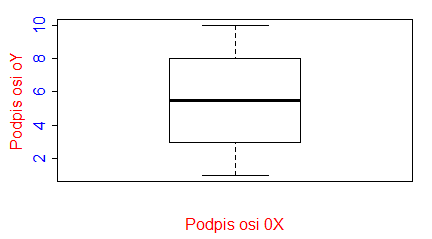
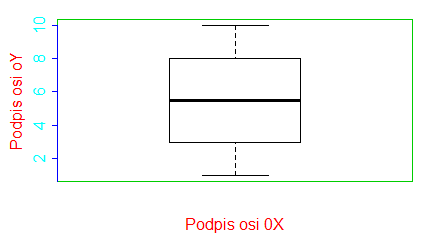
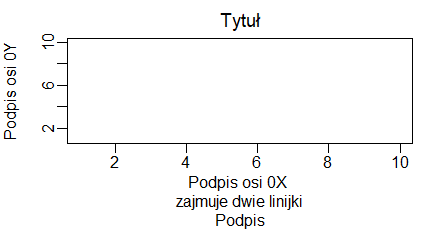
boxplot(1:10, main="Tytuł wykresu",
sub="Podpis wykresu",
xlab="Podpis osi 0X",
ylab="Podpis osi 0Y")
|
Programy te trzeba wykonywać po kolei, by uzyskać cztery następujące wykresy:
Inne opcje modyfikujące wykresy opisywane będą przy okazji opisywania różnych problemów związanych z wykonaniem wykresu. Tu pokazujemy wykaz najczęściej stosowanych:
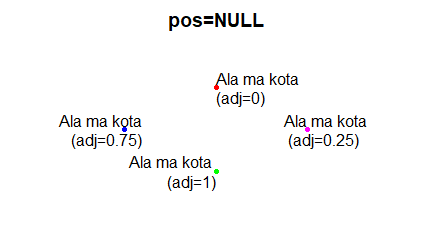
- adj= Sposób wyśrodkowania napisów i podpisów. 0 (z lewej), 0.5 (wyśrodkowane), 1 (do prawej). Może być dowolną liczbą z przedziału [0,1].
- col.main= Kolor tytułu.
- col.sub= Kolor podpisu.
- col.lab= Kolor podpisów osi.
- col= Kolor elementów wykresu.
- ps= Wielkość czcionki.
- xlim=c(a,b) Zakres zmienności danych na osi 0X (od liczby a do liczby b).
- ylim=c(a,b) Zakres zmienności danych na osi 0Y (od liczby a do liczby b).
- pch= Wzór znaczników dla punktów.
- cex= Wielkość znaczników.
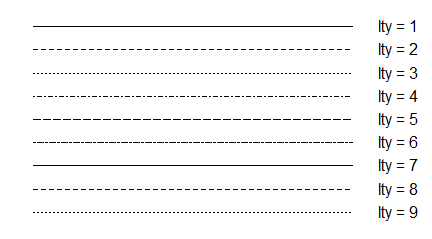
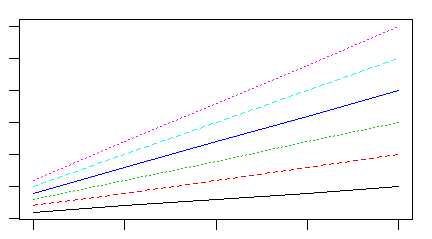
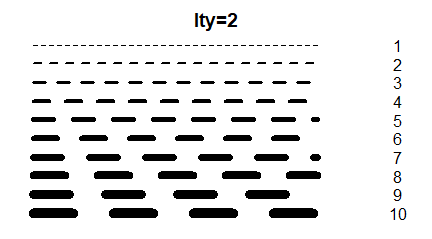
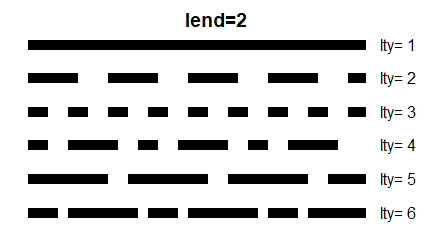
- lty= Typ linii w wykresach liniowych, punktowo liniowych i schodkowych.
- lwd= Grubość linii w wykresach liniowych, punktowo liniowych i schodkowych.
- asp=x Jednostki na osi 0Y w stosunku do jednostek na osi 0X są równe x (dotyczy funkcji plot( ), matplot(), barplot() i curve()).
Nie wyczerpuje to wszystkich opcji stosowanych w funkcjach graficznych. Ich wykaz można zobaczyć po wpisaniu w R polecenia ?Nazwa_funkcji. Pokazuje się strona internetowa z obszernego, oficjalnego podręcznika do programu R. Każda z tych stron ma ujednolicony schemat:
Nazwa biblioteki
|
Nazwa funkcji
|
Usage Formalna bodowa funkcji Alternatywna formalna budowa funkcji ... |
Arguments Wykaz obowiązkowych argumentów i ich typ Wykaz dodatkowych argumentów (parametrów) i ich wartości domyślne |
Details Uwagi dotyczące poszczególnych opcji, ich wartości, związku z innymi funkcjami |
References Literatura opisująca dany rodzaj wykresu, sposób jego zaprogramowania itp. |
See also Linki do powiązanych funkcji |
Examples Przykłady programów |
Formalna budowa funkcji pokazuje formalne nazwy poszczególnych argumentów. Jeżeli pierwszym argumentem jest x, a części “Arguments” znajdujemy informację, że x jest wektorem numerycznym to możemy:
1. Po nazwie funkcji i otworzeniu nawiasu wstawić nazwę wektora numerycznego na pierwszym miejscu.
2. Po nazwie funkcji i otworzeniu nawiasu wstawić x=”nazwa wektora numerycznego” nie koniecznie na pierwszym miejscu.
Podobna zasada dotyczy w R każdej zdefiniowanej funkcji. Przy pisaniu funkcji bez nazw parametrów nalezy stosować taką kolejność wstawiania ich wartości, jaka występuje w formalnej definicji funkcji.
Niekiedy dzięki opcjom nadrzędnych funkcji graficznych powstaje wystarczająco dobry wykres. Jednocześnie wiele elementów uzyskanych dzięki tym opcjom (widok osi, znaczników, podpisy) można nałożyć na wykres poprzez funkcje graficzne podrzędne. Powoduje to, że dalszą część podręcznika skonstruowano na zasadzie wykazu różnych problemów związanych z zaprogramowaniem dobrego wykresu, nie opisów funkcji i ich opcji, jak to zrobiono w tym rozdziale. Niekiedy też informacje powtarzają się, ale w ten sposób łatwiej je znaleźć.
Organizacja okna graficznego
Otwieranie okna graficznego
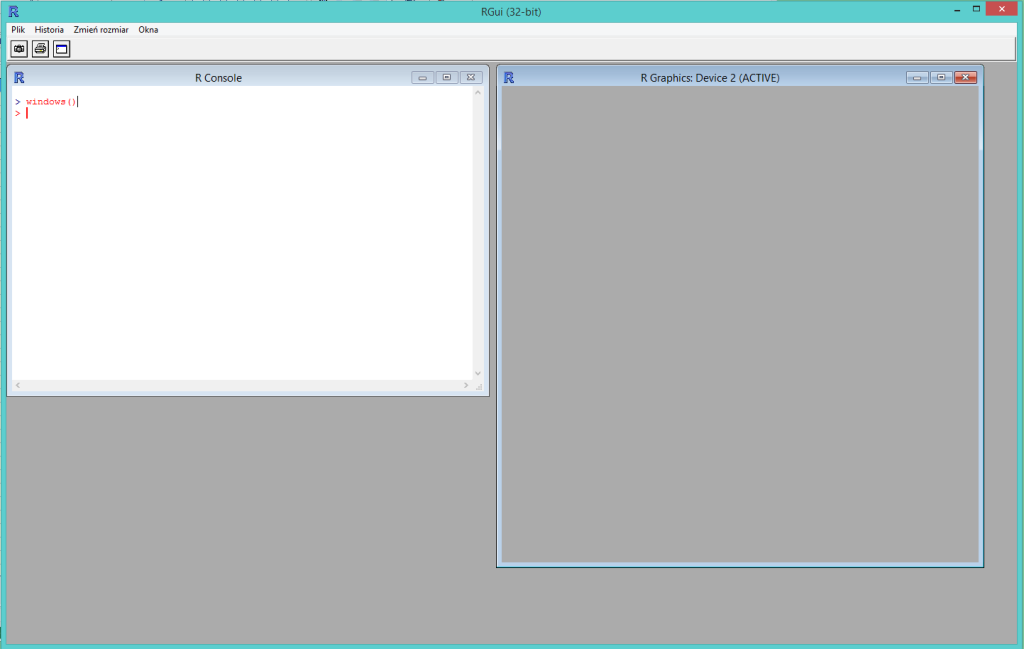
Okna graficzne w systemie windows otwiera się za pomocą funkcji windows(), w systemie Unix/Linux za pomocą funkcji x11(). Jej pierwsze wywołanie spowoduje powstanie okna graficznego z numerem 2 (numer 1 został zarezerwowany na “brak okna graficznego”).
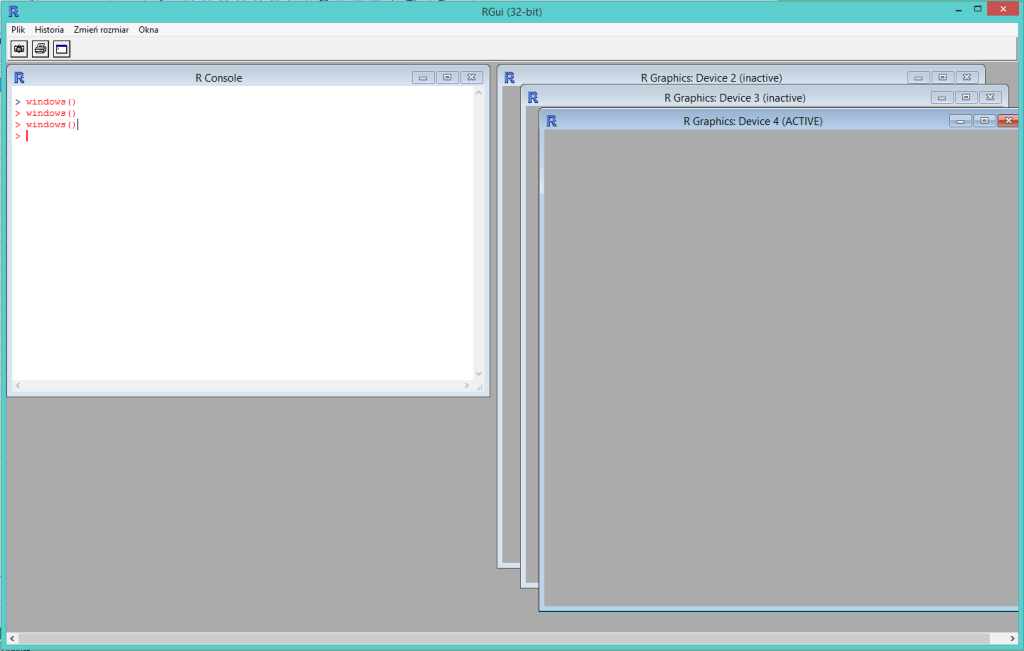
Drugie, trzecie i kolejne wywołania funkcji windows() spowodują powstawanie kolejnych pustych okien graficznych z kolejnymi numerami. Ostatnie wywołane okno będzie aktywne.
Numery otwartych okien graficznych można w każdej chwili pracy z R uzyskać za pomocą funkcji dev.list(). Funkcja dev.cur() pokazuje numer okna aktywnego. Funkcja dev.set(n), gdzie n jest liczba całkowitą, uaktywnia okno o numerze n, o ile jest ono otwarte. Gdy okno o tym numerze nie jest otwarte uaktywnione zostanie pierwsze okno z listy okien otwartych. Funkcja dev.new() spowoduje powstanie nowego okna graficznego o najniższym numerze (ale większym od 2), którego nie ma wśród otwartych okien.
> dev.list()
windows windows windows
2 3 4
> dev.cur()
windows
4
> dev.set(2)
windows
2
> dev.set(1)
null device
1
> dev.new(15)
> dev.new(1)
> dev.new()
> dev.list()
windows windows windows windows windows windows
2 3 4 5 6 7
|
Zamykanie otwartych okien graficznych wykonuje się za pomocą funkcji dev.off(n), gdzie n jest numerem okna, które chcemy zamknąć. Funkcja ta przy tym pokazuje numer okna aktywnego. Wywołanie jej bez numeru powoduje zamknięcie okna aktywnego. Pozostałe numery otwartych okien nie muszą być kolejnymi liczbami, ale można sprawdzić numer otwartego okna poprzedniego do okna n-tego (funkcje dev.prev(n)) i następnego (funkcja dev.next(n)).
> dev.list()
windows windows windows windows windows windows
2 3 4 5 6 7
> dev.off(3)
windows
7
> dev.list()
windows windows windows windows windows
2 4 5 6 7
> dev.set(5)
windows
5
> dev.off()
windows
6
> dev.list()
windows windows windows windows
2 4 6 7
> dev.prev(4)
windows
2
> dev.next(4)
windows
6
|
Podsumowując, funkcje związane z tworzeniem okien graficznych to:
- windows()
- dev.list()
- dev.cur()
- dev.new()
- dev.off()
- dev.set()
- dev.prev()
- dev.next()
Wymiary okna graficznego
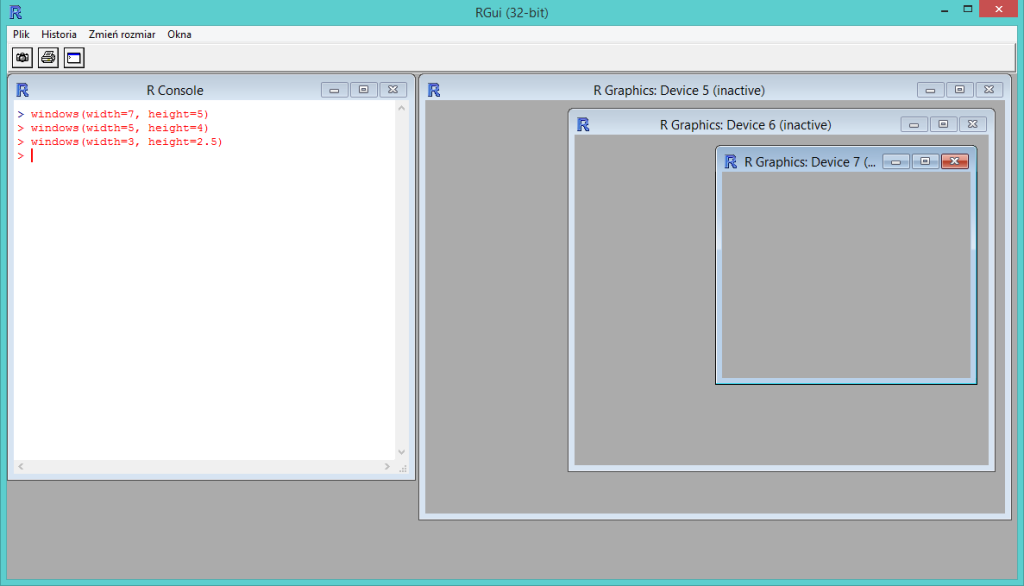
Najważniejszymi opcjami funkcji windows() są width=x1, height=x2 określającymi wielkość tego okna, gdzie x1 i x2 są wyrażone calach. Cal jest ciągle podstawową jednostką miary długości w USA i Wielkiej Brytanii równą 2.54 cm. Funkcja windows() bez opcji otwiera standardowe okno, którego szerokość i wysokość wynoszą 7 cali. Wywołanie windows(width=7, height=5), windows(width=5, height=4), windows(width=3, height=2.5) spowoduje otwarcie trzech nowych okien różnej wielkości.
Chcąc mieć wykres zajmujący całą szerokość strony formatu A4 między marginesami wynoszącymi 2.5 cm musimy wykonać wykres o szerokości 16 cm. Odpowiadająca mu wysokość (tak by zajmował połowę strony) to 12 cm. Jeżeli przewidujemy podpis pod wykresem zazwyczaj skracamy jego wysokość do 9-10 cm. Należy wtedy rozpocząć robienie wykresu od polecenia:
w=16/2.54
h=10/2.54
windows(width=w, height=h)
|
lub krócej:
w=16/2.54
h=10/2.54
windows(w, h)
|
Przy braku nazw opcji trzeba pamiętać, że pierwsza liczba określać będzie szerokość wykresu, a druga jego wysokość. Podane wymiary odpowiadają typowemu rozmiarowi wykresu umieszczanego w pracach dyplomowych (wyjątkiem są złożone wykresy zajmujące całą stronę). Jest to standardowy rozmiar, gdy przyjmie się zasadę umieszczania wykresów w wykazie na końcu pracy. Gdy jednak ktoś zdecyduje się umieszczać wykresy w obrębie tekstu w miejscu ich cytowania, powinien zdecydować się na wymiary dwa razy mniejsze, tak by nie przeszkadzały one w czytaniu pracy. Gdy posyłamy pracę z wykresami do wydawnictwa, by została ona wydrukowana, należy przeczytać uwagi dla autorów umieszczane na stronach wydawnictwa. Są tam podane preferowane przez wydawnictwo wymiary wykresów (należy zwrócić przy tym uwagę w jakich jednostkach). Najlepiej ściśle się do nich dostosować.
Podział okna graficznego
Podział okna graficznego na nc kolumn o jednakowej szerokości i nr wierszy jednakowej wysokości może być zrealizowany za pomocą opcji mfcol=c(nr,nc) albo mfrow=c(nr,nc) funkcji par(). Funkcja par() pojawia się najczęściej po funkcji windows() i służy do organizacji okien graficznch (marginesów, wyglądów osi, tła wykresu i wielu innych opcji). Po zastosowaniu podziału okna graficznego, trzeba zastosować nc*nr nadrzędnych funkcji graficznych, które będą się wpisywać do kolejnych części okna graficznego.
windows(7.5,5)
par(mfcol=c(2,3))
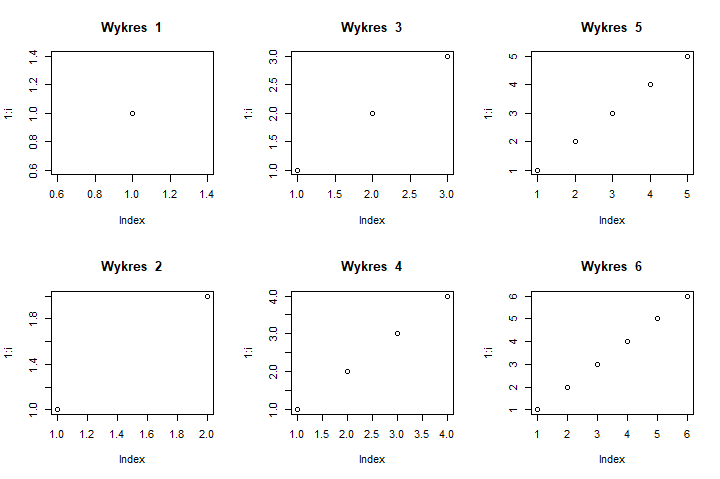
for (i in 1:6) plot(1:i, main=paste("Wykres ",i))
|
Po wykonaniu tego programu powstanie następujący wykres:
Porządkowanie kolejnych okienek okna graficznego jest tu wykonywane zgodnie z domyślnymi regułami porządkowania wyrazów w macierzach (od góry do dołu, a kolumny wykresów – od lewej do prawej). Ponadto zastosowanie opcji mfcol lub mfrow powoduje zmniejszenie wielkości czcionki i wielkości innych elementów graficznych (przy podziale na dwa jest to równoważne pomnożeniu pierwotnych wymiarów czcionki przez 0.83, a przy podziale na więcej części – pomnożeniu tych wymiarów przez 0.66).
Podział aktywnego okna graficznego na równe części można wykonać także za pomocą funkcji split.screen(c(n1,n2)). Okno graficzne zostanie wtedy podzielone na n1 razy w pionie i n2 razy w poziomie. Powstaje w ten sposób n1n2 części okna graficznego, w które można wpisać jakiś wykres wykonany nadrzędną funkcją graficzną. Każda część ma swój numer, przy czyn część 1 znajduje się w lewym górnym rogu, a kolejne numery są przyporządkowane częściom zgodnie z kierunkiem pisania (od lewej do prawej i z góry w dół). Wpisanie wykresu do n-tej części musi poprzedzić funkcja screen(n).
windows(4.5,2.5)
split.screen(c(1,2))
screen(1)
barplot(c(4,1,5,3))
screen(2)
barplot(c(5,3,1))
#
windows(2.5,4.5)
split.screen(c(2,1))
screen(1)
barplot(c(4,1,5,3))
screen(2)
barplot(c(5,3,1))
|
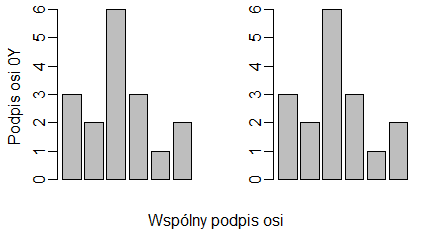
Powyższe programy spowodują wygenerowanie w aktywnym oknie dwóch następujących wykresów:
Funkcję split.screen() nie musi poprzedzać funkcja windows(). Potrafi ona sama wywołać okno graficzne o domyślnych wymiarach (7 cali wysokość i 7 cali szerokość). Ponadto ta sama funkcja może podzielić określoną część na n3n4 odpowiednio mniejszych części, co daje czasem pożądane efekty. Wykonuje to opcja screen=n. Po takim podziale te małe części uzyskują kolejne numery od n1n2+1 począwszy.
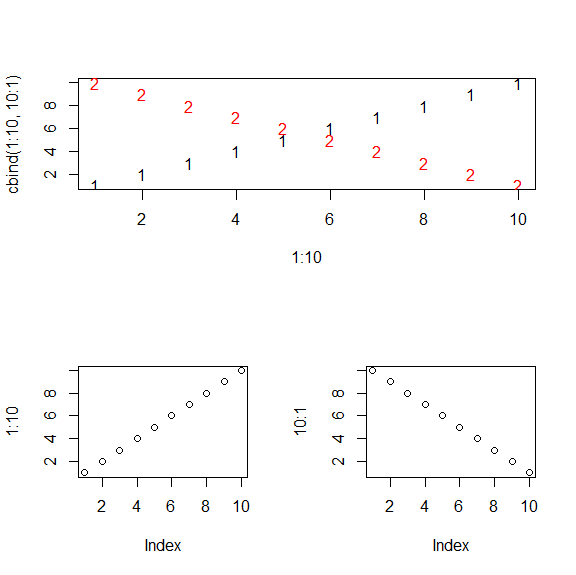
split.screen(c(2, 1))
split.screen(c(1, 2), screen=2)
screen(1)
matplot(1:10,cbind(1:10,10:1))
screen(3)
plot(1:10)
screen(4)
plot(10:1)
|
Program ten utworzy wykres postaci:
Większe możliwości dzielenia ekranu graficznego ma funkcja layout(matrix()). Związana z nią funkcja layout.show() pozwala na śledzenie tych zmian i zorientowanie się jakie numery są przyporządkowane poszczególnym częściom okna graficznego.
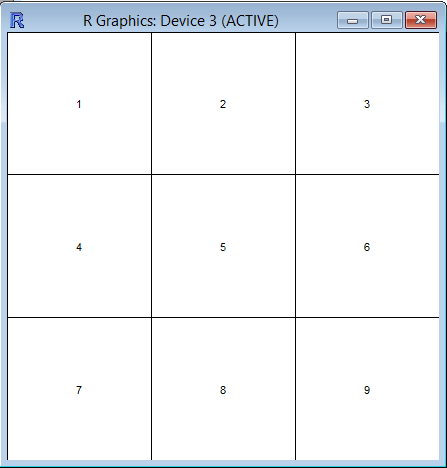
layout(matrix(1:9,3,3,byrow=TRUE))
layout.show(9)
|
Powyższe instrukcje spowodują, że okno graficzne wyglądać będzie następująco:
Przy wczytywaniu wykresów zarówno granice podziałów jak i numery znikną. Wczytanie wykresu w części n-tej spowoduje automatyczne przejście do części n+1-szej, gdy w programie pojawi się kolejna nadrzędna funkcja graficzna.
Poszczególne części okna graficznego wydzielonego przez funkcję layout() mogą dostać te same numery (wpisywane są one do macierzy). Wtedy wykres o tym numerze (zgodnie z kolejnością pojawiania się nadrzędnych funkcji graficznych) będzie znajdywał się w prostokącie obejmującym te części. Może to dawać efekty częściowego nakładania się na siebie wykresów.
windows(6,6)
layout(matrix(c(1,3,3,3,2,2,2,3,2,2,2,3,2,2,2,4),4,4))
layout.show(4)
plot(1:10)
plot(10:1)
plot(1:10)
plot(10:1)
|
Spowoduje to powstanie wykresu postaci:
Dodatkowo, funkcja layout() ma opcje wights=c() i heights=c(), za pomocą których można określić względne długości i szerokości poszczególnych części.
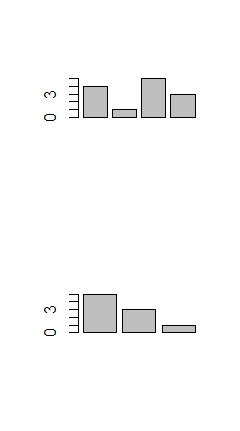
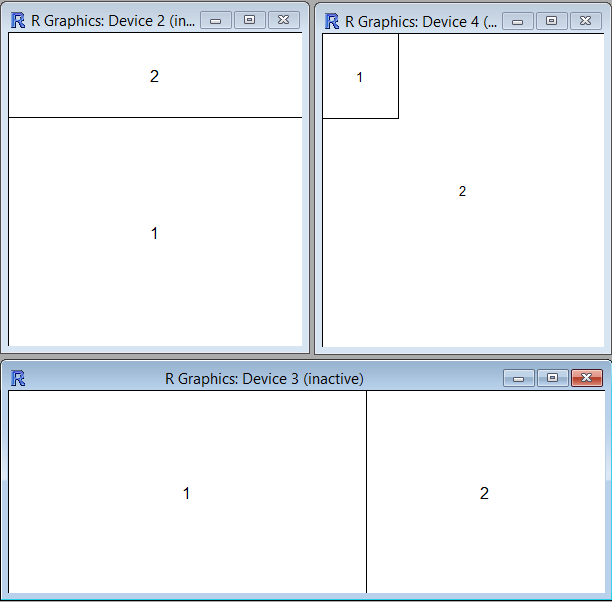
windows(2,2)
layout(matrix(2:1,2,1),heights=c(3,8))
layout.show(2)
windows(4.2,2)
layout(matrix(2:1,1,2),widths=c(3,2))
layout.show(2)
windows(2,2)
layout(matrix(c(1,2,2,2),2,2),widths=c(3,8),heights=c(3,8))
layout.show(2)
|
Spowoduje to następujące podziały trzech okienek graficznych (2,3 i 4).
Marginesy
Marginesy pojedynczych wykresów
Każdy wykres tworzony przez nadrzędne funkcje graficzne ma marginesy, na których umieszcza się etykiety osi, podpisy osi, tytuły lub podpisy wykresu, a często także legendę. Numeracja marginesów w R wygląda następująco:
- Margines dolny ma nr 1
- Margines lewy ma nr 2
- Margines górny ma nr 3
- Margines prawy ma nr 4
Po ustaleniu wymiarów okna graficznego, w pierwszej kolejności określa się wielkość marginesów wykresu. Margines liczony jest od granicy pola kreślenia do brzegów pola graficznego. Domyślne wielkości marginesów to:
- Margines dolny 1 cal = 2.54 cm
- Margines lewy 0.8 cala = 2.03 cm
- Margines górny 0.8 cala = 2.03 cm
- Margines prawy 0.4 cala = 1.01 cm
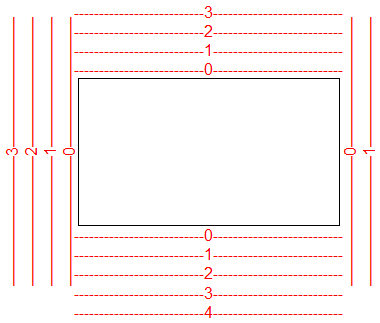
Marginesy dzielą się na linijki o szerokości 0.2 cala liczone od brzegu pola kreślenia do brzegu okna graficznego. Domyślnie:
- Margines dolny ma 5 linijek
- Margines lewy ma 4 linijki
- Margines górny ma 4 linijki
- Margines prawy ma 2 linijki
Na poniższym wykresie pokazane są na czerwono numery linijek, na jakie podzielono domyślne marginesy.
Domyślne wielkości marginesów ustalają się zawsze, gdy przed wywołaniem nadrzędnej funkcji graficznej nie pojawi się funkcja par() z opcją określającą wielkość marginesów. Przy małych wykresach domyślne marginesy mają nienormalnie duże wymiary, co było widać na wykresach w rozdziale 1, gdzie wielkość wykresów zmniejszono myszką. Czasami przy próbie utworzenia wykresu powstawał komunikat “figure margins too large”. Dlatego też w wszystkich programach graficznych standardem jest określanie wielkości marginesów po określeniu rozmiarów okna graficznego, a przed wywołaniem funkcji graficznej rysującej. Do konkretnych marginesów odnosimy się za pomocą ich numerów: liczb 1,2,3 i 4.
Funkcja par() służy do określenia wartości wszelkich opcji graficznych. Opcji tych ma 72, przy czym wiele z nich mają także funkcje graficzne nadrzędne i podrzędne, lecz nie wszystkie. Dotyczy to w szczególności wielkości marginesów. Zasada jest taka, że wartości opcji funkcji napisanych wcześniej są zmieniane przez wartości tych samych opcji napisanych później. Wielkość marginesów można określić za pomocą jednej z dwóch opcji:
- mai = c(x1, x2, x3, x4) gdzie x1, x2, x3, x4 są wielkościami marginesów dolnego, lewego, górnego i prawego w calach.
- mar = c(y1, y2, y3, y4) gdzie y1, y2, y3, y4 są wielkościami marginesów dolnego, lewego, górnego i prawego w “linijkach”
Wygląda to następująco:
windows(4.5, 2.5)
par(mai=c(0.5,0.5,0.1,0.1))
plot(1:10)
#
windows(4.5, 2.5)
par(mar=c(2,2,0.5,0.5))
plot(10:1)
|
Program powoduje pojawienie się dwóch wykresów wyglądających następująco:
Standardowy rozmiar wykresów do pracy dyplomowej (16×10 cm) z jednolinijkowymi podpisami osi wymaga najczęściej 4 linijki na margines dolny i 4 linijki na margines lewy. Domyślnie bowiem w czwartej linijce pojawiają się podpisy osi uzyskane za pomocą opcji xlab=”” i ylab=””. Jego zrobienie zaczyna się od podanych instrukcji:
w=16/2.54
h=10/2.54
windows(w, h)
par(mar=c(4,4,0,0))
plot(1:10, xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
|
Program ten wygeneruje następujący wykres:
Warto przy tym pamiętać, że umiejscowienie etykiet jak i podpisów można zmienić za pomocą opcji funkcji par(), o czym będzie mowa w rozdziale o podpisach i napisach.
Czasami zamiast zmieniać szerokość marginesu lepiej zmienić obszar kreślenia. Służy do tego opcja pin=c(x,y) funkcji par(), gdzie x i y są szerokością i wysokością wykresu wyrażoną w calach. Umieszcza ona obszar kreślenia w środku okna graficznego i nie zmienia go przy zmianach wielkości tego okna.
windows(4.5, 2.5)
par(pin=c(4,2))
plot(1:10)
#
windows(4.5, 2.5)
par(pin=c(3,1))
plot(1:10)
|
Program ten spowoduje powstanie dwóch wykresów:
Marginesy złożonych rycin
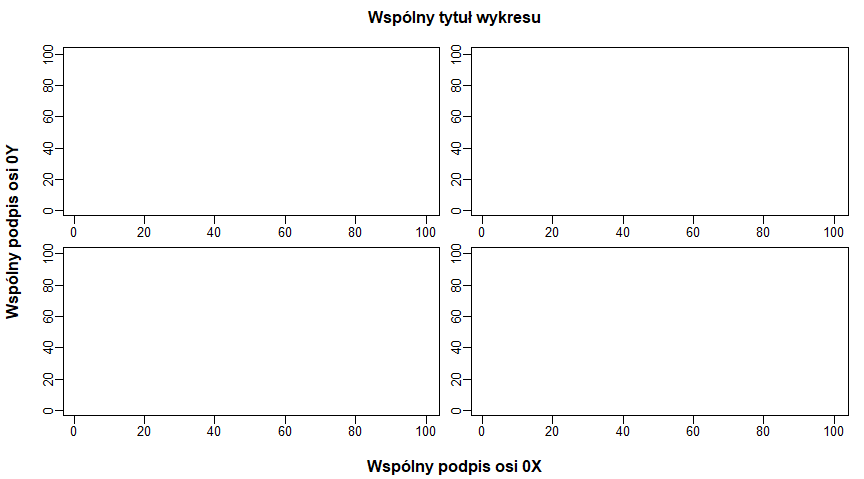
W poprzednim rozdziale pokazano jak podzielić okno graficzne, aby na jednej rycinie umieścić kilka wykresów. Dość często trzeba pod taką grupą wykresów umieścić jeden komentarz albo wspólny podpis dwóch lub więcej osi. Potrzebne są na to marginesy obejmujące całe pole graficzne, gdyż domyślnie mają one grubość 0, podczas gdy w każdej wydzielonej części pola graficznego mają grubość określoną opcją mai=c(x1, x2, x3, x4) lub mar=c(y1, y2, y3, y4). Opcje funkcji par(), które pozwalają na utworzenie takich wspólnych marginesów noszą nazwy:
- omi = c(x1, x2, x3, x4) gdzie x1, x2, x3, x4 są wielkościami wspólnych marginesów dolnego, lewego, górnego i prawego w calach.
- oma = c(y1, y2, y3, y4) gdzie y1, y2, y3, y4 są wielkościami wspólnych marginesów dolnego, lewego, górnego i prawego w “linijkach”
Zastosowanie jednej z tych opcji przed funkcją split.screen() lub layout() spowoduje, że najpierw zostanie określony margines wspólny i podziałowi ulegnie tylko pozostała (środkowa) część pola graficznego. Wygląda to następująco:
windows(4.5, 4.5)
par(mar=c(1,1,0,0))
layout(matrix(1:9,3,3,byrow=TRUE))
layout.show(9)
#
windows(4.5, 4.5)
par(mar=c(1,1,0,0),oma=c(4,4,0,0))
layout(matrix(1:9,3,3,byrow=TRUE))
layout.show(9)
|
Podziały okna graficznego ujawnione funkcję layout.show() będą wyglądały następująco:
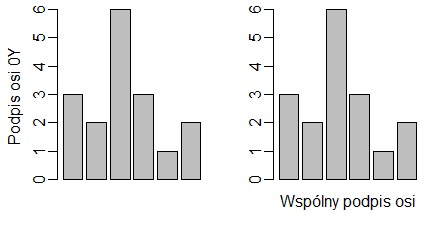
W funkcji par() istnieje także opcja mfrow=c(n1,n2) podziału okna graficznego na tyle równych części ile wykazuje liczba n1*n2 umieszczonych w n1 rzędach i n2 kolumnach. Opcja oma=c(x1,x2,x3,x4) umieszcza margines wokół tego zestawu wykresów.
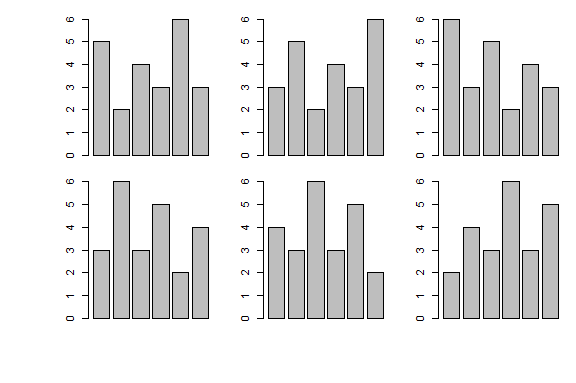
windows(6,4)
par(mar=c(1,3,1,1),oma=c(4,4,0.5,0),mfrow=c(2,3))
barplot(c(5,2,4,3,6,3))
barplot(c(3,5,2,4,3,6))
barplot(c(6,3,5,2,4,3))
barplot(c(3,6,3,5,2,4))
barplot(c(4,3,6,3,5,2))
barplot(c(2,4,3,6,3,5))
|
Uzyskany wykres wygląda następująco:
Pole kreślenia
Wymiary pola kreślenia
Pole kreślenia zawsze jest prostokątem. Jego wymiary można wyliczyć w calach jako:
długość = długość pola graficznego – szerokość marginesu prawego – szerokość marginesu lewegowysokość = wysokość pola graficznego – szerokość marginesu dolnego – szerokość marginesu górnegoNie ułatwia to jednak nawigacji w jego obrębie. Bowiem każdy punkt pola kreślenia ma współrzędne wynikające z danych, z których utworzony został wykres. Przykładowo polecenie plot(1:10) tworzy pole kreślenia, którego dolny lewy róg ma współrzędne (0.64, 0.64) a prawy górny róg ma współrzędne (10.36, 10.36). Są to współrzędne odczytane z automatycznie tworzonego w polu kreślenia fragmentu kartezjańskiego układu współrzędnych, takiego samego jakiego uczą na lekcjach matematyki. Jest on tak tworzony, aby obejmował z nawiązką wszystkie dane, które mają pojawić się w polu kreślenia. W pokazanym przykładzie prostokąt o lewym dolnym rogu (0.64, 0.64), a prawym górnym (10.36, 10.36) obejmuje z nawiązką wszystkie punkty wykreślone jako 1:10 × 1:10.
Granice pola kreślenia wyliczymy za pomocą funkcji par() obliczając jej wartość dla zmiennej tekstowej “usr”. Wygląda to następująco:
> plot(1:7)
> par("usr")
[1] 0.76 7.24 0.76 7.24
> pie(1:7)
> par("usr")
[1] -1.20802 1.20802 -1.08000 1.08000
> windows(4.5, 2.5)
> pie(1:7)
> par("usr")
[1] -5.42009 5.42009 -1.08000 1.08000
> barplot(1:7)
> par("usr")
[1] -0.128 8.728 -0.070 7.000
> boxplot(1:7)
> par("usr")
[1] 0.46 1.54 0.76 7.24
|
Za wyjątkiem funkcji pie() wielkości te nie ulegają zmianie przy zmianach wielkości pola graficznego spowodowanego manipulacjami myszką lub ustaleniami w funkcji windows(). Funkcja pie() ma wbudowane instrukcje powodujące, że w każdym kształcie pola kreślenia jest kołem o środku w punkcie (0,0), a to powoduje zmiany pola kreślenia przy zmianach stosunku jego długości do wysokości.
Inne dane wygenerują przy tych samych funkcjach graficznych inne współrzędne granic pola kreślenia. Są one bowiem tak określone, aby wartości liczbowe danych umieszczane na wykresie mieściły się między tymi granicami. Domyślnie przyjęta została zasada:
- Wykres umieszczony jest w domyślnym kartezjańskim układzie współrzędnych.
- Wyliczana jest minimalna xmin i maksymalna xmax wartość na osi 0X, tak by cały wykres mieścił się na odcinku [xmin, xmax].
- Jeżeli w opcjach wykresu określona jest opcja xlim=c(x1,x2) to xmin=x1 i xmax=x2.
- Wyliczany jest minimalna ymin i maksymalna ymax wartość na osi 0Y, tak by cały wykres mieścił się miedzy ymin a ymax.
- Jeżeli w opcjach wykresu określona jest opcja ylim=c(y1,y2) to ymin=y1 i ymax=y2.
- Od wartości minimalnej xmin odejmowanych jest 4% długości odcinka [xmin, xmax], a do wartości maksymalnej dodawana jest wartość równa 4% długości tego odcinka
- Od wartości minimalnej ymin odejmowanych jest, a do wartości ymax dodawana jest wartość równa 4% długości odcinka [ymin, ymax].
- Uzyskane liczby są przeskalowywane na obszar wykresu między wyznaczonymi marginesami i wykres jest rysowany.
Efektem tego jest możliwość posługiwania się układem współrzędnych pola kreślenia w celu dokonania zmian lub dorysowywania czegoś na wykresie.
Oznaczanie granic pola kreślenia
Poszczególne funkcje graficzne domyślnie albo generują, albo nie generuję granice pola kreślenia. Umieszczają lub nie osie na tych granicach (zwłaszcza dolną i lewą). Można tym sterować za pomocą następujących opcji funkcji graficznych sterujących:
- axes=TRUE Gdy osie mają się pojawić na wykresie (nie działa w funkcji pie()).
- frame=TRUE Gdy obramowanie ma być na wykresie (nie działa dla funkcji pie() i barplot()).
- ann=TRUE Gdy domyślne tytuły osi mają być na wykresie (nie działa dla funkcji pie() i barplot()).
Działają one w następujący sposób:
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(10:0, frame=FALSE, ann=FALSE)
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
boxplot(10:0, frame=FALSE, ann=FALSE)
|
Programy te spowodowały, że na wykresach pozostały tylko osie. Są one wykreślane tylko od wartości najmniejszej etykiety do największej.
Ponieważ opcja frame=TRUE nie działa w niektórych funkcjach graficznych wydaje się, że wykreślenie granic pola kreślenia na wykresie nie jest dla nich możliwe. Nie jest tak źle. Istnieje bowiem podrzędna funkcja graficzna box(), która zakreśla pole kreślenia i w dodatku ma opcje, które pozwalają wybrać styl i kolor linii zakreślającej to pole.
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(10:0, frame=FALSE, ann=FALSE, axes=FALSE)
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
pie(10:0, ann=FALSE)
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
barplot(10:0, ann=FALSE, axes=FALSE)
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
boxplot(10:0, frame=FALSE, ann=FALSE, axes=FALSE)
box()
|
Programy te wygenerowały cztery wykresy:
We wszystkich wykresach zostało najpierw usunięte całe obramowanie i osie (o ile istniało), a następnie narysowane granice pola kreślenia.
Nawigacja w obrębie pola kreślenia
Znajomość współrzędnych granic pola kreślenia pozwala na umiejscowienie różnych elementów na polu kreślenia, gdyż współrzędne miejsca gdzie ma być coś dorysowane lub dopisane są obowiązkowym argumentem niemal wszystkich podrzędnych funkcji graficznych. Muszą one wskazywać punkty znajdujące się w polu kreślenia, gdyż kiedy wskażą punkt poza tym polem nic się nie dorysuje.
Przy funkcjach plot(), matplot() oraz curve() boxplot() oraz hist() wskaźnikiem pozwalającym na odczytanie współrzędnych punktów mieszczących się w polu kreślenia są liczby umieszczane na osiach. Nie trzeba wtedy wywoływać funkcji par(“usr”). Można to zobaczyć na przykładzie podrzędnej funkcji graficznej points() dorysowującej punkty do wykresu, której obowiązkowymi argumentami są wektor pierwszych i wektor drugich współrzędnych wykreślanych punktów.
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(1:7, 7:1+3)
points(1:5, 5:1+3)
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
curve(sin, -pi, pi)
points(c(-pi,pi), c(1,-1))
|
Po uruchomieniu tego programu powstają dwa wykresy:
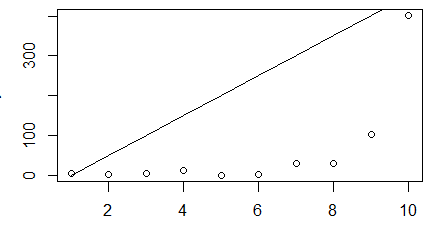
Opisana zasada działa także w przypadku wykresów o zlogarytmowanych jednej lub obu osiach. Pokazano to przy zastosowaniu podrzędnej funkcji graficznej lines() dokładającą łamaną do wykresu, w której obowiązkowymi argumentami są której obowiązkowymi argumentami są wektor pierwszych i wektor drugich współrzędnych punktów połączonych odcinkami.
y = c(4.84, 1.12, 3.57, 10.57, 0.12, 2.55, 30.10, 30.18, 100.93, 400.15)
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(1:10, y)
lines(1:10,0:9*50+0.1)
#
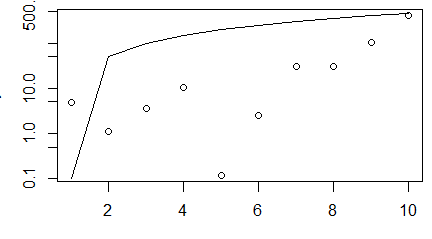
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(1:10, y, log="y")
lines(1:10,0:9*50+0.1)
|
Programy te różnią się wyłącznie tym, że jedna z osi drugiego wykresu jest logarytmiczna. Łamana będąca prostą na pierwszym wykresie zmienia się na łamaną na drugim.
Pewne problemy może sprawiać funkcja barplot(), gdyż nie tworzy ona osi poziomej wskazującej współrzędne punktów w polu kreślenia. Dopiero po dłuższym szukaniu można znaleźć przyjęte zasady tworzenia słupków: lewy brzeg pierwszego słupka jest na linii x=0, słupkom przyporządkowano domyślną szerokość 1, a odstępy między nimi wynoszą 0.2. Okazuje się, jednak, że funkcja ta obok zrobienia wykresu tworzy także jednokolumnową macierz liczb będącymi współrzędnymi środków słupków. Można je wykorzystać do modyfikacji wykresu.
windows(4.5, 2.5)
par(mar=c(0.5, 3, 0.5, 0.5))
barplot(1:7)
points(1:7, 1:7-0.5)
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 0.5, 0.5))
a=barplot(1:7)
points(a, 1:7-0.5))
|
Programy te utworzyły dwa wykresy:
Tylko w drugim dołożone punkty wypadły w środku słupków. W pokazanym przykładzie macierz środków słupków wygląda następująco:
> a=barplot(1:7)
> a
[,1]
[1,] 0.7
[2,] 1.9
[3,] 3.1
[4,] 4.3
[5,] 5.5
[6,] 6.7
[7,] 7.9
|
Gdy argumentem tej funkcji barplot() jest macierz kilkukolumnowa zasada rozmieszczania słupków już już inna:
> a=barplot(cbind(1:3, 3:1, c(1,3,2)), beside=TRUE)
> a
[,1] [,2] [,3]
[1,] 1.5 5.5 9.5
[2,] 2.5 6.5 10.5
[3,] 3.5 7.5 11.5
|
Jednocześnie powstał następujący wykres:
Warto zapamiętać o pokazanej właściwości funkcji barplot(), gdyż bardzo ułatwia modyfikowanie wykresów przez nią utworzonych.
Modyfikacja pola kreślenia
Rozmiary i przydzielenie skali liczbowej polu kreślenia przebiegają w kilku etapach obejmuje etap odjęcie od wartości minimalnych wykresu wielkości odpowiadającej 4% długości oraz wysokości wykresu i dodanie do wartości maksymalnych wielkości odpowiadającej 4% długości i wysokości wykresu. Etap ten powoduje, że żaden z elementów wykresu nie znajdzie się na osi lub na brzegu pola kreślenia, gdzie może być tylko połowicznie narysowany. Jednocześnie może powodować nieco mylną interpretację niektórych wykresów, gdyż przywykliśmy, że osie wykresów przecinają się w punkcie (0,0). W niektórych sytuacjach lepiej jest zlikwidować etap drugi, przynajmniej w stosunku do jednej osi. Wykonuje się to opcjami xaxs i yaxs funkcji par() domyślnie przyjmującymi wartości “r” (ustawienie standardowe). Należy im nadać wartość “i”.
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(0:10)
par("usr")
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xaxs="i")
plot(0:10)
par("usr")
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), yaxs="i")
plot(0:10)
par("usr")
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xaxs="i", yaxs="i")
plot(0:10)
par("usr")
|
Program tworzy 4 wykresy:
Jednocześnie zmieniają się współrzędne dolnego lewego i górnego prawego rogu pola kreślenia, co wykrywamy funkcją par(“usr”):
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5))
> plot(0:10)
> par("usr")
[1] 0.6 11.4 -0.4 10.4
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5), xaxs="i")
> plot(0:10)
> par("usr")
[1] 1.0 11.0 -0.4 10.4
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5), yaxs="i")
> plot(0:10)
> par("usr")
[1] 0.6 11.4 0.0 10.0
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5), xaxs="i", yaxs="i")
> plot(0:10)
> par("usr")
[1] 1 11 0 10
>
|
Dodam, że funkcja plot() dla pojedynczego wektora tworzy rozrzut punktów (i, x[i]) gdzie i jest liczone od 1. Zatem minimalna wartością na osi 0X jest 1 a maksymalna 11. Na osi 0Y minimalną wartością jest 0 a maksymalną 10.
Czasami potrzebne są sztuczne zmiany zakresu wykreślania danych. Rządzą tym opcje nadrzędnych funkcji graficznych:
- xlim=c(x1,x2) Minimalna wartość na osi 0X równa x1 i maksymalna równa x2.
- ylim=c(y1,y2) Minimalna wartość na osi 0Y równa y1 i maksymalna równa y2.
Opcje te zmieniają etap pierwszy wyznaczania pola kreślenia, nie wpływając na etap drugi.
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(0:10, xlim=c(0,5), ylim=c(0,10))
par("usr")
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
plot(0:10, xlim=c(0.34,5.72), ylim=c(-0.11,10.53))
par("usr")
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
barplot(0:10, xlim=c(0,5), ylim=c(2,10))
par("usr")
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5))
boxplot(0:10, -1:11, xlim=c(0,5), ylim=c(2,10))
par("usr")
|
Cztery wykresy tworzone przez ten program wyglądają następująco:
Ograniczenie zakresu rysowania na osi pionowej spowodowały przesunięcie obrazu funkcji barplot() oraz boxplot() na margines dolny i obcięcie części wykresu. Z tym, że dla funkcji barplot() częsci znajdujace się na marginesach zostały ujawnione a dla funkcji boxplot() nie. Dzieje się to dlatego, że jedną z opcji funkcji barplot() jest xpd mająca domyślnie wartość TRUE. Opcja logiczna xpd stosowana jest najczęscie w funkcji par() i domyślnie przyjmuje wartość FALSE co nie pozwala niczego dorysowywać lub dopisywać na marginesach. Dopiero zastosowanie par(xpd=TRUE) pozwala na takie operacje. Jednak taka sama opcja w funkcji nadrzędnej może to zmienić, choć dotyczy to tylko wykonania funkcji nadrzędnej. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xpd=FALSE)
barplot(0:10, xlim=c(0,5), ylim=c(2,10), xpd=TRUE)
par("usr")
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xpd=TRUE)
barplot(0:10, xlim=c(0,5), ylim=c(2,10), xpd=FALSE)
par("usr")
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xpd=FALSE)
boxplot(0:10,-1:11, xlim=c(0,5), ylim=c(2,10), xpd=FALSE)
par("usr")
box()
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), xpd=TRUE)
boxplot(0:10,-1:11, xlim=c(0,5), ylim=c(2,10), xpd=FALSE)
par("usr")
box()
|
Powstałe wykresy wyglądają następująco:
Funkcja boxplot() nie ma wogóle opcji xpd i reaguje wyłącznie na wartość tej opcji w funkcji par().
Współrzędne rogów pola kreślenia, ujawnione w konsoli przy okazji wykonywania ostatniego programu, wyglądają następująco:
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5))
> plot(0:10, xlim=c(0,5), ylim=c(0,10))
> par("usr")
[1] -0.2 5.2 -0.4 10.4
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5))
> plot(0:10, xlim=c(0.34,5.72), ylim=c(-0.11,10.53))
> par("usr")
[1] 0.1248 5.9352 -0.5356 10.9556
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5))
> barplot(0:10, xlim=c(0,5), ylim=c(2,10))
> par("usr")
[1] -0.2 5.2 2.0 10.0
> box()
>
> windows(4.5, 2.5)
> par(mar=c(3, 3, 0.5, 0.5))
> boxplot(0:10, xlim=c(0,5), ylim=c(2,10))
> par("usr")
[1] -0.20 5.20 1.68 10.32
|
Zmiana pola kreślenia i tworzenie wykresów o osi dodatkowej
Czasami już po utworzeniu wykresu trzeba zmienić współrzędne pola kreślenia gdy chcemy na nim dorysować dane wyliczane w innych jednostkach i mające inne wartości. Innymi słowy, gdy chcemy zastosować wykres z dwoma osiami 0Y. W tym wypadku musimy sami przyjrzeć się dokładanym danym, znaleźć ich wartość minimalną i maksymalną na osi 0X i 0Y i posłużyć się funkcją plot.window(). Jej obowiązkowymi argumentami są xlim=c(xmin,xmax) oraz ylim=c(ymin,ymax). Funkcja działa tylko, gdy już został utworzony jakiś wykres z określonym polem kreślenia. Służy zatem tylko do zmiany jego układu współrzędnych przy czym sama dokłada z każdej strony 4% długości i wysokości wynikających z podanych granic w opcjach xlim i ylim (o ile opcje xaxs i yaxs nie decydują inaczej).
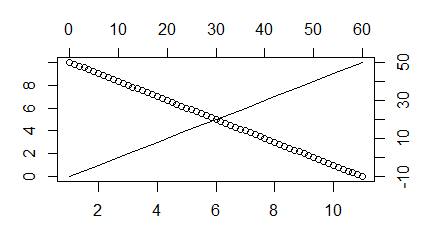
windows(4.5, 2.5)
par(mar=c(3, 3, 3, 3))
plot(0:10, type="l")
plot.window(c(0,60),c(-10,50))
points(0:60, 50:-10)
axis(3)
axis(4)
|
Program generuje następujący wykres:
Osie
Elementy tworzące osie
Na wykresach umieszcza się zazwyczaj dwie osie na dole pola kreślenia i na lewym boku pola kreślenia. Bywa jednak, że na jednym wykresie umieszcza zmienne wyliczane w nieporównywalnych ze sobą jednostkach i wartości jednej z tych zmiennych umieszcza się na osi z prawej strony wykresu. To samo dotyczyć może osi 0X, które dla różnych krzywych mogły być wyliczane innym sposobem. Ogólnie zatem można wyróżnić cztery osie. Mają one numery ułożone podobnie jak marginesy.
- 1 – Numer osi dolnej.
- 2 – Numer osi lewej.
- 3 – Numer osi górnej.
- 4 – Numer osi prawej.
Można to zobaczyć stosując dla standardowego wykresy najpierw opcje axes=FALSE, co powoduje, że domyślne osie nie pojawią się a następnie stosując funkcje axis(), której obowiązkowym argumentem jest numer osi.
windows(4.5, 2.5)
par(mar=c(3,3,2,2))
plot(1:7, axes=FALSE)
axis(1)
#
windows(4.5, 2.5)
par(mar=c(3,3,2,2))
plot(1:7, axes=FALSE)
axis(2)
#
windows(4.5, 2.5)
par(mar=c(3,3,2,2))
plot(1:7, axes=FALSE)
axis(3)
#
windows(4.5, 2.5)
par(mar=c(3,3,2,2))
plot(1:7, axes=FALSE)
axis(4)
|
Program generuje 4 wykresy z jedną narysowaną osią.
Opcja axes=FALSE likwiduje wszystkie osie domyślne wykresu wraz z ich etykietami. Gdy chcemy modyfikować tylko oś 0X, a oś 0Y pozostawić domyślną, wystarczy w nadrzędnej funkcji graficznej lub poprzedzającej ją funkcji par() zastosować opcję xaxt=”n”, natomiast gdy chcemy modyfikować oś 0Y pozostawiając domyślną oś 0X wystarczy napisać yaxt=”n”. Te opcje pozostawiają obramowanie wykresu, o ile istnieje.
Każda oś składa się z odcinka leżącego na granicy pola kreślenia, znaczników, etykiet i podpisu. Ich umieszczenie, rozmieszczenie, orientację, wielkość, kolor, typem linii odcinka, wielkość i rodzaj czcionki etykiet i podpisów możemy zmienić za pomocą opcji funkcji par(), nadrzędnej funkcji graficznej jak i funkcji axis(). Dość często są to jedne i te same opcje. O kolorach, wzorach, wielkości i krojach czcionki będzie mowa w odpowiednich rozdziałach. Oto wykaz najczęściej opcji służących do modyfikacji umieszczenia osi, rozmieszczenia jej elementów, orientacji etykiet oraz podpisów pod osiami.
- mgp=c(z,y,x) Rozmieszczenie osi (x), etykiet (y) i podpisów (z) na wykresie i względem siebie.
- at = c() Wykaz miejsc, gdzie mają zostać umieszczone znaczniki,
- labels = c() Wykaz nazw, które mają pojawić się pod znacznikami, labels = NA – brak nazw,
- tick=FALSE Opcja mówiąca, że w ogóle nie ma być znaczników,
- line=n Umiejscowienie osi w stosunku do miejsca domyślnego (n=0). Liczone jest liczbą linijek, w jakich mieści się tekst równoległy do osi. Może mieć wartości dodatnie (wchodzi na marginesy) lub ujemne – wchodzi w obszar kreślenia),
- tck = x Długość znaczników i ich kierunek (x dodatnie – znaczniki wewnątrz pola kreślenia, ujemne – na zewnątrz,
- lwd.ticks=n Grubość linii znaczników,
- hadj = 0, hadj = 0.5, hadj = 1 Wyrównanie etykiet pod znacznikami: do lewej, do środka i do prawej,
- padj = 0, padj = 1 Umiejscowienie etykiet pod znacznikami: z prawej / na górze albo z lewej / na dole w zależności od numeru osi.
Umieszczenie osi na wykresie i rozmieszczenie elementów osi
Często podpisy osi albo wartości zmiennych umieszczonych na osiach, należałoby przybliżyć lub oddalić od osi. Czasami wygodnie jest by sama oś była w innym miejscu niż brzeg pola kreślenia. Najczęściej wykonuje się to opcją mgp=c(z,y,x), która może być opcja funkcji par(), nadrzędnej funkcji graficznej lub funkcji axis(). Gdy jest zawarta w funkcji par() dotyczy wszystkich wykresów, które się za nią pojawią i dotyczy wszystkich osi. Gdy jest w obrębie nadrzędnej funkcji graficznej, dotyczy tylko tego wykresu i dotyczy wszystkich jego osi, a gdy znajduje się w funkcji axis() dotyczy tylko tej osi, która jest podana w tej funkcji. Liczba x dotyczy miejsca gdzie jest rysowany odcinek osi. Liczona jest w “linijkach” czyli krotności odległości 0.2 cala od brzegu pola kreślenia. Domyślnie ma wartość 0. Dodatniej jej wartości powodują “zjechanie” osi na marginesy, ujemne “wjechanie” na pole kreślenia. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,0.2,0.2), mgp=c(0, -1, -2))
plot(1:7, frame=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
#
windows(4.5, 2.5)
par(mar=c(3,3,0.2,0.2))
plot(1:7, frame=FALSE, mgp=c(0, -1, -2), xlab="Podpis osi 0X",
ylab="Podpis osi 0Y")
#
windows(4.5, 2.5)
par(mar=c(3,3,0.2,0.2))
plot(1:7, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
axis(1, mgp=c(0,-1,-2) )
axis(2, mgp=c(2,1,0))
|
Program tworzy trzy wykresy:
Dwa z nich wyglądają tak samo. W trzecim inaczej rozmieszczone są osie 0X i 0Y, ale jednocześnie znikły podpisy pod osiami, które należy dopisać odpowiednimi podrzędnymi funkcjami graficznymi.
Najczęściej jednak przesuwa się każdą z oś osobno i służy do tego opcja line=n funkcji axis(). Nie zmienia ona rozmieszczenia względem siebie znaczników i etykiet ustalonych w funkcji par() za pomocą opcji mgp=c(z,y,x). Co więcej dodanie tej opcji do funkcji par() powoduje, że wyświetlają się podpisy pod osiami ustawionymi domyślnie.
windows(4.5, 2.5)
par(mar=c(3,3,0.2,0.2))
plot(1:7, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
axis(1)
axis(2)
axis(2, line=-11, at=1:7, labels=1:7*10)
#
windows(4.5, 2.5)
par(mar=c(3,3,0.2,0.2), mgp=c(1.3,0.5,0))
plot(1:7, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
axis(1)
axis(2)
axis(2, line=-11, at=1:7, labels=1:7*10)
|
Program generuje dwa wykresy:
Przedstawiony wykres z dwoma osiami 0Y dotyczy hipotetycznej sytuacji gdy wydzielona z prawej strony część danych ma tak duże wartości, że lepiej jest dla nich stosować inna jednostkę pomiaru.
Liczba, rozmieszczenie i wielkość znaczników
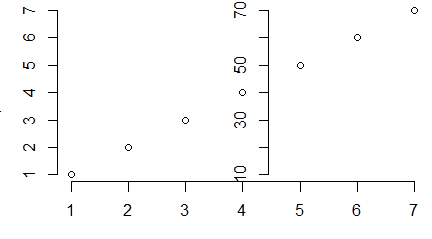
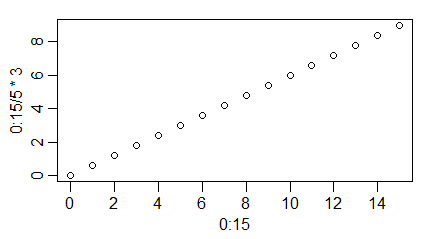
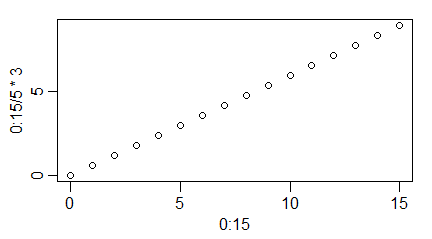
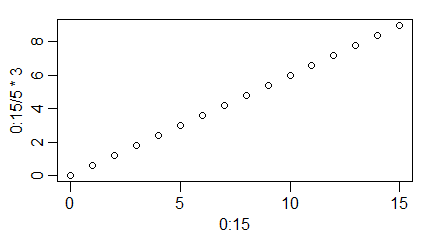
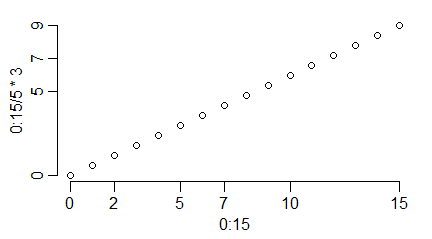
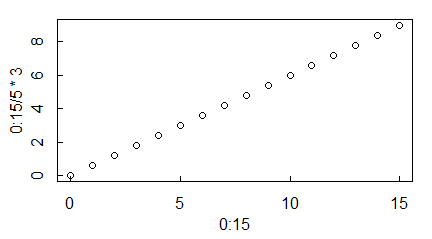
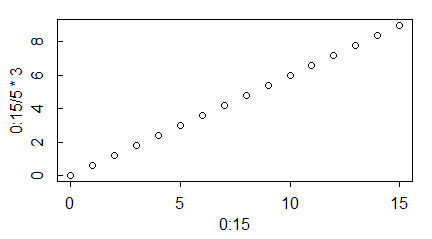
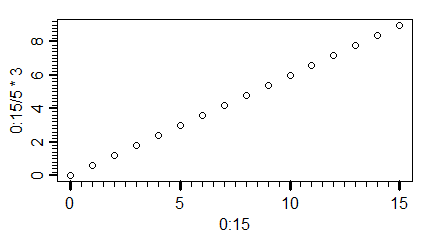
Funkcje graficzne proponują podział osi na jednostki stosują one różne algorytmy, które dzielą oś tak, aby znaczniki występowały dla zaokrąglonych wartości zmiennych i aby pokazywane wartości zmiennych obok osi nie zachodziły na siebie. Czasami jednak chcemy by znaczniki były umieszczane gęściej lub rzadziej w stosunku do tego, co zaproponował program. Modyfikuje to częściowo opcja lab=c(n1,n2,n3) funkcji par() lub nadrzędnej funkcji graficznej, gdzie n1 oznacza przybliżoną liczbę znaczników na osi 0X, do której algorytm ma się zastosować, n2 to samo dla osi 0Y, n3 – kreślą długość wektora etykiet (jest jednak przez R ignorowana).
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0), lab=c(6,6,1))
plot(0:15,0:15/5*3 )
#
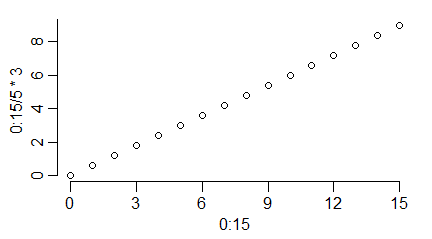
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0), lab=c(4,3,1))
plot(0:15,0:15/5*3)
#
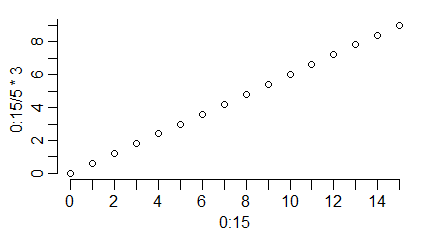
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0) )
plot(0:15,0:15/5*3, lab=c(4,6,1))
|
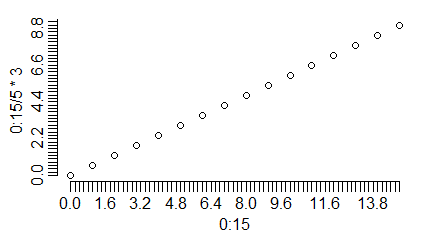
Program wykonuje następujące wykresy:
Znacznie częściej organizuje się znaczniki w funkcjach axis(), które dają pełną możliwość kontroli ich liczby. Robi to opcja at=c(), której wartościami są liczby pokazujące odpowiednią współrzędną punktu, w którym ma być znacznik (dla osi poziomych – pierwsze współrzędne, dla osi pionowych – drugie).
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,at=0:5*3)
axis(2,at=0:5*2)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,at=0:15)
axis(2,at=0:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,at=0:75/5)
axis(2,at=0:50/5)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,at=c(0,2,5,7,10,15))
axis(2,at=c(0,5,7,9))
|
Program ten rysuje następujące wykresy:
Etykiety są zawsze pod którymś znacznikiem, ale nie pod wszystkimi. Specjalny algorytm pomija te etykiety, które zachodzą na pole wykreślonej już etykiety.
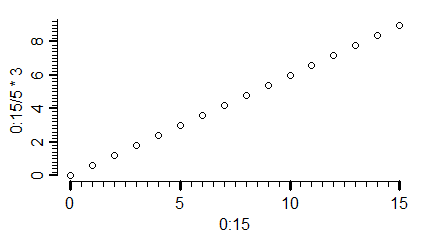
Długość znaczników można określić opcją tck=x, gdzie standardowo x=-0.05. Wartości dodatnie tej opcji pokazują długość znaczników wchodzących do środka pola kreślenia. Grubość znacznika można określić opcją lwd.tick=y.
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, tck=0.03)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,tck=-0.03)
axis(2,tck=0.03)
box()
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,tck=-0.05, lwd.ticks=3)
axis(1,tck=-0.03, at=0:30/2, labels=NA)
axis(2,tck=-0.05,lwd.ticks=2)
axis(2,tck=-0.03, at=0:50/5, labels=NA)
|
Wykresy rysowane przez ten program wyglądają następująco:
Opcje tck=x i lwd.ticks=y można zastosować w funkcji par() poprzedzającej wykres i już nie modyfikować jej dalej. Jest to wygodne, gdy przygotowuje się serię wykresów, których ogólny wygląd ma być taki sam.
R posiada specjalną funkcję graficzną podrzędną rug() rysujacą znaczniki na dowolnej osi zgodnie z wartościami zadanego wektora. Znaczniki te mogą, ale nie muszą mieć wtedy cokolwiek wspólnego z etykietami na osi, mogą pokazywać współrzędne punktów na wykresie:
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(0:15,0:15/5*3, axes=FALSE)
axis(1,tck=-0.05, lwd.ticks=3)
rug(0:30/2, -0.03, 1)
axis(2,tck=-0.05,lwd.ticks=2)
rug(0:50/5, -0.03, 2)
box()
#
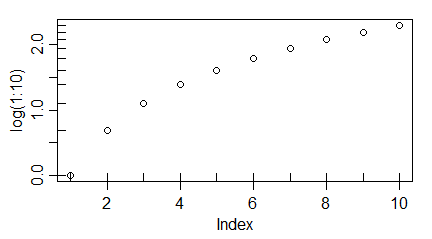
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.6,0))
plot(log(1:10), axes=FALSE)
axis(1, tck=-0.05)
rug(1:10, 0.05, 1)
axis(2, tck=-0.05)
rug(log(1:10), 0.05, 2)
box()
|
Pierwszy wykres w zasadzie jest powtórzeniem wykonanego wcześniej wykresu i pokazuje jak funkcja axis() z opcją labels=NA może zostać zastąpiona przez funkcje rug(). Drugi wykres pokazije mozliwość wprowadzania znaczników osi jako odczyt współrzędnych punktów obok typowych znaczników osi z etykietami.
Umiejscowienie i orientacja etykiet
Etykiety standardowo umiejscowione są pod lub obok znaczników i pisane są tylko wtedy, gdy jest dla nich miejsce. Czasami, aby wykresy miały etykiety o innych wartościach, niż proponuje to program, trzeba zwiększyć zasięg pola kreślenia opcją xlim=c(x1,x2) lub ylim=c(y1,y2) pisaną najczęściej w nadrzędnej funkcji rysującej. Znacznie lepiej jest jednak zrobić samemu osie z porządnymi etykietami za pomocą opcji at funkcji axis() lub zrobić jedno i drugie.
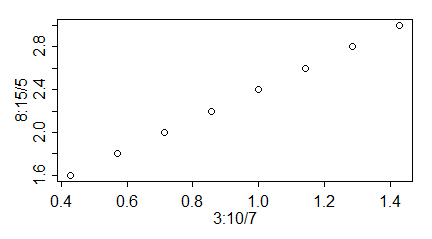
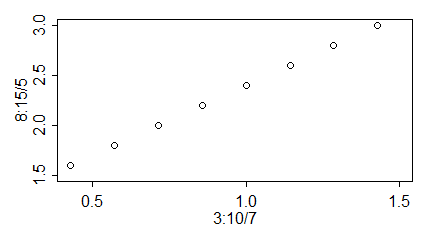
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.4,0.5,0), tck=-0.03)
plot(3:10/7, 8:15/5)
#
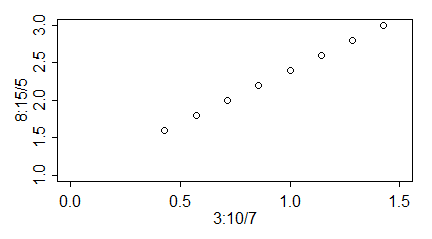
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.4,0.5,0), tck=-0.03)
plot(3:10/7, 8:15/5, xlim=c(0,1.5), ylim=c(1,3))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.4,0.5,0), tck=-0.03)
plot(3:10/7, 8:15/5, axes=FALSE, xlim=c(3/7,1.5), ylim=c(1.5,3))
axis(1,at=1:3/2)
axis(2,at=3:6/2)
box()
|
Program daje następujące wykresy:
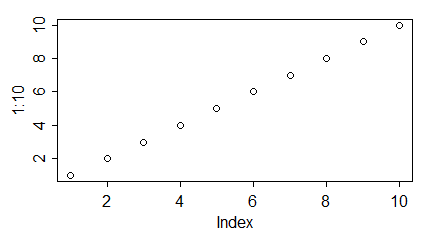
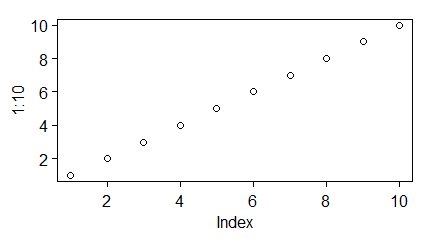
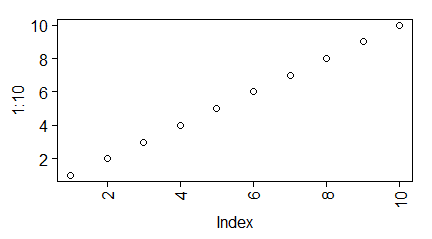
Orientację etykiet można zmienić za pomocą opcji las=n funkcji par() i innych funkcji graficznych. Wartościami tej opcji mogą być liczba całkowite od 0 do 3, które oznaczają:
- las=0 – poziomo przy osi poziomej, prostopadle przy osi pionowej (ustawienie standardowe),
- las=1 – poziomo przy obu osiach,
- las=2 – prostopadle przy obu osiach,
- las=3 – prostopadle przy osi poziomej, poziomo przy osi pionowej.
Można to zobaczyć na przykładzie:
| windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03, las=0) plot(1:10) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03, las=1) plot(1:10) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03, las=2) plot(1:10) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03, las=3) plot(1:10) |
Program powoduje powstanie 4 wykresów:
Dokładnie takie same wykresy powstaną, gdy opcja las=n zostanie zastosowane w nadrzędnej funkcji graficznej. Natomiast jej zastosowanie w funkcjach axis() dotyczy tylko tej osi, którą funkcja ta rysuje.
Czasami zamiast liczb na wykresach (zwłaszcza typu barplot() i boxplot()) chcemy umieścić wyjaśnienia. Służy do tego opcja labels=c() funkcji axis(), która jest ściśle związana z opcją at=c(). Myszą być wektorami o tej samej długości. Opcja at=c(), jak wcześniej wyjaśniono, umieszcza znaczniki w określonych miejscach i są nim przyporządkowywane odpowiednie liczby odczytywane ze współrzędnych pola kreślenia (a wyświetlane są tylko te, które mieszczą się na wykresie). Jeżeli jednak w funkcji axis() wystąpi opcja labels=c(), to etykiety liczbowe zostają zamienione na teksty występujące w tym ciągu. Oto trzy sposoby umieszczenia pod słupkami literowych oznaczeń w funkcji barplot():
Można to zobaczyć na przykładzie:
| windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) barplot(c(“A”=2, “B”=3, “C”=1)) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) a=barplot(c(2, 3, 1)) axis(1, at=a, labels=c(“A”, “B”, “C”)) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) a=barplot(c(2, 3, 1)) axis(1, at=c(0,a,a[3,1]+1), labels=c(“”,”A”, “B”, “C”,””)) |
Program generuje trzy następujące wykresy:
Gdy jest na to miejsce można w miejscu etykiety wstawić obszerniejsze wyjaśnienie:
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(3,1.5,0))
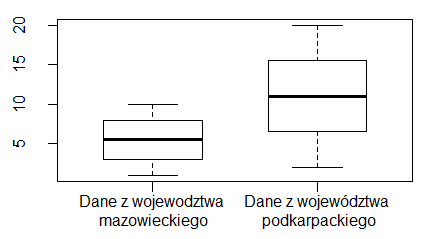
boxplot(1:10,2:20, boxwex=0.6)
axis(1,at=c(1,2), labels=c("Dane z wojewodztwa\n mazowieckiego",
"Dane z województwa\n podkarpackiego"))
|
Program ten spowoduje powstanie następującego wykresu:
Umiejscowienie i orientacja podpisów osi
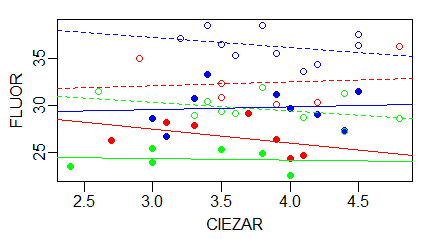
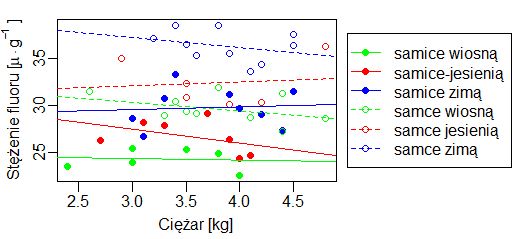
Podpisy osi są obowiązkowe we wszystkich wykresach związanych z opracowaniem danych. W biologii za brak podpisu choć jednej osi można dostać dwójkę (odpowiednik szkolnej pały). Tylko wtedy gdy etykiety na osiach jednoznacznie określają zmienną można sobie podpis odpuścić. Przykładowo gdy w miejscu etykiet występują słowa “samiec” i “samica” podpis osi typu “Płeć” może być pominięty, lecz, na przykład “Płeć szczurów wędrownych”, powinien już wystąpić.
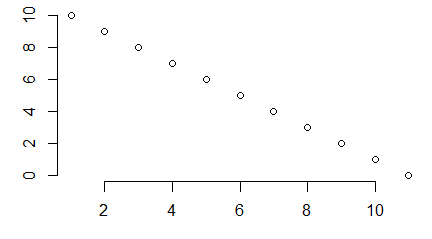
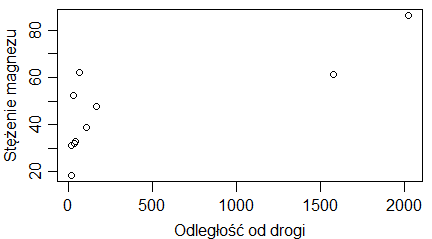
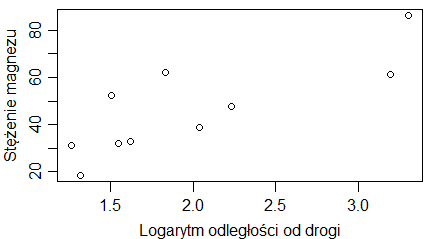
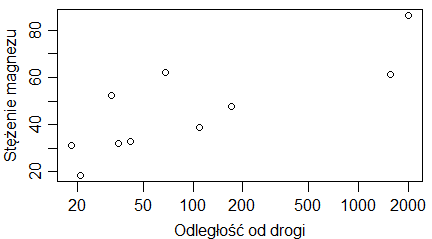
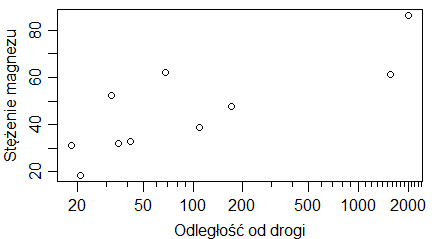
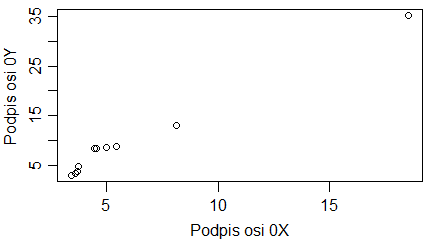
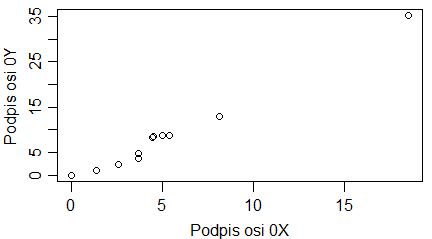
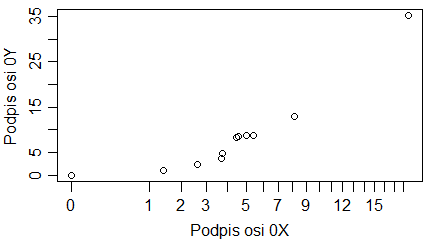
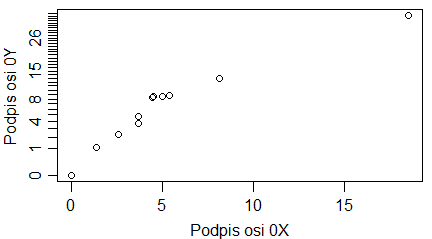
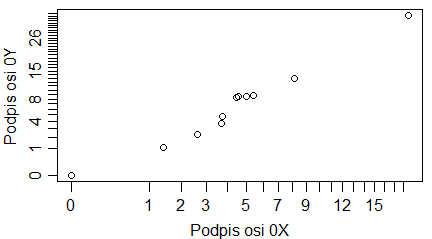
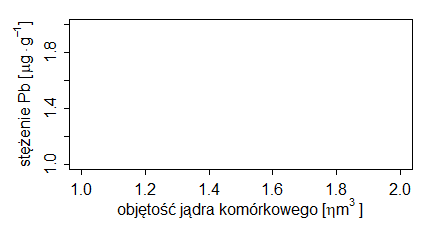
Podpisy osi dotyczą etykiet, które pojawiają się przy tej osi. Zatem na wykresach pokazujących średnie i odchylenia standardowe ciężarów samic i samców skunksów z Kolorado, podpis osi 0Y powinien brzmieć (ciężar [kg]), a nie (“średni ciężar [kg]”), bo na osi 0Y są ciężary i gdzieś między nimi mieści się średni ciężar. Podobne zasady dotyczą wykresów, których osie zostały zlogarytmowane. Gdy etykietami punktów są 0.1, 1, 10, 100, … (przedzielone czasem innymi liczbami) to są to niezlogarytmowane wartości ustawione na zlogarytmowanej osi. Wtedy w podpisie nie używamy słowa “zlogarytmowane …”. Natomiast gdy robimy wykres na zlogarytmowanych danych i na osi pokazują się liczby tworzące ciąg arytmetyczny – trzeba tego słowa użyć w popisie osi. Pokazują to wykresy utworzone przez następujący program:
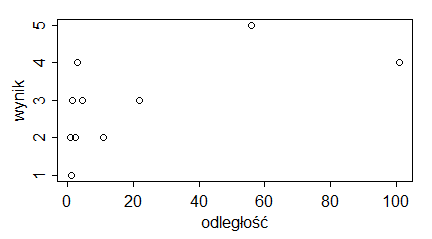
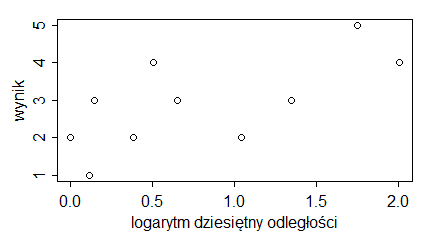
| odleglosc=c(1,1.3,1.4,2.4,3.2,4.5,11,22,56,101) wynik=c(2,1,3,2,4,3,2,3,5,4) windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) plot(odleglosc,wynik, xlab=”odległość”, ylab=”wynik”) # odleglosc=c(1,1.3,1.4,2.4,3.2,4.5,11,22,56,101) wynik=c(2,1,3,2,4,3,2,3,5,4) windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) plot(odleglosc,wynik, xlab=”odległość”, ylab=”wynik”, log=”x”) # odleglosc=c(1,1.3,1.4,2.4,3.2,4.5,11,22,56,101) wynik=c(2,1,3,2,4,3,2,3,5,4) windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(1.6,0.5,0), tck=-0.03) plot(log(odleglosc,10),wynik, xlab=”logarytm dziesiętny odległości”, ylab=”wynik”) |
Powstaną trzy wykresy z poprawnie podpisaną osią 0X.
Zazwyczaj podpis umieszcza się pod osią na marginesach. Można to jednak zmienić za pomocą opisanej już opcji mgp=c(z,y,x). Niestety stosuje się ona do obu osi jednocześnie. Gdy chcemy podpis jednej z osi umieścić wewnątrz pola kreślenia trzeba zastosować podrzędną funkcję graficzną text(), pozwalającą dopisywać teksty na wykresie (przede wszystkim w polu kreślenia).
Oto trzy programy pokazujące, jak tworzy się podpisy osi umiejscowione wewnątrz wykresu:
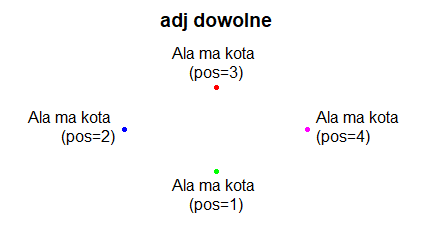
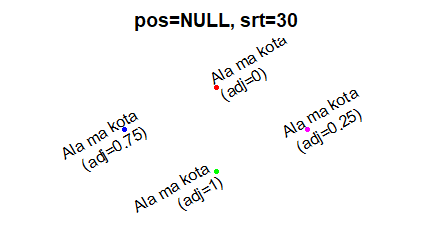
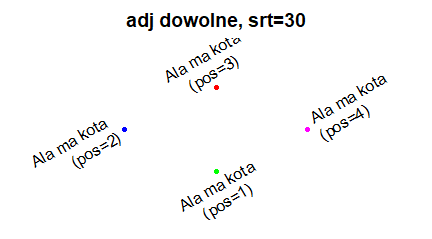
| windows(4.5, 2.5) par(mar=c(2,2,0.5,0.5), mgp=c(-1,0.5,0)) plot(1:10, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”) # windows(4.5, 2.5) par(mar=c(2,3,0.5,0.5), mgp=c(1.7,0.5,0)) plot(1:10, xaxt=”n”,xlab=””, ylab=”Podpis osi 0Y”) axis(1) text((par(“usr”)[1]+par(“usr”)[2])/2, 1.3, “Podpis osi 0X”) # windows(4.5, 2.5) par(mar=c(3,2,0.5,0.5), mgp=c(1.7,0.5,0)) plot(1:10, xlab=”Podpis osi 0X”, yaxt=”n”, ylab=””) axis(2) text(1, (par(“usr”)[3]+par(“usr”)[4])/2, srt=90, “Podpis osi 0Y”) |
Program tworzy trzy następujące wykresy:
Obowiązkowymi argumentami funkcji text() są współrzędne środka miejsca, gdzie będzie dopisany tekst. Te współrzędne dotyczą układu współrzędnych utworzonego w polu kreślenia. Opcja srt=x pokazuje kąt w stopniach o jaki ma być obrócony tekst zgodnie z ruchem wskazówek zegara.
Podpisy pod osiami domyślnie są wyśrodkowane. Czasem jednak umieszcza się je lewej lub prawej strony lub nieco przesuwa, gdy zasłaniają jakiś wyróżniony punkt. Można to zrobić dla obu osi stosując opcję adj=x w funkcji par() lub nadrzędnych funkcjach graficznych. Wartością tej opcji jest liczba z przedziału [0,1], gdzie:
- 0 oznacza wyrównanie do lewej (dla tekstów poziomych) i w dół (dla tekstów pionowych).
- 0.5 oznacza wyśrodkowanie
- 1 oznacza wyrównanie do prawej (dla tekstów poziomych) i w górę (dla tekstów pionowych)
- liczby pośrednie oznaczają przesunięcia w lewo, prawo albo w górę , dół w zależności od wartości liczby.
Wygląda to następująco:
| windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03, adj=0) plot(1:10, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03, adj=0.5) plot(1:10, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03, adj=1) plot(1:10, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03, adj=0.8) plot(1:10, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”) |
Program generuje cztery wykresy.
Gdy zmienia się wyrównanie tylko w jednej osi, należy jej podpis dopisać funkcją mtext() pozwalającą na dopisywanie tekstu na marginesach. Jej obowiązkową opcją jest dopisywany tekst w cudzysłowie, numer marginesu (side=n) i numer linijki (line=x), gdzie ma być wstawiony tekst. Opcja adj=x, wstawiona w tę funkcję, pokazuje jak wyrównany będzie tekst.
| windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03) plot(1:10, xlab=””, ylab=”Podpis osi 0Y”) mtext(“Podpis osi 0X”, 1,1.3, adj=0) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03) plot(1:10, xlab=””, ylab=”Podpis osi 0Y”) mtext(“Podpis osi 0X”, 1,1.3, adj=1) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03) plot(1:10, xlab=”Podpis osi 0X”, ylab=””) mtext(“Podpis osi 0Y”, 2,1.3, adj=0) # windows(4.5, 2.5) par(mar=c(2.5,2.5,0.5,0.5), mgp=c(1.5,0.5,0), tck=-0.03) plot(1:10, xlab=”Podpis osi 0X”, ylab=””) mtext(“Podpis osi 0Y”, 2,1.3, adj=1) |
Dzięki temu programowi powstają cztery wykresy:
Bardzo rzadko, ale może pojawić się potrzeba napisania podpisu pod osią pionową horyzontalnie ułożoną czcionką. Na dzień dzisiejszy nie wymyślono w R funkcji zmieniającej orientację poszczególnych liter w tekście, który sam ma nie zmienić pozycji. Zawsze można posłużyć się programem wpisującym poszczególne litery w normalnej pozycji, tylko jedna pod drugą. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(1.7, 0.5,0), tck=-0.03)
plot(0:7, xlab="Podpis osi 0X", ylab="", las=1)
par(xpd=TRUE)
a="Podpis osi 0Y"
b=nchar(a)
x=par("usr")[1]-0.8
dy=(par("usr")[4]-par("usr")[3])/b
for (i in 1:b) text(x,dy*(i-1), substr(a,b+1-i,b+1-i))
|
Program tworzy następujący wykres:
Przy innych danych zapewne należałoby poprawić współrzędne x i dy wskazujące miejsca poszczególnych liter. Zastosowana w programie opcja xpd=TRUE funkcji par() pozwala na dodawanie do wykresu różnych rzeczy poza polem kreślenia posługując się jego współrzędnymi.
Pozostałe sposoby modyfikowania osi związane są modyfikacją tekstu w różnych funkcjach graficznych i opisane zostały w rozdziale dotyczącym napisów, podpisów i tekstu.
Wspólne podpisy dla rycin złożonych z wielu wykresów
Najczęściej na rycinach złożonych z wielu wykresów umieszcza się wyniki badań, które w jakiś sposób porównuje się ze sobą. Na przykład, są wykonane dla dwóch różnych populacji, w różnych okresach za pomocą takich samych badań lub eksperymentów. Ich osie poziomą lub pionową, należy opisać tą samą frazą. Raczej nie powinno się tego rozbić pod każdym wykresem osobno. Odpowiedni podpis należy wstawić na marginesie “oma” i czasem sprawia to kłopoty. Podpis ten wstawia się za pomocą funkcji mtext() z jej opcjami side=n i line=n, tak jak wstawia się dodatkowe teksty na marginesach pojedynczego wykresu. Aby jednak pojawił się on na zewnętrznym marginesie, trzeba użyć dodatkowej opcji outer=TRUE. Poniższy program pokazuje jego działanie.
| windows(4.5,2.5) par(mar=c(1,3,0.5,0.5), mgp=c(1.8, 0.5, 0), mfrow=c(1,2),oma=c(2,0,0,0),xpd=NA) barplot(c(3,2,6,3,1,2), ylab=”Podpis osi 0Y”) barplot(c(3,2,6,3,1,2), ylab=””) mtext(“Wspólny podpis osi”,side=1,line=0.5) # windows(4.5,2.5) par(mar=c(1,3,0.5,1), mgp=c(1.8, 0.5, 0), mfrow=c(1,2),oma=c(2,0,0,0),xpd=NA) barplot(c(3,2,6,3,1,2), ylab=”Podpis osi 0Y”) barplot(c(3,2,6,3,1,2), ylab=””) mtext(“Wspólny podpis osi”,side=1,line=0.5,outer=TRUE) |
Na pierwszej rycinie podpis został zrobiony tylko do ostatniego wykresu na jego marginesie. Na drugim podpis jest na marginesie wspólnym.
Opcja outer=TRUE funkcji mtext() pozwala pisać na wszystkich czterech marginesach tworzonych przez opcje oma=c() w funkcji par(), co pokazuje następujący program:
windows(5,4)
par(mar=c(2,2,0.5,0.5), mfrow=c(2,2),oma=c(2,2,2,2),xpd=NA)
plot(c(1:6,6:1), xlab="", ylab="", main="")
plot(1:12, xlab="", ylab="", main="")
plot(12:1, xlab="", ylab="", main="")
plot(c(6:1,1:6), xlab="", ylab="", main="")
mtext("Wspólny podpis osi 0X",side=1,line=0.5,outer=TRUE)
mtext("Wspólny podpis osi 0Y",side=2,line=0.5,outer=TRUE)
mtext("Wspólny podpis osi dodatkowej 0X",side=3,line=0.5,outer=TRUE)
mtext("Wspólny podpis osi dodatkowej 0Y",side=4,line=0.5,outer=TRUE)
|
Efektem działania tego programu jest następujący wykres:
Osie logarytmiczne i transformowane funkcją rosnącą
W przypadku nierównomiernego rozmieszczenia wartości zmiennej (np. wiele wartości małych i kilka dużych) stosuje się przekształcenia normalizujące. Wartości zmiennej przekształca się funkcją F(x), rosnącą by interpretacja obserwowanych zależności nie zmieniała się. Jednym z najczęściej stosowanych przekształceń jest F(x)=log(x). Sposoby wykonania wykresu dla takich danych obrazuje następujący przykład:
Stężenie magnezu
62.14
38.69
47.72
61.35
86.03479
Odległość od drogi |
18.24 |
20.93 |
32.21 |
35.53 |
41.74 |
Stężenie magnezu |
31.28 |
18.65 |
52.54 |
31.82 |
32.84 |
Odległość od drogi |
68.40 |
109.05 |
171.55 |
1574.55 |
2023.56 |
Programy wykonujące wykresy mają postać:
x=c(18.24, 20.93, 32.21, 35.53, 41.74, 68.40, 109.05, 171.55, 1574.55, 2023.56)
y=c(31.28, 18.65, 52.54, 31.82, 32.84, 62.14, 38.69, 47.72, 61.35, 86.03479)
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Odległość od drogi", ylab="Stężenie magnezu", main="")
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(log(x,10),y, xlab="Logarytm odległości od drogi",
ylab="Stężenie magnezu", main="")
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Odległość od drogi", ylab="Stężenie magnezu", main="", log="x")
|
Zależność między odległością od drogi a stężeniem magnezu możemy pokazać na trzy sposoby:
Pierwszy z wykresów pokazuje zasadność zlogarytmowania odległości. Drugi i trzeci są takie same – różnią się tylko etykietami na osi poziomej. Ponieważ podpis osi ma wskazywać czym są liczby umieszczone jako etykiety, gdy sami logarytmujemy dane musimy to zaznaczyć w opisie osi. Gdy stosujemy opcję log=”x” mamy wprawdzie nierównomiernie rozmieszczone znaczniki, ale etykiety oznaczają odległości, nie logarytmy odległości. Inaczej zatem podpisujemy tę oś.
Czasami na zlogarytmowanej osi chciałoby się dorysować znaczniki. Podkreśla to, że mamy do czynienia z danymi transformowanymi. Można to zrobić dodając funkcję axis() w następującej formie:
x=c(18.24, 20.93, 32.21, 35.53, 41.74, 68.40, 109.05, 171.55,
1574.55, 2023.56)
y=c(31.28, 18.65, 52.54, 31.82, 32.84, 62.14, 38.69, 47.72, 61.35, 86.03479)
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Odległość od drogi", ylab="Stężenie magnezu",
main="", log="x")
axis(1, at=(0:10)*10, labels=rep("",11), tck=-0.03)
axis(1, at=(1:25)*100, labels=rep("",25), tck=-0.03)
|
Powstanie następujący wykres:
Opcja log może przyjmować wartość
"x"
, gdy chcemy mieć zlogarytmowane wartości na osi poziomej, wartość
"y"
, gdy chcemy mieć zlogarytmowane wartości na osi pionowej oraz wartość
"xy"
gdy chcemy mieć zlogarytmowane obie osie.
x=c(3.39, 3.58, 3.68, 3.71, 4.45, 4.55, 5.00, 5.42, 8.14, 18.56)
y=c(3.02, 3.29, 3.64, 4.79, 8.29, 8.46, 8.65, 8.76, 12.95, 35.10)
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="")
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="", log="x")
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="", log="y")
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
plot(x,y, xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="",log="xy")
|
Opcja log występuje także w funkcjach barplot() i boxplot(). Stosuje się jednak ona tylko do danych liczbowych dodatnich.
x=c(3.39, 3.58, 3.68, 3.71, 4.45, 4.55, 5.00, 5.42, 8.14, 18.56)
y=c(3.02, 3.29, 3.64, 4.79, 8.29, 8.46, 8.65, 8.76, 12.95, 35.10)
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
barplot(rbind(x,y), xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="",
log="y", xpd=FALSE)
windows(4.5,2.5)
par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0))
boxplot(x,y, xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="", log="y")
|
Wszelkie obliczenia wykonywane przez funkcje barplot() i boxplot() odbywają się na zlogarytmowanych danych.
Opcja log zmienia pole kreślenia w taki sposób, że kolejne liczby pojawiają się w odległościach zlogarytmowanych. Ułatwia to umiejscowienie elementów dorysowywanych przez podrzędne funkcje graficzne.
Nie zawsze do wyrównania odległości między danymi stosuje się funkcję logarytm dziesiętny. Gdy na przykład wiele wartości zmiennej ma wartość 0 i tylko pewne z nich są dodatnie, dobrą transformację danych daje funkcja pierwiastek (czasem pierwiastek wyższego stopnia itd.). Czasami stosuje się transformację Box-Coxa w celu znormalizowania danych, czyli takiego ich przekształcenia, aby można było dla nich wykonać najmocniejsze testy statystyczne. Jest to transformacja postaci:
![]()
gdzie λ dobiera się do danych.
Jak dla innych transformacji danych niż logarytmiczna, dostosować osie tak, by nie trzeba było zmieniać ich podpisów? Postępujemy według następującego schematu:
- Przekształcamy dane (np funkcją T(x)).
- Robimy wykres dla przekształconych danych bez rysowania osi (tej lub tych dla których zastosowano transformację).
- Dorysowujemy oś ze znacznikami w odległościach T(1:x) z etykietami 1:x.
Wygląda to następująco:
| x=c(0, 1.39, 2.58, 3.68, 3.71, 4.45, 4.55, 5.00, 5.42, 8.14, 18.56) y=c(0, 1.02, 2.29, 3.64, 4.79, 8.29, 8.46, 8.65, 8.76, 12.95, 35.10) # windows(4.5,2.5) par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0)) plot(x,y, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”, main=””) # windows(4.5,2.5) par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0)) plot(sqrt(x),y, xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”, main=””, axes=FALSE) axis(1, at=sqrt(0:18), labels=0:18 ) axis(2) box() # windows(4.5,2.5) par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0)) plot(x,sqrt(y), xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”, main=””, axes=FALSE) axis(1) axis(2, at=sqrt(0:36), labels=0:36) box() # windows(4.5,2.5) par(mar=c(3,3,0.5,0.5), mgp=c(2,0.7,0)) plot(sqrt(x),sqrt(y), xlab=”Podpis osi 0X”, ylab=”Podpis osi 0Y”, main=””, axes=FALSE) axis(1, at=sqrt(0:18), labels=0:18 ) axis(2, at=sqrt(0:36), labels=0:36) box() |
Tworzenie wykresów z osiami przekształconymi funkcją nieliniową jest w R prostsze, niż w jakimkolwiek innym programie.
Kolory
Kodowanie kolorów
R wykorzystuje wszystkie możliwe kolory istniejące w systemach cyfrowych. Listę dostępnych kolorów można uzyskać za pomocą komendy colors(). Są to angielskie nazwy różnych kolorów, niektóre z cyframi na końcu, ujęte w cudzysłów. Z reguły cyfry na końcu im są wyższe tym kolor jest ciemniejszy. Liczba tych kolorów zależy od systemu operacyjnego i wersji R, i przeważnie jest ich kilkaset. Na pierwszy miejscu jest “white”, ale później nazwy kolorów wymieniane są w porządku alfabetycznym. Początek tej listy wygląda następująco:
> colors()
[1] "white" "aliceblue" "antiquewhite" "antiquewhite1"
[5] "antiquewhite2" "antiquewhite3" "antiquewhite4" "aquamarine"
[9] "aquamarine1" "aquamarine2" "aquamarine3" "aquamarine4"
[13] "azure" "azure1" "azure2" "azure3"
[17] "azure4" "beige" "bisque" "bisque1"
[21] "bisque2" "bisque3" "bisque4" "black"
|
Wypisywanie długich angielskich nazw w programach może być męczące. Dlatego ostre podstawowe kolory można uzyskać za pomocą liczb zapisywanych już nie w cudzysłowie. Lista odpowiadających im kolorów znajduje się poniżej.
- 0 – biały
- 1 – czarny
- 2 – czerwony
- 3 – zielony
- 4 – niebieski
- 5 – jasnoniebieski
- 6 – różowy
- 7 – żółty
- 8 – szary
Potem, przy wzroście liczby (9,10,11,…) kolory od 1 do 9 (bez białego) powtarzają się.
Kolory można zapisywać w systemie RGB. Nazwy takiego koloru składają się z 7 znaków. Pierwszym z nich jest “#”, kolejne sześć znaków tworzą liczbę zapisaną w systemie szesnastkowym. Są to współrzędne punktu odczytane z tzw. sześcianu kolorów. Dwa pierwsze znaki oznaczają nasycenie kolorem czerwonym, kolejne dwa – nasycenie kolorem zielonym a piąty i szósty znak – kolorem niebieskim. R stosuje także nieco zmodyfikowany zapis kolorów w systemie RGB składający się z 9 znaków. Po znaku “#” kolejne sześć znaków oznacza stopnie nasycenia kolorami czerwonym, zielonym i niebieskim, zaś ostatnie dwa znaki – liczba w systemie szesnastkowym – stopień nie przeźroczystości. Na białym tle barwne figury stają się coraz jaśniejsze, gdy liczba ta jest coraz mniejsza. Domyślna wartość FF daje kolor całkiem nie przeźroczysty.
Kody te wyglądają następująco “#f5cc23”, “#AB7C3F” itp. Mogą być w nich cyfry i litery od a do f. W R jest wszystko jedno czy te litery napiszemy jako duże czy małe.
Listy kolorów zapisywanych w systemie RGB znajdują się w Internecie na wielu stronach, np. albo https://www.w3schools.com/colors/colors_rgb.asp. Można je znaleźć także w Wikipedii pod hasłem “lista kolorów”.
Symbole kolorów w notacji RGB można uzyskać za pomocą funkcji rgb(), której trzy pierwsze argumenty określają nasycenie koloru barwą czerwoną, niebieską i zieloną, a czwarty określa przeźroczystość. Domyślnie wszystkie cztery liczby mają wartości z przedziału [0,1]. Ponieważ w wielu programach, system RBG pozwala na wybieraniu nasycenia kolorami podstawowymi za pomocą liczb całkowitych od 0 do 255, funkcja rgb() ma opcję maxColorValue=255, która pozwala na właśnie taki sposób na wybieranie koloru. Wygląda to następująco:
> rgb(0.5, 0.5, 0.5, 0.5)
[1] "#80808080"
> rgb(100, 200, 10, 70, maxColorValue=255)
[1] "#64C80A46"
|
Inną przydatną funkcją do sterowania kolorami jest col2rgb(), która dla danego koloru tworzy wektor (a właściwie jednokolumnową macierz) pokazującą stopień nasycenia kolorami czerwonym, zielonym i niebieskim (liczby od 0 do 255).
> col2rgb("#FFCC11")
[,1]
red 255
green 204
blue 17
> col2rgb("lightblue")
[,1]
red 173
green 216
blue 230
|
Warto przy tym zapamiętać regułę: kolor “#uvwxyz” jest taki sam jak “#uvwxyzFF”, a liczby w systemie szesnastkowym mniejsze od FF napisane na końcu dają kolor o tej samej barwie co “#uvwxyz” tylko jaśniejszy, ogólnie podobniejszy do tła.
Bywa, że musimy znaleźć kod koloru w systemie HSV, gdy znamy go w RGB. Do konwersji służy funkcja rgb2hsv(). Argumentami tej funkcji są stopnie wysycenia kolorami czerwonym, zielonym i niebieskim oraz maksymalna liczba określająca te wysycenia (domyślnie 255), a wynikami odcień (ang. hue), nasycenie (ang. saturation) i wartość (ang. value) będące liczbami od 0 do 1. Funkcja hsv() zamienia ten ciąg na kod RGB.
> rgb2hsv(100,50,120)
[,1]
h 0.7857143
s 0.5833333
v 0.4705882
> hsv(0.7857143,0.5833333,0.4705882)
[1] "#643278"
|
Wielkim ułatwieniem dla programistów jest możliwość automatycznego wyboru ciągu kilku kolorów skrajnie różniących się od siebie. Są to funkcja rainbow() i gray(). Pierwsza z tych funkcji wybiera kolory z palety barw nasyconych ułożonych w tęczę i jej argumentem jest liczba wybieranych kolorów. Druga funkcja ogranicza się do różnych odcieni szarości i jej argumentem jest wektor nasyceń kolorem czarnym (od 0 – biały do 1 – czarny), czy jeśli patrzymy na ekran, a nie drukarkę – stopiej nasycenia pikseli światłem.
> rainbow(7)
[1] "#FF0000FF" "#FFDB00FF" "#49FF00FF" "#00FF92FF" "#0092FFFF"
[2] "#4900FFFF" "#FF00DBFF"
> gray(1:7/10)
[1] "#1A1A1A" "#333333" "#4D4D4D" "#666666" "#808080"
[2] "#999999" "#B3B3B3"
|
R zapewnia nam dostęp do wszystkich kolorów, nawet gdy nie ma ich nasz monitor. Sterownik graficzny dobierze kolor najbardziej podobny do wybranego.
Kolor tła
Do prac dyplomowych nadaje się właściwie tylko kolor biały jako kolor tła wykresu. Jest to kolor domyślny. Nie mniej w przypadku wykonywania posterów lub prezentacji często stosowany jest inny kolor, by dopasować grafikę wykresów do stylu całego opracowania. Kolor tła zmieniamy za pomocą parametrów bg=”color”, funkcji par().
windows(4.5, 2.5)
par(mar=c(3,3,1,1), bg="#99ccff")
plot(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), bg="#99ff99")
pie(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), bg="#ccff33")
barplot(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), bg="#ffcccc")
boxplot(1:10)
|
Powstaną w taki sposób cztery wykresy:
Takie ustawienia pamiętane będą przez R i wykonywane dopóki nie zostaną zmienione nową funkcją par(bg=””).
Kolor tła pola kreślenia
Nadrzędne funkcje graficzne w bibliotece graphics nie mają opcji zmiany koloru tła samego pola kreślenia. Tymczasem takie wykresy często umieszcza się na posterach i w prezentacjach. Z reguły marginesy są ciemniejsze od tła pola kreślenia. Jest to eleganckie oddzielenie wyników badań od wyjaśnień i komentarzy. W R trzeba sobie poradzić za pomocą swojego rodzaju “oszustwa”. Oszustwa w stosunku do programów, które takie kolorowanie tła pola kreślenia umożliwiają. Polega ono na:
- Utworzeniu wykresu za pomocą funkcji graficznej rysującej z odpowiednimi marginesami i ustalonymi opcjami zmieniającymi współrzędne pola kreślenia, ale bez obiektów wpisywanych w pole kreślenia.
- Utworzeniu prostokąta o współrzędnych odczytanych z funkcji par(“usr”) i odpowiednim kolorze wypełnienia.
- Wpisaniu do wykresu tego wszystkiego, co ma być w polu kreślenia.
Nie jest to aż tak pracochłonne, jak to wygląda. Pierwsza z funkcji graficznych rysujących tworzy odpowiednie marginesy i wyznacza pole kreślenia. Daje też odpowiednie tło całości. Jest ono zamalowywane przez prostokąt zajmujący całe pole kreślenia. Na końcu na tym prostokącie kreślone jest to, co powinno być zrobione przez nadrzędną funkcję graficzną, tyle że przez odpowiednią funkcję podrzędną. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#99ccff")
plot(1:10,type="n")
rect(par("usr")[1], par("usr")[3], par("usr")[2], par("usr")[4], col="#aaddff")
points(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#ccff33")
barplot(1:10)
rect(par("usr")[1], par("usr")[3], par("usr")[2], par("usr")[4], col="#e6fac8")
barplot(1:10,add=TRUE)
#
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#ffcccc")
boxplot(1:10,type="n")
rect(par("usr")[1], par("usr")[3], par("usr")[2], par("usr")[4], col="#ffecf1")
boxplot(1:10,add=TRUE)
|
Program ten tworzy następujące wykresy:
W podobny sposób możemy “oszukać” komputer używając podrzędnej funkcji graficznej grid(), co pozwala na rezygnację z używania liczb pojawiających się w wektorze par(“usr”). Jest to funkcja standardowo dokładająca siatkę na wykresie. Niestety siatka ta nie pojawia się pod danymi, ale na nich, co powoduje, że często trzeba dane ponownie narysować. Siatkę można utworzyć z gęsto narysowanych grubych linii ciągłych o określonym kolorze. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#99ccff")
plot(1:10,type="n")
grid(100,50, col="#aaddff", lty=1, lwd=10)
points(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#ccff33")
barplot(1:10)
grid(100,50, col="#e6fac8", lty=1, lwd=10)
barplot(1:10,add=TRUE)
#
windows(4.5, 2.5)
par(mar=c(3,3,0.5, 0.5), mgp=c(1.7,0.5,0), tck=-0.03, bg="#ffcccc")
boxplot(1:10,type="n")
grid(100,50, col="#ffecf1", lty=1, lwd=10)
boxplot(1:10,add=TRUE)
|
Powstaną w ten sposób następujące trzy wykresy:
Są one bardzo podobne do poprzednich, tylko niektórym przydałoby się obramowanie zrobione np. funkcją box().
Jedyną funkcją, z która tego typu manipulacja nie jest wykonalna, to funkcja pie(). Nie ma ona bowiem opcji zamieniającej jej na funkcje graficzną dokładającą. Jedyny sposób polega na samodzielnym wykonaniu wielokątów mających kształt wycinka koła o odpowiednik kącie wierzchołkowym i położeniu, a nie jest to wcale takie proste, bo wśród istniejących w pakiecie graphics funkcji graficznych dokładających, nie ma wycinków kół. Nie mniej w rozdziale 10 podano kod takiej funkcji i sposób jej wykorzystania do zrobienia ładnych wykresów kołowych na kolorowym tle.
Kolor kreślenia
W polu kreślenia sam wykres, a dokładnie jego kontury, są rysowane domyślnie kolorem czarnym. To także najlepszy kolor dla wykresów umieszczanych w pracach dyplomowych, gdzie co najwyżej wypełnienia słupków lub pudełek robi się kolorowe. Nie mniej można to zmienić opcją fg=”kolor” wstawianej do funkcji par() lub do odpowiednich nadrzędnych funkcji graficznych.
windows(4.5, 2.5)
par(mar=c(3,3,1,1), fg="blue")
plot(1:10)
#
windows(4.5, 2.5)
par(mar=c(1,3,1,1), fg="red")
pie(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), fg="green")
barplot(1:10)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), fg="brown")
boxplot(1:10)
|
Powstaną w taki sposób cztery wykresy:
Jak widać opcja ta zmienia kolor także osi i znaczników, a w funkcji pie() – etykiet wykresu.
Kolory elementów wykresu
Przy opracowaniu graficznym wyników badań z reguły kolorów używa się do wskazania odrębnych grup danych. Powoduje to, że elementy pojawiające się w polu kreślenia powinny mieć różne kolory. R umożliwia to, bowiem argumentem podstawowej opcji wskazującej kolor col=c() poszczególnych elementów wykresu może być wektor różnych kolorów. Pierwszy element wykresu będzie miał pierwszy kolor, drugi kolor, itd. Gdy elementów wykresu jest więcej niż kolorów, cykl przyznawania kolorów powtarza się.
windows(4.5, 2.5)
par(mar=c(3,3,1,1))
plot(1:10, col=rainbow(20)[1:5*3])
#
windows(4.5, 2.5)
par(mar=c(1,3,1,1))
pie(1:10, col=rainbow(20)[3:8*2])
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1))
barplot(1:10, col=rainbow(20)[11:15])
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1))
boxplot(1:10, 2:11, 3:12, 4:13, 5:14, 1:10, 2:11, 3:12, 4:13, 5:14,
col=rainbow(20)[16:20])
|
Program tworzy 4 wykresy:
Opcja col=c() w taki sam sposób działa także w wielu podrzędnych funkcjach graficznych.
Kolory osi
Wśród opcji graficznych związanych z kolorowaniem wykresu jest opcja col.axis=”kolor”. Zmienia ona jedynie kolor etykiet na wykresie. Opcja col.lab=”kolor” zmienia kolor podpisów pod osiami.
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
plot(1:10, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.axis=2, col.lab=3)windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
barplot(1:10, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.axis=3, col.lab=4)windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
boxplot(1:10, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.axis=4, col.lab=2)
|
Program utworzy następujące wykresy:
Kolor samej osi możemy zmienić dopiero używając funkcji axis() do ich narysowania. Opcją, która to robi jest col=”kolor”.
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
plot(1:10, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.lab=4)
axis(1, at=0:5*2, col=2, col.axis=3)
axis(2, at=0:5*2, col=3, col.axis=2)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
barplot(1:10, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.lab=3)
axis(2, at=0:5*2, col=2, col.axis=4)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
boxplot(1:10, axes=FALSE, xlab="Podpis osi 0X", ylab="Podpis osi oY",
col.lab=2)
box(col=3)
axis(2, at=0:5*2, col=4, col.axis=5)
|
Program generuje 3 wykresy:
Odpowiednie opcje pozwalają także kolorować wszelkie napisy i podpisy wprowadzane do wykresu. Za tytuł odpowiada opcja col.main=”kolor”, za podpis odpowiada opcja col.sub=”kolor”. Ponadto opcja col=”kolor” umieszczona w funkcjach title(), text() i mtext() tworzy napisy odpowiedniego koloru.
Wzory, desenie, tekstura i siatka
Znaczniki
Znaczniki, jako graficzna reprezentacja punktów na wykresach występują w funkcjach plot() i matplot() z opcją type=”p” lub type=”b” oraz w funkcji points(). Standardowo pojawiają się w wykresach jako puste kółeczka. Można zmienić ich kształt wykorzystując opcje pch=n, gdzie n jest liczbą od 1 do 25 generującą różne kształty znaczników. Można je zobaczyć za pomocą programu:
windows(4.5, 2.5)
par(mar=c(1,1,1,1), xpd=TRUE)
plot(1:5, type="n", axes=FALSE)
points(1:5, rep(5,5), pch=1:5)
points(1:5, rep(4,5), pch=6:10)
points(1:5, rep(3,5), pch=11:15)
points(1:5, rep(2,5), pch=16:20)
points(1:5, rep(1,5), pch=21:25)
text(1:5+0.2, rep(5,5), paste(1:5))
text(1:5+0.2, rep(4,5), paste(6:10))
text(1:5+0.2, rep(3,5), paste(11:15))
text(1:5+0.2, rep(2,5), paste(16:20))
text(1:5+0.2, rep(1,5), paste(21:25))
|
Powstaje w ten sposób wykres:
Wielkość znacznika można zmienić opcją cex=x. Standardowo cex=1. Można mu przypisywać wartości typu ciąg liczb, co daje ciekawe efekty.
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:10, type="p", pch=c(8,20), cex=1:10/2)
|
Program generuje wykres:
Kolory znaczników można zmienić opcją col=c(“color1”, “color2”,…). Dopasowuje ona punkt na pozycji i-tej z kolorem na pozycji i-tej, a gdy kolorów jest mniej niż punktów proces dopasowania zaczyna się do początku wektora kolorów. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(1,1,1,1), xpd=TRUE)
matplot(1:5, cbind(1:5, 1:5*2, 1:5*3),type="b", pch=19, col=rainbow(3))
|
Program generuje pokazany niżej wykres.
W funkcji matplot() zawsze ten sam znacznik, kolor i wielkość dopasowywany jest do całej serii danych zapisanych w kolumnach macierzy wyników.
Linie
Linie pokazują się jako wyniki w wykresach liniowych, ale są też obramowaniami słupków lub pudełek. Ponadto występują na osiach i obramowaniach wykresu, a często też trzeba dodać jakąś linię lub łamaną do wykresu. We wszystkich funkcjach rysujących linie, ich styl można zmienić za pomocą opcji lty=n mającą wartości od 1 do 6. Zamiast liczb można wpisać nazwy wzorów:
- “solid” Linia ciągła ustalana domyślnie.
- “dashed” Linia kreskowana.
- “dotted” Linia kropkowana.
- “dotdashed” Linia kreskowano-kropkowana.
- “longdashed” Linia kreskowana z długini kreseczkami.
- “twodashed” Linia zmiennie kreskowana krótkimi i długimi kreskami.
Można je zobaczyć za pomocą programu:
windows(4.5, 2.5)
par(mar=c(1,1,1,1), xpd=TRUE)
plot(1:9, type="n", axes=FALSE)
for (i in 1:9) {lines(c(1,8), c(10-i,10-i), lty=i)
text(9,10-i,paste("lty =",i))}
|
Po jego uruchomieniu pokazuje się następujący wykres:
Dla lty=7 linia ma taki sam styl jak lty=1 , lty=8 odpowiada lty=2 itp.
W funkcji matplot() opcja lty=n może mieć wartości zapisane w postaci wektora. Każda z linii otrzyma wtedy styl ustalony według zasady n-ty numer kolumny w macierzy wyników ma styl zapisany na n-tym miejscu w tym wektorze (który ewentualnie jest wielokrotnie powielany). Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(1,1,1,1), xpd=TRUE)
matplot(1:5, cbind(1:5, 1:5*2, 1:5*3, 1:5*4, 1:5*5, 1:5*6), type="l",
lty=1:3)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1), xpd=TRUE)
matplot(1:5, cbind(1:5, 1:5*2, 1:5*3, 1:5*4, 1:5*5, 1:5*6), type="l",
lty=c(1,1,2,2,3,3))
|
Grubość linii określa się opcją lwd=x, gdzie x musi być większe od 0, choć może mieć wartość NA (brak linii). Wygląd linii o grubości x na różnych monitorach może nieco różnić sie od siebie i najlepiej jest przetestować to za pomocą programu:
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:10, type="n", axes=FALSE, main="lty=1")
for (i in 1:10){ lines(c(1,8), c(11-i,11-i), lwd=i, lty=1)
text(10,11-i, paste(i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:10, type="n", axes=FALSE, main="lty=2")
for (i in 1:10){ lines(c(1,8), c(11-i,11-i), lwd=i, lty=2)
text(10,11-i, paste(i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:10, type="n", axes=FALSE, main="lty=3")
for (i in 1:10){ lines(c(1,8), c(11-i,11-i), lwd=i, lty=3)
text(10,11-i, paste(i))}
|
Po jego uruchomieniu pojawią się trzy wykresy:
Przy grubych liniach widać, że końce linii są zaokrąglone. Zmianę kształtu końców linii można uzyskać za pomocą opcji lend=n mającą wartości 0, 1 lub 2 albo ich odpowiednik słowny:
- “round” = 0 końce zaokrąglone (wartość domyślna)
- “butt” = 1 końce kwadratowe przez obcięcie zaokrągleń.
- “square” = 2 końce kwadratowe przez objęcie zaokrągleń.
Różnice po uzyciu tej opcji widać
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6, type="n", axes=FALSE, main="lend=0")
for (i in 1:6){ lines(c(1,5.5), c(7-i,7-i), lwd=10, lend=0, lty=i)
text(6,7-i, paste("lty=",i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6, type="n", axes=FALSE,, main="lend=1")
for (i in 1:6){ lines(c(1,5.5), c(7-i,7-i), lwd=10, lend=1, lty=i)
text(6,7-i, paste("lty=",i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6, type="n", axes=FALSE, main="lend=2")
for (i in 1:6){ lines(c(1,5.5), c(7-i,7-i), lwd=10, lend=2, lty=i)
text(6,7-i, paste("lty=",i))}
|
Program spowoduje powstanie trzech wykresów:
Również sposób łączenia linii w krzywych łamanych można zmienić opcją ljoin=n, gdzie n ma wartość 0, 1 lub 2 albo słowną:
- “round” = 0 połaczenia zaokrąglone (wartość domyślna)
- “mitre” = 1 połaczenia stożkowe.
- “bevel” = 2 połaczenia będące ściętym stożkiem.
x=c(0,3,2,5,3,4)
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6,1:6*2, type="n", axes=FALSE, main="lend=0, ljoin=0", xlim=c(1,7))
for (i in 1:6){ lines(1:6, x+7-i, lwd=10, lend=0, ljoin=0, lty=i)
text(7,7-i+4, paste("lty=",i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6,1:6*2, type="n", axes=FALSE, main="lend=0, ljoin=1", xlim=c(1,7))
for (i in 1:6){ lines(1:6, x+7-i, lwd=10, lend=0, ljoin=1, lty=i)
text(7,7-i+4, paste("lty=",i))}
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), xpd=TRUE)
plot(1:6,1:6*2, type="n", axes=FALSE, main="lend=0, ljoin=2", xlim=c(1,7))
for (i in 1:6){ lines(1:6, x+7-i, lwd=10, lend=0, ljoin=2, lty=i)
text(7,7-i+4, paste("lty=",i))}
|
Program generuje trzy wykresy:
Operowanie opcjami lend i ljoin niekiedy zwiększa optycznie zróżnicowanie linii na wykresach, co ułatwia jego interpretację.
Niekiedy wybrane nadrzędne funkcje graficzne w nieoczekiwany sposób reagują na opcję lty=n. Np. w funkcji barplot() nie zmienia się styl obramowań słupków, ale istnieje opcja axis.lty=n, która zmienia styl osi pionowej. W funkcjach pie() i boxplot() opcja ta zmienia obramowania wycinków koła i pudełek, a także styl prostej oznaczającej medianę. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
barplot(1:10, lty=2, axis.lty=3)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
boxplot(1:10, lty=2)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
pie(1:10, lty=2)
|
Dzięki temu programowi powstają wykresy:
Desenie i tekstura
W standardowych opcjach R nie istniej coś takiego, jak wypełnianie obszaru zadanym wcześniej wzorem lub robieniu wykresu na tle zdjęcia. Możemy co najwyżej wypełnić wzorami to, co jest możliwe do wypełnienia kolorem. Są to słupki w funkcji barplot(), wycinki koła w funkcji pie() oraz wielokąty napisane funkcją graficzna dokładającą polygon(). Zrobienie wzorów umożliwiają opcje density=x, angle=y. Powodują one wpisanie w obszary kresek o nachyleniu y (y oznacza kąt w stopniach) i zagęszczeniu x. W domyśle x=NULL, co daje efekt braku tekstury.
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
pie(c(4,2,3,5,1,2), angle=1:6*30, density=10)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
barplot(c(4,2,3,5,1,2), angle=1:6*30, density=10)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:6, type="n")
polygon(1:6, c(4,2,3,5,1,2), angle=30, density=10)
|
Wykonanie tych funkcji powoduje wygenerowanie trzech wykresów:
Dodatkowe efekty daje możliwość kolorowania tekstury, wybierania wzorów i grubości linii tworzących teksturę oraz nakładania wykresów na siebie (nie dotyczy funkcji pie()):
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
pie(c(4,2,3,5,1,2), angle=1:6*30, density=1:6*20, lty=1:6, lwd=5, col=1:6)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
barplot(c(4,2,3,5,1,2), angle=1:6*30, density=1:6*5, col=1:6)
barplot(c(4,2,3,5,1,2), angle=1:6*(-30), density=1:6*5, col=1:6, add=TRUE)
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:6, type="n")
polygon(1:6, c(4,2,3,5,1,2), angle=30, density=20, lty=3, col=3)
polygon(1:6, c(4,2,3,5,1,2), angle=-30, density=30, lty=3, col=7)
polygon(1:6, c(4,2,3,5,1,2))
|
Wynikiem działania tego programu są trzy wykresy wyglądające następująco:
Siatka w polu kreślenia
Czasem z wykresów trzeba odczytywać przybliżone wartości danych i bardzo pomaga w tym siatka umieszczana w polu kreślenia. Umieszcza się ją stosując podrzędną funkcję graficzną grid(), której przykład zastosowania podano już w rozdziale o kolorach jako sposób na kolorowanie tła pola kreślenia. Jej użycie dla różnych typów wykresów wygląda następująco:
windows(4.5, 2.5)
par(mar=c(2,2,1,1))
plot(c(4,2,3,5,1,2))
grid()
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
pie(c(4,2,3,5,1,2))
grid()
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1))
barplot(c(4,2,3,5,1,2))
grid()
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1))
boxplot(1:6)
grid()
|
Widać, że siatka tworzy się na wykresie, a nie w tle. Powoduje to często konieczność nadpisania wykresu funkcjami graficznymi dokładającymi (co nie jest możliwe dla funkcji pie(). Wygląda to wtedy następująco:
windows(4.5, 2.5)
par(mar=c(2,2,1,1))
plot(c(4,2,3,5,1,2))
grid(col="#ccffff", lty=1, lwd=2)
points(1:6,c(4,2,3,5,1,2))
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1))
barplot(c(4,2,3,5,1,2))
grid(col="#ffccff", lty=1, lwd=2)
barplot(c(4,2,3,5,1,2),add=TRUE)
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1))
boxplot(1:6)
grid(col="#ccffcc", lty=1, lwd=2)
boxplot(1:6, col="white", add=TRUE)
|
Program utworzy wykresy:
Opcje graficzne takie jak col=”kolor”, lty=n, lwd=x umożliwiają tworzenie różnych wzorów i kolorów linii stosowanych w siatce i nie sprawiają one problemów. Problemem jest inne niż domyślne rozmieszczenie linii siatki tak, aby spełniała ona swoje zadanie, tzn. umożliwiała odczytywanie na osiach wartości. Chodzi o opcje nx=n i ny=n wskazujące, z ilu linii poziomych i pionowych ma składać się siatka. Po policzeniu tych części na wyżej wykonanych wykresach i wstawieniu ich do opcji nx=n i ny=n otrzymamy następujący program:
| windows(4.5, 2.5) par(mar=c(2,2,1,1)) plot(c(4,2,3,5,1,2)) grid(nx=7, ny=6, col=”#ccffff”, lty=1, lwd=2) points(1:6,c(4,2,3,5,1,2)) # windows(4.5, 2.5) par(mar=c(1,2,1,1)) barplot(c(4,2,3,5,1,2)) grid(nx=9, ny=5, col=”#ffccff”, lty=1, lwd=2) barplot(c(4,2,3,5,1,2),add=TRUE) # windows(4.5, 2.5) par(mar=c(1,2,1,1)) boxplot(1:6) grid(nx=6, ny=7, col=”#ccffcc”, lty=1, lwd=2) boxplot(1:6, col=”white”, add=TRUE) |
który generuje następujące wykresy:
Siatki, których linie nie wypadają w znacznikach etykiet osi, nie tylko nie ułatwiają odczytanie wartości danych, ale też niezbyt ładnie wyglądają. Winna jest temu zasada dzielenia całego obszaru kreślenia na równe części łącznie z 4% dodatkiem wydłużającym z każdej strony obszar kreślenia. Wykres barplot() dla osi 0Y tego nie robi i linie siatki są na nim poprawne. Jak sobie z poradzić z innymi wykresami? Są na to trzy sposoby:
- nx=NULL, ny=NULL powoduje, że linie siatki są wykreślane zgodnie z podanymi znacznikami osi utworzonymi domyślnie.
- nx=NA, ny=NA powoduje, że odpowiednie linie pionowe albo poziome siatki nie pojawią się.
- Zastosowanie opcji xax=”i”, yaxs=”i” oraz xlim=c(x1,x2), ylim(y1,y2) o “okrągłych” granicach spowoduje, że odpowiedni podział pola graficznego będzie zgadzał się z pożądanym wyglądem siatki.
Można to zobaczyć za pomocą programu:
windows(4.5, 2.5)
par(mar=c(2,2,1,1), xaxs="i", yaxs="i")
plot(c(4,2,3,5,1,2), xlim=c(0,7), ylim=c(0,6))
grid(nx=7, ny=6, col="#ccffff", lty=1, lwd=2)
points(1:6,c(4,2,3,5,1,2))
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1))
barplot(c(4,2,3,5,1,2))
grid(nx=NA, ny=NULL, col="#ffccff", lty=1, lwd=2)
barplot(c(4,2,3,5,1,2),add=TRUE)
#
windows(4.5, 2.5)
par(mar=c(1,2,1,1), yaxs="i")
boxplot(1:6, axes=FALSE)
axis(2,at=10:60/10, labels=rep("",51), tck=-0.02)
grid(nx=NA, ny=50, col="#ccffcc", lty=1, lwd=2)
axis(2,at=2:12/2, labels=rep("",11), tck=-0.04)
grid(nx=NA, ny=10, col="#99ff99", lty=1, lwd=2)
axis(2,at=1:6)
grid(nx=NA, ny=NULL, col="#55ff55", lty=1, lwd=2)
boxplot(1:6, axes=FALSE, col="white", add=TRUE)
|
Program tworzy następujące wykresy:
Ostatni z przykładów pokazuje, że przy tworzeniu właściwej siatki najlepiej posługiwać się wszystkimi trzema sposobami.
Czcionlka, napisy, podpisy, tytuł
Wielkość i rodzaj czcionki
Rozmiar czcionki ustala się opcją ps=n w funkcji par(). Domyślnie jest to 12 jednostek, a jednostka to 1/72 cala. Zastosowanie w tej opcji określa rozmiar wszystkich symboli tekstowych (liter i liczb), a więc etykiet, podpisów osi i innych elementów tekstowych. W funkcjach graficznych istnieją opcje, takie jak:
- cex.axis=x zmieniające wielkość czcionki w etykietach,
- cex.lab=x zmieniające wielkość czcionki w podpisach osi,
- cex.main=x zmieniająca wielkość czcionki w tytule wykresu,
- cex.sub=x zmieniająca wielkość czcionki w podpisie wykresu,
które zwiększają lub zmniejszają x – razy czcionkę ustaloną opcją ps=n. Liczba x przyjmuje zatem najczęściej wartości od 0.5 do 1.5, choć może być dowolną liczbą dodatnią. Ustalanie wielkości czcionek pokazuje następujący program:
windows(4.5, 2.5)
par(mar=c(4, 3, 2, 1), mgp=c(1.7, 0.5, 0), tck=-0.03, ps=10)
plot(5:15, type="n", xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="Tytuł",
sub="Podpis", cex.axis=1.2, cex.lab=0.8, cex.main=1.1, cex.sub=1.3)
#
windows(4.5, 2.5)
par(mar=c(4, 3, 2, 1), mgp=c(1.7, 0.5, 0), tck=-0.03, ps=12)
plot(5:15, type="n", xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="Tytuł",
sub="Podpis", cex.axis=0.8, cex.lab=1.2, cex.main=1.3, cex.sub=1.1)
|
Po wykonaniu programu pokazują się dwa wykresy:
W funkcji text() rozmiar czcionek ustala się za pomocą parametru cex=x, gdzie x=1 odpowiada domyślnej wielkości czcionki odczytanej z funkcji par(). Inne wielkości cex=x odpowiednio ją zwiększają lub zmniejszają. Można przetestować wymiary czcionek za pomocą programu:
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(5:15, type="n", axes=FALSE, xlab="", ylab="")
for (i in 5:20) {text(3,i, "Ala ma kota", cex=i/10, adj=0)
text(9,i,paste("cex =",i/10), cex=1, adj=0)}
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(5:15, type="n", axes=FALSE, xlab="", ylab="")
for (i in 5:20) {par(ps=i)
text(3,i, "Ala ma kota", adj=0)
par(ps=12)
text(9,i, paste("ps =",i), adj=0)}
|
Wygenerowane wykresy wyglądają następująco:
Ponadto każdy tekst można napisać czcionka pogrubioną lub kursywą (italikiem) oraz pogrubioną kursywą. Służą do tego opcje:
- font.axis=n określająca rodzaj czcionki w etykietach,
- font.lab=n określająca rodzaj czcionki w podpisach osi,
- font.main=n określająca rodzaj czcionki w tytule,
- font.sub=n określająca rodzaj czcionki w podpisie wykresu.
Liczba n może mieć wartości 1, 2, 3 i 4, gdzie:
- 1 oznacza normalne pismo
- 2 oznacza pismo pogrubione
- 3 oznacza kursywę (pismo pochyłe)
- 4 oznacza pismo pochyłe i pogrubione
Odpowiednikiem tej opcji w funkcji text() jest font=n. Działanie tych opcji wygląda następująco:
windows(4.5, 2.5)
par(mar=c(4, 3, 2, 1), mgp=c(1.7, 0.5, 0), tck=-0.03 )
plot(5:15, type="n", xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="Tytuł",
sub="Podpis", font.axis=1, font.lab=2, font.main=3, font.sub=4)
for (i in 1:4) {text(4,(5-i)*2, "Ala ma kota", adj=0, font=i)
text(8,(5-i)*2, paste("font =",i), adj=0)}
#
windows(4.5, 2.5)
par(mar=c(4, 3, 2, 1), mgp=c(1.7, 0.5, 0), tck=-0.03)
plot(5:15, type="n", xlab="Podpis osi 0X", ylab="Podpis osi 0Y", main="Tytuł",
sub="Podpis", font.axis=3, font.lab=4, font.main=1, font.sub=2)
for (i in 1:4) {text(4,(5-i)*2, "Ala ma kota", adj=0, font=i)
text(8,(5-i)*2, paste("font =",i), adj=0)}
|
Wykresy powstające, jako wynik uruchomienia tego programu wyglądają następująco:
Krój czcionki
Zmiana kroju czcionki na wykresach w R sprawia dość dużo problemów, bo nie ma na to prostej opcji w funkcjach graficznych. Standardowo przyjętym krojem jest “Arial Unicode” zdefiniowany dla różnych systemów podobnie. Tymczasem R umożliwia posługiwanie się każdą czcionką jaką dysponuje system operacyjny. Wystarczy znaleźć tylko nazwę systemową tej czcionki, a R ją użyje.
W systemie Windows 10 znalezienie nazw krojów czcionek polega na:
- kliknięciu na ikonkę “Okna” w lewym dolnym rogu pulpitu (tą, która uruchamia podgląd wszystkich programów i wyróżnione kafle),
- kliknięciu na ikonkę “Ustawienia” (będącą zazwyczaj powyżej ikonki “Zasilanie”),
- wpisaniu w górne pole z napisem “Znajdź ustawienie” słowa “czcionka”,
- wybraniu pokazującej się opcji “Ustawienia czcionek” i kliknięciu na nią.
Pojawi się obszerne pole z zainstalowanymi krojami czcionek, przykładowym napisem wykonanym tym krojem. Dodatkowo, gdy napis ten wykonany jest po polsku to możemy być pewni, że ten krój zawiera polskie litery. Ich nazwy zapisane są pod spodem, a dodatkowe informacje pokazują, czy dany krój ma swój odpowiednik w kursywie lub czcionkach pogrubionych.
Po wybraniu krojów, trzeba im przypisać w R odpowiedni literał i wykonać funkcję windowsFonts(). Można jednorazowo przypisać nazwy kilku czcionek systemowych z nazwami, których będzie się używało w R i funkcję tę uruchamiać, kiedy tylko zajdzie potrzeba zmiany czcionki w wykresach. Przykładowo, funkcja ta napisana dla systemu Windows 10 została podana w pierwszej części poniższego programu. W drugiej części pokazano jak wykożystać zaimplementowane czcionki do wykonania napisy “Źrebak złamał kość”.
windowsFonts(Arial = windowsFont("Arial"),
Cambria = windowsFont("Cambria"),
Comic = windowsFont("Comic Sans MS"),
Consolas = windowsFont("Consolas"),
Constantia = windowsFont("Constantia"),
Corbel = windowsFont("Corbel"),
Courier = windowsFont("Courier New"),
Georgia = windowsFont("Georgia"),
Impact = windowsFont("Impact"),
Palatino = windowsFont("Palatino Linotype"),
Symbol = windowsFont("Symbol"))
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:10, type="n", axes=FALSE, xlab="", ylab="")
par(family="Cambria")
text(1,10, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,10, "Cambria", adj=0)
par(family="Comic")
text(1,9, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,9, "Comic", adj=0)
par(family="Consolas")
text(1,8, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,8, "Consolas", adj=0)
par(family="Constantia")
text(1,7, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,7, "Constantia", adj=0)
par(family="Corbel")
text(1,6, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,6, "Corbel", adj=0)
par(family="Georgia")
text(1,5, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,5, "Georgia", adj=0)
par(family="Impact")
text(1,4, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,4, "Impact", adj=0)
par(family="Palatino")
text(1,3, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,3, "Palatino", adj=0)
par(family="Symbol")
text(1,2, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(6,2, "Symbol", adj=0)
|
Program spowodował powstanie następującego wykresu:
Po wykonaniu funkcji windowsFonts() możemy posługiwać się skróconymi nazwami krojów czcionek w opcji family=”nazwa kroju czcionki” funkcji par(). Krój ten może ulegać pogrubieniu lub kursywie poprzed dodanie opcji font.
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:10, type="n", axes=FALSE, xlab="", ylab="")
par(family="Cambria")
text(1,10, "Ala ma kota", adj=0)
par(family="Arial")
text(6,10, "Cambria", adj=0)
par(family="Comic")
text(1,9, "Ala ma kota", adj=0)
par(family="Arial")
text(6,9, "Comic", adj=0)
par(family="Consolas")
text(1,8, "Ala ma kota", adj=0)
par(family="Arial")
text(6,8, "Consolas", adj=0)
par(family="Constantia")
text(1,7, "Ala ma kota", adj=0)
par(family="Arial")
text(6,7, "Constantia", adj=0)
par(family="Corbel")
text(1,6, "Ala ma kota", adj=0)
par(family="Arial")
text(6,6, "Corbel", adj=0)
par(family="Pristina")
text(1,5, "Ala ma kota", adj=0)
par(family="Arial")
text(6,5, "Pristina", adj=0)
par(family="Georgia")
text(1,4, "Ala ma kota", adj=0)
par(family="Arial")
text(6,4, "Georgia", adj=0)
par(family="Impact")
text(1,3, "Ala ma kota", adj=0)
par(family="Arial")
text(6,3, "Impact", adj=0)
par(family="Ravie")
text(1,2, "Ala ma kota", adj=0)
par(family="Arial")
text(6,2, "Ravie", adj=0)
par(family="Palatino")
text(1,1, "Ala ma kota", adj=0)
par(family="Arial")
text(6,1, "Palatino", adj=0)
|
Program generuje jeden wykres, ale poprzez dodanie opcji font=2 i font=3 do funkcji text() z tekstem “Ala ma kota” tworzą się pozostałe dwa wykresy.
Pod pewnymi krojami czcionek nie kryją się litery i cyfry, ale inne symbole. Mogą one mieć znaczenie na niektórych wykresach i zamiast je rysować można użyć gotowych znaków. Do takich czcionek należy “Symbol”, “Webdings” i “Wingdings”. Można zobaczyć, co kryje się w tych krojach pod znakami, które możemy wprowadzić z klawiatury. Dla czcionki “Symbol” można wykonać program:
windows(4.5, 2.5)
par(mar=c(1,1,1,1))
plot(1:10, type="n", axes=FALSE, xlab="", ylab="", xlim=c(1,11))
for (j in 1:3){
for (i in ((j-1)*10+1):(j*10)){
par(family="Symbol")
text(j,j*10+1-i, letters[i], adj=0)
par(family="TimesNewRoman")
text(j+0.3,j*10+1-i, letters[i], adj=0, col=grey(0.5))}}
for (j in 1:3){
for (i in ((j-1)*10+1):(j*10)){
par(family="Symbol")
text(j+3,j*10+1-i, LETTERS[i], adj=0)
par(family="TimesNewRoman")
text(j+3+0.3,j*10+1-i, LETTERS[i], adj=0, col=grey(0.5))}}
for (i in 1:10) {
par(family="Symbol")
text(7,11-i, paste(0:9)[i], adj=0)
par(family="TimesNewRoman")
text(7.3,11-i, paste(0:9)[i], adj=0, col=grey(0.5))}
znaki1=c("~", "`", "!", "@", "#", "$", "%", "^", "&", "*")
znaki2=c("(", ")", "_", "-", "+", "=", "|", "{", "[", "}")
znaki3=c("]", ":", ";", ",", "<", ">", ".", "?", "/")
for (i in 1:10) {
par(family="Symbol")
text(8,11-i, znaki1[i], adj=0)
par(family="TimesNewRoman")
text(8.3,11-i, znaki1[i], adj=0, col=grey(0.5))}
for (i in 1:10) {
par(family="Symbol")
text(9,11-i, znaki2[i], adj=0)
par(family="TimesNewRoman")
text(9.3,11-i, znaki2[i], adj=0, col=grey(0.5))}
for (i in 1:10) {
par(family="Symbol")
text(10,11-i, znaki3[i], adj=0)
par(family="TimesNewRoman")
text(10.3,11-i, znaki3[i], adj=0, col=grey(0.5))}
|
Uzyskany wykres pokaże na czarno znaki, jakie kryją się pod znakami z klawiatury zaznaczonymi na szaro. Po zmianie słowa “Symbol” na “Webdings” oraz na “Wingdings” uzyskamy drugi i trzeci wykres.
Ważne są litery greckie w czcionkach “Symbol”, gdyż często występują one w jednostkach zmiennych. Jednak ich pisanie razem z innym krojem czcionek jest kłopotliwe. Są na to inne sposoby wyjaśnione w następnym podrozdziale.
Znaki specjalne, symbole matematyczne
W podpisach osi często trzeba użyć jednostek pomiaru zmiennych ciągłych z indeksami górnymi lub dolnymi i greckimi literami. Taki podpis programuje się za pomocą funkcji expression(), która wystąpiwszy w funkcjach graficznych przetwarza wyrażenie tekstowe o specjalnej składni na odpowiednio wyglądający tekst. Chodzi tu przede wszystkim o wyrażenia matematyczne, które w funkcji expression() zapisuje się za pomocą znaków dostępnych na klawiaturze, a ogląda na wykresach w taki sposób, w jaki przywykliśmy na lekcjach matematyki. Żeby to zrozumieć, trzeba to zobaczyć na przykładzie.
Przypuśćmy, że w podpisach pod osiami musimy napisać jednostki, w jakich mierzone były objętości jąder komórkowych i są to ηm3 lub stężenie ołowiu w μg/g lub μg·g-1. W wielu językach programistycznych można napisać litery greckie i używać indeksów górnych, ale w konsoli R nie jest to możliwe. Trzeba użyć specjalnej notacji, którą zrozumie funkcja expression() i przetworzy na odpowiednio wyglądający tekst. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3.6,3.6,1,1),mgp=c(1.7,0.5,0), tck=-0.03)
plot(1:2,type="n",
xlab=expression("objętość jądra komórkowego [" * eta * m^3 * " ]"),
ylab=expression("stężenie Pb [ " * mu * g %.% g^-1 * "]"))
|
Wykonanie powyższego programu spowoduje powstanie następującego wykresu:
Funkcja expression(napis) zastępuje napis w odpowiedni tekst. Elementy składające się na napis łączone są znakiem *. Wygląda to następująco:
expression( czlon1 * czlon2 * … * czlon k)Poszczególne człony, rozdzielone znakiem *, nie przecinkami, będą osobno przetwarzane i wyniki zostaną napisane jeden za drugim. Członami mogą być dowolne zestawienia liter, które zostaną nie zmienione o ile nie oznaczają jakiejś greckiej litery lub są nazwą funkcji rozumianej przez expression(). Spacje i teksty zapisane w cudzysłowie ” ” nie będą zmieniane. Natomiast specjalne zestawy znaków (liter i znaków znajdujących się na klawiaturze) oraz specjalne funkcje wewnętrzne funkcji expression() w zdefiniowany sposób zamieniają na znaki specjalne i konstrukcje matematyczne. Wykaz takich typowych konstrukcji znajduje się w helpie R. Znajdziemy go wpisując w konsoli ?plotmath. Tu podamy tylko podstawowe informacje.
Funkcja expression() przekształca następujące zestawy liter łacińskich na litery greckie:
|
Wynik działania
funkcji expression() |
|
| alpha | α | |
| beta | β | |
| gamma | γ | |
| delta | δ | |
| epsilon | ε | |
| zeta | ζ | |
| eta | η | |
| theta | θ | |
| iota | ι | |
| kappa | κ | |
| lambda | λ | |
| mu | μ | |
| nu | ν | |
| xi | ξ | |
| omicron | ο | |
| pi | π | |
| rho | ρ | |
| sigma | σ | |
| tau | τ | |
| upsilon | υ | |
| phi | φ | |
| chi | χ | |
| psi | ψ | |
| omega | ω |
| Zestaw liter łacińskich |
Wynik działania
funkcji expression()
AlphaΑBetaΒGammaΓDeltaΔEpsilonΕZetaΖEtaΗThetaΘIotaΙKappaΚLambdaΛMuΜNuΝXiΞOmicronΟPiΠRhoΡSigmaΣTauΤUpsilonΥPhiΦChiΧPsiΨOmegaΩ
Indeks dolny uzyskamy pisząc expression(x[i]), a indeks górny (potęgę) uzyskamy pisząc expression(x^i). Zamiast pojedynczego symbolu w miejsce “i” można wpisać dowolnie długi tekst pod warunkiem, że nie ma w nim liczb, pauzy, przecinka i innych znaków przystankowych. Litery z liczbami muszą być objęte funkcją paste(). Ponieważ często trzeba tych znaków użyć w końcowym tekście, pożądany efekt uzyskuje się pisząc “~” w miejsce pauzy i spinając symbole rozdzielone przecinkami funkcją list().
windows(4.5, 2.5)
par(mar=c(1,1,1,1),mgp=c(1.7,0.5,0), tck=-0.03)
plot(1:10,type="n", xlab="", ylab="", axes=FALSE)
text(3, 4, expression(x[i]*", "*x[i+1]*", "*x[indeksy~dolne]*",
"*x[list(i,j,k)]), cex=1.4, adj=0)
text(3, 7, expression(x^i*", "*x^list(i+1)*", "*x^list(indeksy~górne)*",
"*x^list(i,j,k)), cex=1.4, adj=0)
|
W efekcie uzyskujemy wykres postaci:
Funkcja expression(sqrt(x)) pozwala zapisać x pod pierwiastkiem, a expression(sqrt(1-x^2)) daje poprawny wzór matematyczny (pierwiastek z 1 – x do kwadratu). Często poszukiwany daszek nad x (lub innym wyrażeniem) uzyskamy stosując funkcje hat(x) lub widehat(x). Natomiast kreskę nad x stosowaną na oznaczenie średniej uzyskamy pisząc bar(x). Dla bardziej złożonych wzorów często znajdziemy podpowiedź w Internecie, gdyż jest to popularny temat wśród matematyków.
windows(4.5, 2.5)
par(mar=c(1,1,1,1),mgp=c(1.7,0.5,0), tck=-0.03)
plot(1:10,type="n", xlab="", ylab="", axes=FALSE)
text(3, 7, expression(bar(x)*" = "*frac(1, n)*sum(x[i], i==1, n)),
cex=1.4, adj=0)
text(5, 4, expression(paste(frac(1, sigma*sqrt(2*pi))*" "*
plain(e)^{frac(-(x-mu)^2, 2*sigma^2)})), cex=1.4, adj=0)
|
Rezultatem działania programu jest wykres:
Biologów jednak bardziej zainteresuje fakt, że funkcja expression() pozwala także pogrubiać i pochylać wybrane fragmenty w napisach i podpisach. Służą do tego funkcje bold(), italic(), bolditalic(), którymi należy objąć pewne partie tekstu. Można też fragment tekstu podkreślić obejmując go funkcją underline(), napisać z szerszymi odstępami między literami obejmując go funkcją displaystyle(), zmniejszyć tekst obejmując go funkcja scriptstyle() lub scripscriptstyle(). Daje to dodatkowe efekty w podpisach osi, tytułach i podpisach.
windows(4.5, 2.5)
par(mar=c(4, 3, 2, 1), mgp=c(1.7, 0.5, 0), tck=-0.03, ps=14)
plot(5:15, type="n", xlab=expression(underline(Podpis)*" osi 0X"),
ylab=expression("Podpis " * bolditalic(osi)*" "*bold(paste(0,Y))),
main=expression("Tytuł "*scriptstyle(Tytuł)*" "*scriptscriptstyle(Tytuł)))
|
Wstawienie powyższego kodu do konsoli powoduje powstanie następującego wykresu:
Zestawienie wszystkich możliwych efektów powoduje, że możemy stosunkowo swobodnie komponować wykresy w R, zwłaszcza gdy chodzi o rodzaje tekstów wstawianych do wykresu.
Umiejscowienie i obracanie napisów
Temat umiejscowienia napisów, podpisów i tytułu na wykresie pojawiał się już wcześniej, gdyż bez tego nie dałoby się pokazać przykładów użycia różnych opcji graficznych. W szczególności stosowano już kilka razy podrzędną funkcję graficzną text() służącą głównie do wstawiania tekstu w obrębie pola kreślenia. Jej obowiązkowymi argumentami są współrzędne punktu wskazującego gdzie ma pojawić tekst. W rozdziale o osiach wykresu omówiono opcję adj=x, która ustalała różne wyrównanie podpisów osi (do lewej, wyśrodkowanie, do prawej lub do dołu, wyśrodkowanie do góry) gdy x przyjmowało wartości 0, 0.5 i 1. Opcja ta w funkcji text() pokazuje, jak pisany jest tekst względem współrzędnych punktu , które należy podać na dwóch pierwszych miejscach. Funkcja ta ma jeszcze jedną opcję wyrównującą tekst: pos=n, gdzie n jest liczba od 1 do 4. Domyślnie ma wartość NULL, ale gdy zostanie jej przyporządkowana jakaś wartość liczbowa, to opcja adj zostanie pominięta. Poszczególne wartości opcji pos=n działają następująco:
- pos=1 Tekst znajdzie się powyżej podanego punktu współrzędnych wyśrodkowany.
- pos=2 Tekst znajdzie się na lewo od podanego punktu współrzędnych wyrównany do prawej.
- pos=3 Tekst znajdzie sie na prawo od podanego punktu współrzędnych wyrównany do lewej.
- pos=4 Tekst znajdzie się poniżej podanego punktu współrzędnych wyśrodkowany
Działanie obu opcji adj=x i pos=n w funkcji text() zobaczyć można za pomocą programu:
windows(4.5, 2.5)
par(mar=c(1,1,2,1), mgp=c(2,1,0))
plot(1:3, type="n", xlab="", ylab="", axes=FALSE, main="pos=NULL")
points(2,1.5, col="green", pch=20)
text(2,1.5, "Ala ma kota \n(adj=1)", adj=1)
points(1.5,2, col="blue", pch=20)
text(1.5,2, "Ala ma kota \n(adj=0.75)", adj=0.75)
points(2,2.5, col="red", pch=20)
text(2,2.5, "Ala ma kota \n(adj=0)", adj=0)
points(2.5,2, col="magenta", pch=20)
text(2.5,2, "Ala ma kota \n(adj=0.25)", adj=0.25)
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), mgp=c(2,1,0))
plot(1:3, type="n", xlab="", ylab="", axes=FALSE, main="adj dowolne")
points(2,1.5, col="green", pch=20)
text(2,1.5, "Ala ma kota \n(pos=1)", pos=1)
points(1.5,2, col="blue", pch=20)
text(1.5,2, "Ala ma kota \n(pos=2)", pos=2)
points(2,2.5, col="red", pch=20)
text(2,2.5, "Ala ma kota \n(pos=3)", pos=3)
points(2.5,2, col="magenta", pch=20)
text(2.5,2, "Ala ma kota \n(pos=4)", pos=4)
|
Program generuje dwa wykresy:
Do obrotu tekstu (ale tylko tekstu napisanego funkcją text()) służy opcja srt=x, gdzie x jest liczba rzeczywistą oznaczającą kąt zapisany w stopniach. Obrót o kąt dodatni następuje zgodnie z ruchem przeciwnym do ruchu wskazówek zegara. Obrót zachodzi względem punktu o podanych współrzędnych. Odgrywają w nim zatem sposoby wyrównania tekstu względem tego punktu. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(1,1,2,1), mgp=c(2,1,0))
plot(1:3, type="n", xlab="", ylab="", axes=FALSE, main="pos=NULL, srt=30")
points(2,1.5, col="green", pch=20)
text(2,1.5, "Ala ma kota \n(adj=1)", adj=1, srt=30)
points(1.5,2, col="blue", pch=20)
text(1.5,2, "Ala ma kota \n(adj=0.75)", adj=0.75, srt=30)
points(2,2.5, col="red", pch=20)
text(2,2.5, "Ala ma kota \n(adj=0)", adj=0, srt=30)
points(2.5,2, col="magenta", pch=20)
text(2.5,2, "Ala ma kota \n(adj=0.25)", adj=0.25, srt=30)
#
windows(4.5, 2.5)
par(mar=c(1,1,2,1), mgp=c(2,1,0))
plot(1:3, type="n", xlab="", ylab="", axes=FALSE, main="adj dowolne, srt=30")
points(2,1.5, col="green", pch=20)
text(2,1.5, "Ala ma kota \n(pos=1)", pos=1, srt=30)
points(1.5,2, col="blue", pch=20)
text(1.5,2, "Ala ma kota \n(pos=2)", pos=2, srt=30)
points(2,2.5, col="red", pch=20)
text(2,2.5, "Ala ma kota \n(pos=3)", pos=3, srt=30)
points(2.5,2, col="magenta", pch=20)
text(2.5,2, "Ala ma kota \n(pos=4)", pos=4, srt=30)
|
Program tworzy dwa wykresy wyglądające następująco:
Stosunkowo najlepiej obraca się tekst względem punktu znajdującego się w jego środku, czyli dla parametrów domyślnych wartości opcji adj=0.5 i pos=NULL. Najczęściej potrzebny jest obrót taki, by uzyskać tekst pionowy. Współrzędne punktu tekstu docelowego ustalamy tak, by wypadły w środku tekstu. Dla osi lewej pasuje obrót o 90°, dla osi prawej o 270°. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,1,3), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X", ylab="Podpis osi 0X",main="")
axis(4,at=1:5*2)
mtext("Podpis drugiej osi 0Y", 4, 1.7)
text(1,5.5,"Tu są wartości zmiennej Y", srt=90, cex=0.8)
text(10,5.5,"Tu są wartości zmiennej Z", srt=270, cex=0.8)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,3), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X", ylab="Podpis osi 0X",main="", las=1)
axis(4,at=1:5*2, las=1)
par(xpd=TRUE)
text(11.7,5.5,"Podpis drugiej osi 0Y", srt=270)
text(1,5.5,"Tu są wartości zmiennej Y", srt=90, cex=0.8)
text(10,5.5,"Tu są wartości zmiennej Z", srt=270, cex=0.8)
|
Dzięki temu programowi powstają dwa następujące wykresy:
W nadrzędnych funkcjach graficznych, mtext(), axis() i wszystkich innych niż text() nie możemy obracać tekstu.
Umieszczanie napisów na marginesach
Na marginesach pojawiają się standardowo podpisy osi, które można napisać za pomocą opcji xlab=”” i ylab=”” wszystkich nadrzędnych funkcji graficznych. We wszystkich tych funkcjach opcja main=”” wstawia tytuł na marginesie górnym, a opcja sub=”” wstawia podpis na marginesie dolnym. Umiejscowienie podpisów osi określa opcja mgp=c(z,y,x), którą najczęściej umieszcza się w funkcji par() poprzedzającej funkcje graficzna rysującą lub w funkcjach axis(). Liczby x, y i z liczy się w jednostkach zwanych linijkami wynoszącymi 0.2 cala i określonymi jako odległość od brzegu pola kreślenia. Liczba x określa płożenie osi względem brzegu pola kreślenia i najczęściej ma wartość 0. Liczba y określa miejsce pisania etykiet i jej domyślna wartość (y=1) jest na małych wykresach zazwyczaj zbyt duża. Liczba z określa linijkę, w której umieszczany jest podpis osi (domyślnie 3). Wielkości te mogą być liczbami rzeczywistymi i można im nadać dowolna wartość, nawet ujemną. Trzeba pamiętać, że opcja mgp=c(x,y,z) w funkcji par() lub nadrzędnej funkcji graficznej działa jednakowo na wszystkie osie. Tytuł domyślnie wstawia się w środek marginesu górnego, a podpis wykresu linijkę za podpisem dolnej osi. Wygląda to następująco:
windows(4.5, 2.5)
plot(1:10, type="n",xlab="Podpis osi 0X", ylab="Podpis osi 0Y",main="Tytuł",
sub="Podpis")
#
windows(4.5, 2.5)
par(mar=c(4,3,2,1), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X", ylab="Podpis osi 0Y",main="Tytuł",
sub="Podpis", font.main=1)
|
Powstają dwa wykresy:
Po zastosowaniu opcji mar=c(x1,x2,x3,x4) i mgp=c(x,y,z) zazwyczaj otrzymujemy zadowalający wykres. Problemy pojawiają się wtedy, gdy umieszczenie podpisów pod osią 0X jest kilkulinijkowy. Nie wystarcza bowiem zwiększenie marginesu dolnego, ale trzeba też odsunąć podpis osi od etykiet. Ciekawe, że kilkulinijkowy podpis osi 0Y nie wymaga takich poprawek. Widać to po wykonaniu następującego programu:
windows(4.5, 2.5)
par(mar=c(5,3.5,2,1), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X \nzajmuje dwie linijki",
ylab="Podpis osi 0Y", main="Tytuł", sub="Podpis", font.main=1)
#
windows(4.5, 2.5)
par(mar=c(5,3.5,2,1), mgp=c(2.5,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X \nzajmuje dwie linijki",
ylab="Podpis osi 0Y", main="Tytuł", sub="Podpis", font.main=1)
#
windows(4.5, 2.5)
par(mar=c(4,4,2,1), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X",
ylab="Podpis osi 0Y \nzajmuje dwie linijki",
main="Tytuł", sub="Podpis", font.main=1)
|
Program generuje trzy wykresy:
W przypadku wielolinijkowego podpisu osi 0X możemy mieś albo nadpisane etykiety dolnej osi albo za bardzo wysunięty w lewo podpis osi 0Y. W tym wypadku, podpis osi 0Y należy wstawić funkcją mtext(), a w nadrzędnej funkcji graficznej wstawić ylab=””.
Choć funkcja mtext() różni się tylko jedną literą od funkcji text() jej konstrukcja jest inna. Jej pierwszym obowiązkowym argumentem jest tekst, który ma być napisany na wykresie, ujęty w cudzysłów (albo napisany funkcją expression()), drugim jest numer marginesu, trzecim linijka, w której ma być napisany text. Trzeci argument może być dowolną liczba rzeczywistą.
windows(4.5, 2.5)
par(mar=c(5,3,2,1), mgp=c(2.5,0.5,0))
plot(1:10, type="n",xlab="Podpis osi 0X \nzajmuje dwie linijki",
ylab="", main="Tytuł", sub="Podpis", font.main=1)
mtext("Podpis osi 0Y",2,1.7)
|
Powstanie w ten sposób następujący wykres:
Funkcja mtext() umożliwia także podpisywanie osi dodatkowej 0Y wstawianej na czwartym marginesie i wstawianie wszelkich dodatków tekstowych na marginesach górnym i dolnym. Opcja adj=0.5 na każdym marginesie wyśrodkowuje tekst (jest to wartość domyślna, ale można go wyrównać do lewej lub w dół pisząc adj=0 lub do prawej / w górę pisząc adj=1. Może też przyjmować wartości ujemne lub większe od 1, co umożliwia pisanie w rogach wykresu. Zazwyczaj w lewym górnym rogu wpisywane są oznaczenia wykresów, gdy na jednej rycinie jest ich kilka. Zazwyczaj są to litery “A”, “B”,… i gdy rycina ma podpis zaczynający się od Ryc.2., to powołujemy się na poszczególne wykresy (ryc.2.A, ryc.2.B) itd. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,2,1), mgp=c(1.7,0.5,0))
plot(1:10, type="n",xlab="Odległość od portu w Gdynii [km]",
ylab="Stężenie PCBs [mg/kg]", main="Zatoka Pucka", font.main=1)
mtext("A",3,1,adj=-0.15, xpd=NA, font=2)
#
windows(4.5, 2.5)
par(mar=c(3,3,2,1), mgp=c(1.7,0.5,0))
plot(1:20, type="n",xlab="Odległość od portu w Świnoujściu",
ylab="Stężenie PCBs [kg/g]", main="Okolice Świnoujścia", font.main=1)
mtext("B",3,1,adj=-0.15, xpd=NA, font=2)
|
Program generuje dwa wykresy:
Napisy na marginesach można dodać stosując funkcję graficzną dokładającą title(). Jej opcjami są właśnie main, sub, xlab, ylab (w tej właśnie kolejności), numer linijki, w której ma się wpisać tekst, oraz wszystkie opcje graficzne, które przetwarzają tekst. Zazwyczaj stosuje się ją dla tytułu lub podpisu wykresu, umieszczając go w odpowiednim miejscu na marginesie górnym (main=””) lub dolnym (sub=””).
Poniższy program pokazuje standardowe użycie funkcji title().
windows(4.5, 2.5)
par(mar=c(3,3,2,1), mgp=c(1.7,0.5,0))
plot(1:100, type="n",xlab="Podpis osi 0X", ylab="Podpis osi oY", main="")
title("Tytuł wykresu")
#
windows(4.5, 2.5)
par(mar=c(4,3,1,1), mgp=c(1.7,0.5,0))
plot(1:100, type="n",xlab="Podpis osi 0X", ylab="Podpis osi oY", main="")
title(sub="Podpis wykresu")
|
Powoduje on powstanie dwóch wykresów.
Powstałe wykresy są takie same jak umieszczenie odpowiednich tekstów w opcjach main=”” i sub=”” odpowiednich funkcji graficznych. Funkcja title() ma także opcję outer=TRUE, która umożliwia zrobienie wspólnego tytułu dla kilku wykresów umieszczonych na jednej rycinie, a także stosowanie wspólnych podpisów osi, gdy brzmią one identycznie na kilku wykresach.
windows(9, 5)
layout(matrix(1:4,2,2,byrow=TRUE))
layout.show(4)
#
par(mar=c(1,1,1,1), oma=c(3,3,2,0), mgp=c(1.7,0.5,0))
plot(1:100, type="n", xlab="", ylab="", main="")
plot(1:100, type="n", xlab="", ylab="", main="")
plot(1:100, type="n", xlab="", ylab="", main="")
plot(1:100, type="n", xlab="", ylab="", main="")
#
title("Wspólny tytuł wykresu", outer=TRUE)
title(xlab="Wspólny podpis osi 0X",outer=TRUE, cex.lab=1.2, font.lab=2)
title(ylab="Wspólny podpis osi 0Y",outer=TRUE, cex.lab=1.2, font.lab=2)
|
Powyższy program powoduje powstanie wykresu:
Tego typu złożone ryciny mają wystarczające minimum potrzebnych wyjaśnień i eksponują przede wszystkim dane.
Legenda
Elementy tworzące legendę
Legenda jest obowiązkowym obiektem na złożonych wykresach robionych w biologii, na których trzeba wyjaśnić znaczenie wszystkich użytych kolorów, stylów linii, rodzajów znaczników i innych symboli. Polega ona na umieszczeniu gdzieś na wykresie tabelki złożonej z dwóch kolumn. Na lewo są symbole, lub małe odcinki linii o określonych stylach i kolorach lub prostokąciki wypełnione określonym wzorem i kolorem. Na prawo są wyjaśnienia w formie słownej.
Żaden wykres w R nie ma domyślnej opcji pozwalającej na umieszczenie legendy na wykresie. Trzeba ja zrobić za pomocą podrzędnej funkcji graficznej legend(). Ma ona prawie 40 opcji, które umożliwiają zrobienie dobrej legendy we właściwym miejscu. Najważniejsze z nich można podzielić na kilka grup:
- Opcje x, y, xjust i yjus wskazujące na punkt, względem którego ma być umieszczona legenda.
- Opcje bty, bg, box.lty, box.lwd, box.col pokazujące jak ma wyglądać prostokąt okalający legendę.
- Opcje pch, col, lty, lwd, seg.len, fill, angle, density związane z punktami, liniami i prostokącikami z odpowiednimi kolorami umieszczane z lewej strony legendy.
- Opcja legend=c() pokazująca kolejne napisy ukazujące się z prawej strony legendy.
- Opcja title, title.col, title.adj pozwalające na zatytułowanie legendy.
Umiejscowienie legendy wynika z dwóch przesłanek:
- Legenda nie może przesłaniać informacji wynikającej z wykresu a więc żadnych punktów, linii i wzorów które umieszczono w polu kreślenia.
- Legenda nie może zabierać zbyt wiele miejsca, nie powinna generować zbyt wiele pustego miejsca i powinna tworzyć możliwie duże pole kreślenia.
Zatem legenda może być umieszczona wewnątrz pola kreślenia. Najczęściej jednak występuje na marginesach. Może też przecinać brzeg wykresu i tkwić częściowo w polu kreślenia i częściowo na marginesie. Wykonanie funkcji legend() poprzedza zazwyczaj wykonanie funkcji par(xpd=TRUE) co pozwala na rysowanie legendy lub jej elementów zarówno w polu kreślenia jak i na marginesie. Domyślna opcja xpd=FALSE powoduje, że legendę można utworzyć tylko w polu kreślenia, a to co wychodzi za to pole, znika.
Umiejscowienie legendy na przykładzie wykresów punktowych
Wykresy punktowe, w których zastosowano znaczniki o różnym kształcie lub kolorze wymagają legendy. Jej utworzenie wygląda następująco:
x.samice=c(0.32, 0.16, 0.34, 0.39, 1.55, 0.56, 0.13, 1.05, 0.15, 5.16, 4.41,
3.07, 4.72)
y.samice=c(7.34, 3.85, 5.27, 10.42, 2.16, 8.58, 9.51, 6.91, 5.05, 0.64, 1.92,
1.51, 2.65)
x.samce=c(0.07, 0.88, 5.14, 3.14, 1.50, 0.52, 0.48, 2.34, 1.98, 0.53, 0.63,
1.03, 0.69)
y.samce=c(9.72, 7.92, 0.15, 4.80, 5.88, 11.29, 9.40, 5.21, 3.98, 9.13, 9.08,
4.88, 5.40)
n1=length(x.samice)
n2=length(x.samce)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.04)
plot(c(x.samice,x.samce),c(y.samice,y.samce),
xlab="Odległość norki od szosy [m]",
ylab=expression("Stężenie ołowiu [ " * mu *"g/g]"),
pch=c(rep(15,n1),rep(17,n2)),
col=c(rep("green2",n1),rep("blue",n2)))
x0=par("usr")[2]
y0=par("usr")[4]
legend(x0,y0, xjust=1, yjust=1,
legend=c("samice","samce"),
pch=c(15,17),
col=c("green2","blue"))
|
Uzyskany wykres wygląda następująco:
Legenda umieszczana na polu kreślenia zazwyczaj zajmuje skrajną pozycję wolną od danych. Wtedy dobrze jest powołać się na współrzędne rogów pola kreślenia wyświetlanych przez funkcję par(“usr”) w kolejności współrzędne x1 i x2 dolnego brzegu i współrzędne y1 i y2 lewego brzegu. Opcje xjus=x i yjust=x pokazują jak ma być przesunięta legenda względem punktu (x,y) o współrzędnych podanych na początku. Ich wartości mogą być liczbą z przedziału [0,1] i w szczególności:
- xjus=0, yjust=0 oznacza, że legenda jest na prawo i powyżej punktu (x,y)
- xjust=0.5, yjust=0.5 oznacza, że punkt (x,y) jest w środku legendy
- xjust=1, yjust=1 oznacza, że legenda jest na lewo i poniżej punktu (x,y)
- xjust=0, yjust=1 (ustawienia domyślne) oznacza, że legenda jest na prawo i poniżej punktu (x,y)
Umiejscowienie legendy na marginesach wymaga zastosowania opcji xpd=TRUE (domyślnie ma wartość FALSE). Można to zrobić w opcji par() przed funkcją graficzną rysującą, w jej powtórzeniu przed funkcją legend() albo zastosować ją w funkcji legend(). Różne umiejscowienia legendy pokazują następujące programy:
windows(4.5, 2.5)
par(mar=c(3,3,1,6), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(par("usr")[2], par("usr")[4],
legend=c("czerwony", "niebieski"),
pch=c(3,5), col=c(2, 4))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,6), mgp=c(1.8,0.5,0))
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
par(xpd=TRUE)
legend(par("usr")[2], sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "niebieski"),
pch=c(3,5), col=c(2, 4))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,6), mgp=c(1.8,0.5,0))
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(par("usr")[2], par("usr")[3], xjust=0, yjust=0, xpd=TRUE,
legend=c("czerwony", "niebieski"),
pch=c(3,5), col=c(2, 4))
|
Po wykonaniu tego programu pojawiają się trzy wykresy, różniące się umiejscowieniem legendy na prawym marginesie, który musi być wcześniej zdefiniowany jako odpowiednio szeroki.
Aby zaoszczędzić nieco miejsca na pole kreślenia kosztem miejsca na legendę można wykonać następujący wykres:
windows(4.5, 2.5)
par(mar=c(3,3,1,3), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")legend(par("usr")[2]-1,
sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "niebieski"),
bg="white",
pch=c(3,5), col=c(2, 4))
|
Program generuje wykres:
Dość istotne jest w nim ustalenie koloru tła w prostokącie przeznaczonym na legendę opcją bg=”kolor”, bo domyślne ustawienie, to brak koloru tła. Wtedy brzeg wykresu byłby widoczny na legendzie.
Legendę można także umieścić na marginesie górnym albo dolnym, gdzie z reguły robi się to pod podpisem osi. Wymaga to napisania jej wierszy obok siebie. Służy do tego opcja horiz=TRUE. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,3,1), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(sum(par("usr")[1:2])/2, par("usr")[4]+0.5, xjust=0.5, yjust=0,
horiz=TRUE,
legend=c("czerwony", "niebieski"),
bg="white",
pch=c(3,5), col=c(2, 4))
#
windows(4.5, 2.5)
par(mar=c(5.5,3,1,1), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(c(1:6,1:6+0.5),c(6:1,1:6),
pch=c(3,3,3,5,5,5,3,3,3,5,5,5), col=c(2,2,2,4,4,4,2,2,2,4,4,4),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(sum(par("usr")[1:2])/2, par("usr")[3]-3, xjust=0.5, yjust=1,
horiz=TRUE,
legend=c("czerwony", "niebieski"),
bg="white",
pch=c(3,5), col=c(2, 4))
|
Program generuje następujące wykresy:
Legendę można też umiejscowić na lewym marginesie, choć jest to rzadko stosowane.
Wygląd i tytuł legendy na przykładzie wykresów liniowych
Wykresy liniowe wymagają legendy, jeśli widać na nich dwa lub więcej rodzajów linii. Często także tworzy się wykresy liniowo-punktowe, a to wymaga odpowiednio złożonej legendy. Wygląda to następująco:
y1=c(4,7,1,3,5,2)
y2=c(5,2,6,1,7,4)
y3=c(3,5,4,7,3,2)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,7), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(1:6,y1,type="l", lty=1, lwd=1, col="red", xlab="Podpis osi 0X",
ylab="Podpis osi 0Y")
lines(1:6,y2, lty=2, lwd=2, col="blue")
lines(1:6,y3, lty=3, lwd=2, col="green3")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "niebieski", "zielony"),
title="Legenda",
lty=c(1,2,3), lwd=c(1,2,2), col=c("red", "blue", "green3"))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,7.2), mgp=c(1.8,0.5,0), xpd=TRUE)
plot(1:6,y1,type="o", pch=15, lty=1, lwd=1, col="red",
xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
lines(1:6,y2, lty=2, lwd=2, col="blue")
points(1:6,y2, pch=17, col="blue")
lines(1:6,y3, lty=3, lwd=2, col="green3")
points(1:6,y3, pch=19, col="green3")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "niebieski", "zielony"),
title="Legenda",
pch=c(15,17,19), lty=c(1,2,3), lwd=c(1,2,2),
col=c("red", "blue", "green3"), seg.len=3)
|
Wykonanie powyższego programu w konsoli spowoduje powstanie następującego wykresu:
Na drugim wykresie wydłużono linie występujące w legendzie by były lepiej widoczne pod znacznikami. Zrobiono to opcją seg.len=x.
Legenda umiejscawiana na marginesie nie wymaga obramowania, albo przynajmniej obramowanie nie powinno być tak wyraźne jak obramowanie pola kreślenia. Zmienić to można opcja bty=””, która ma następujące wartości: “o” (domyślna) i “n” (oznacza brak obramowania). Przy opcji bty=”o” można zmienić rodzaj linii obramowania opcją box.lty=n, jej grubość opcją box.lwd=x i jej kolor opcja box.col. Jednocześnie można wprowadzić kolor tła legendy opcją bg=”color”. Opcje te nie działają, gdy bty=”n”.
Za pomocą poniższego programu można zmienić wygląd legendy.
windows(4.5, 2.5)
par(mar=c(3,3,1,6.7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:6,cbind(1:6,6:1), type="l", lty=2:3, lwd=2:3, col=2:3,
xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "zielony"),
title="Legenda",
box.lty=5, box.col=4, bg="#ccffff",
lty=c(2,3), col=2:3, lwd=2:3)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,6.7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:6,cbind(1:6,6:1), type="l", lty=2:3, lwd=2:3, col=2:3,
xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "zielony"),
title="Legenda",
box.lty=5, box.col=4, bg="#ccffff",
lty=c(2,3), col=2:3, lwd=2:3,
bty="n")
|
Program generuje następujące wykresy:
Dodanie opcji bty=”n” zlikwidowało działanie opcji związanych z wyglądem prostokąta na którym umieszczona jest legenda i wstawiło legendę bez obramowania.
Tytuł legendy nie zawsze jest potrzebny. Użycie haseł rozróżniających dane typu: “samiec”, “samica” nie wymaga wyjaśnienia, że jest to płeć. Ale już, na przykład, użycie wyjaśnień takich, jak “Negew”, “Lota” i “Registan”, wymagają tytułu “Pustynie”. Czasami jest to względne. W polskojęzycznej pracy nazwy “Wisła”, “Odra” nie wymagają tytułu, ale gdy przeznaczymy tę pracę do angielskojęzycznego czasopisma, lepiej jest zatytułować legendę “Rivers”.
Tytuł tworzy się przez dodanie opcji title=”” do funkcji legend() i powinien być najkrótszy jak się da. Często jest to słowo, które powinno być umieszczane przed każdym z haseł. Na przykład w tytule legendy jest “Ocean” a hasłami są “Atlanctycki”, “Spokojny”, “Indyjski”. Standardowo tytuł jest wyśrodkowany, ale można to zmienić opcją title.adj=x działającą tak, jak opcja adj=x w funkcji text(). Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,1,7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:6,cbind(1:6,6:1), type="l", lty=2:3, lwd=2:3, col=2:3,
xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "zielony"),
bty="n",
title="Legenda", title.adj=0,
lty=c(2,3), col=2:3, lwd=2:3)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:6,cbind(1:6,6:1), type="l", lty=2:3, lwd=2:3, col=2:3,
xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(6.3,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("czerwony", "zielony"),
bty="n",
title="Legenda", title.adj=0.85,
lty=c(2,3), col=2:3, lwd=2:3)
|
Program powoduje powstanie dwóch wykresów różniących się tylko umiejscowieniem tytułu legendy.
Napisy w legendzie można pogrubiać, pisać kursywą i stosować dla nich różne kolory. Służą do tego opcje text.font=n, text.col=”kolor”, title.col=”kolor”. Pogrybienie lub pochylenie czcionki tytułu legendy uzyskamy stosując opcje font w funkcji par() poprzedzającej legendę. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,1,5), mgp=c(1.8,0.5,0), xpd=TRUE, font=2)
matplot(1:5, outer(1:5,1:5), type="l", col=rainbow(5),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
text.font=1, text.col="blue", title.col="blue3",
bty="n", title="Tytuł",
legend=c(paste(letters[1:5],1:5)),
lty=1:5, col=rainbow(5))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,5), mgp=c(1.8,0.5,0), xpd=TRUE, font=3)
matplot(1:5, outer(1:5,1:5), type="l", col=rainbow(5),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
text.font=2, text.col="red", title.col="red3",
bty="n", title="Tytuł",
legend=c(paste(letters[1:5],1:5)),
lty=1:5, col=rainbow(5))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,5), mgp=c(1.8,0.5,0), xpd=TRUE, font=4)
matplot(1:5, outer(1:5,1:5), type="l", col=rainbow(5),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
text.font=3, text.col="green", title.col="green3",
bty="n", title="Tytuł",
legend=c(paste(letters[1:5],1:5)),
lty=1:5, col=rainbow(5))
|
Po wykonaniu tego programu powstają trzy wykresy:
Zdarza się, że w legendzie trzeba wyróżnić tak wiele wierszy, że się nie mieści na wykresie. Są na to trzy sposoby. Pierwszy to zmniejszenie czcionki opcją cex=x, co relatywnie zmniejszy także elementy graficzne. Drugi, to zmniejszenie odstępu między kolejnymi wierszami legendy opcją y.intersp=x, gdzie domyślnie x=1, a trzeba użyć liczby mniejszej. Trzeci, to napisanie legendy w dwóch lub więcej kolumnach. Służy do tego opcja ncol=n. Wygląda to następująco:
windows(4.5, 2.5)
par(mar=c(3,3,1,4.7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:10), type="l", col=rainbow(10),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
legend=c("-5", "0", "5", "10", "15", "20", "25","30", "35", "40"),
title="Temp.", lty=1:8, seg.len=1, col=rainbow(10))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,4.7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:10), type="l", col=rainbow(10),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
cex=0.8,
legend=c("-5", "0", "5", "10", "15", "20", "25","30", "35", "40"),
title="Temp.", lty=1:8, seg.len=1, col=rainbow(10))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,4.7), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:10), type="l", col=rainbow(10),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
y.intersp=0.8,
legend=c("-5", "0", "5", "10", "15", "20", "25","30", "35", "40"),
title="Temp.", lty=1:8, seg.len=1, col=rainbow(10))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,7.5), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:10), type="l", col=rainbow(10),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
ncol=2,
legend=c("-5", "0", "5", "10", "15", "20", "25","30", "35", "40"),
title="Temp.", lty=1:10, seg.len=1, col=rainbow(10))
|
Program tworzy trzy wykresy:
Pierwszy z wykresów pokazuje sytuację, gdy legenda nie mieści się na wykresie. Drugi i trzeci wykres obrazuje efekt zmniejszenia czcionki i odstępów między wierszami legendy. Czwarty wykres pokazuje legendę dwukolumnową.
W przypadku wielokolumnowych legend (ale nie tylko) może przydać się opcja x.intersp=x. Określa ona wielkość odstępu miedzy elementem graficznym (znacznikiem, linią lub prostokątem ze wzorem), a wyjaśnieniem słownym. W wielokolumnowych legendach może wyraźnie zmniejszyć ich szerokość. Można to zobaczyć za pomocą programu:
windows(4.5, 2.5)
par(mar=c(3,3,1,7.5), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:14), type="l", col=rainbow(14),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
ncol=2,
legend=c(paste(1:14*2)),
title="Temp.", lty=1:10, seg.len=1, col=rainbow(14))
#
windows(4.5, 2.5)
par(mar=c(3,3,1,6.5), mgp=c(1.8,0.5,0), xpd=TRUE)
matplot(1:5, outer(1:5,1:14), type="l", col=rainbow(14),
main="", xlab="Podpis osi 0X", ylab="Podpis osi 0Y")
legend(5.3, sum(par("usr")[3:4])/2, xjust=0, yjust=0.5,
ncol=2, x.intersp=0.1,
legend=c(paste(1:14*2)),
title="Temp.", lty=1:10, seg.len=1, col=rainbow(14))
|
Program generuje następujące wykresy:
Legenda związana z różnymi kolorami wypełnienia i teksturą
Obszary wypełnione różnymi kolorami występują w wykresach kołowych uzyskanych funkcja pie(), w wykresach słupkowych uzyskanych funkcją barplot() i w wykresach pudełkowych uzyskanych funkcją boxplot(). W wykresach tworzonych przez funkcje pie() i barplot() można utworzyć namiastkę tekstury stosując wypełnienie obszarów liniami o różnych kolorach, grubościach, kształtach i rodzajach, mające różne nachylenie do osi 0X. Te różne wypełnienia powinny zostać powtórzone w legendzie i wyjaśnione.
Rząd prostokącików wypełnionych zadanymi kolorami wstawia się do legendy za pomocą opcji fill=c(“kolor_1″,…,”kolor_n”). Można przy okazji zmieniać kolor obramowania prostokącików opcją border=”kolor”, co może czasem się przydać. Działanie tych opcji pokazuje następujący program:
windows(4.5, 2.5)
par(mar=c(2,0,0,7), xpd=TRUE)
pie(c(3,4,3,2,5,2), col=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc",
"#ccffcc", "#ccccff"))
legend(1.3,0, xjus=0, yjust=0.5,
fill=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc",
"#ccffcc", "#ccccff"),
legend=c("bór dębowy", "las mieszany", "las liściasty", "las iglasty",
"łęg podmokły"))
#
windows(4.5, 2.5)
par(mar=c(2,0,0,7), xpd=TRUE)
pie(c(3,4,3,2,5,2), col=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc",
"#ccffcc", "#ccccff"), border=c("#ffff00", "#ff11ff", "#11ffff", "#ff1111",
"#11ff11", "#1111ff"),)
legend(1.3,0, xjus=0, yjust=0.5,
fill=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc", "#ccffcc", "#ccccff"),
border=c("#ffff00", "#ff11ff", "#11ffff", "#ff1111", "#11ff11", "#1111ff"),
legend=c("bór dębowy", "las mieszany", "las liściasty",
"las iglasty", "łęg podmokły"))
#
windows(4.5, 2.5)
par(mar=c(2,0,0,7), xpd=TRUE)
pie(c(3,4,3,2,5,2), col=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc",
"#ccffcc", "#ccccff"), border=NA)
legend(1.3,0, xjus=0, yjust=0.5,
fill=c("#ffffcc", "#ffccff", "#ccffff", "#ffcccc", "#ccffcc", "#ccccff"),
border=NA,
legend=c("bór dębowy", "las mieszany", "las liściasty", "las iglasty",
"łęg podmokły"))
|
Powstają trzy wykresy:
W funkcji pie() i barplot() możemy zastosować namiastkę tekstury poprzez zastosowanie opcji angle=x i density=y. Takie same opcje z tymi samymi wartościami należy zastosować w legendzie. Jeżeli tekstura na wykresie słupkowym powstaje poprzez nakładanie ukośnych linii tak samo należy ją nałożyć w legendzie. Kolory tekstury wskazuje się opcją fill=””.
windows(4.5, 2.5)
par(mar=c(2,0,0,7), xpd=TRUE)
pie(c(3,4,3,5), col=c("#131313", "#363636", "#575757", "#797979"),
angle=1:4*30, density=2:5*5)
legend(1.3,0, xjus=0, yjust=0.5,
fill=c("#131313", "#363636", "#575757", "#797979"),
angle=1:4*30, density=2:5*5,
legend=c("PCBs", "HCHs", "HCB", "DDE"))
#
windows(4.5, 2.5)
y=c("A"=4,"B"=7,"C"=1,"D"=3,"E"=5,"F"=2)
par(mar=c(3,3,1,6), mgp=c(1.7,0.5,0), xpd=TRUE)
barplot(y, col=c("#ffcccc", "#ccccff", "#ccffcc"))
barplot(y,angle=c(0,45,90),density=20, col=c("red", "blue", "green3"), add=TRUE)
barplot(y,angle=c(0,135,0),density=20, col=c("red", "blue", "green3"), add=TRUE)
legend(7.5, 5, legend=c(" ", " ", " "),
fill=c("#ffcccc", "#ccccff", "#ccffcc"), bty="n")
legend(7.5, 5, legend=c(" ", " ", " "),
angle=c(0,45,90), density=20, fill=c("red", "blue", "green3"), bty="n")
legend(7.5, 5, legend=c("czerwony", "niebieski", "zielony"),
angle=c(0,135,0), density=20, fill=c("red", "blue", "green3"), bty="n")
|
Powyższy program generuje wykresy postaci:
Wspólna legenda do rycin złożonych z wielu wykresów
Pewne kłopoty może sprawić konieczność umieszczenia legendy na marginesie określonym przez parametr oma=c(x1,x2,x3,x4) funkcji par() wokół ryciny złożonej z kilku wykresów. Pokazuje to następujący przykład:
windows(4.5,2.5)
par(mar=c(1,1,0.5,2.5), mfrow=c(1,2),oma=c(1,1,1,5),xpd=TRUE)
barplot(c(3,2,6,3,1,2),col=c("green","blue","red"))
barplot(c(5,2,4,3,6,3),col=c("green","blue","red"))
legend (7.5,5,legend=c("zielony","niebieski","czerwony"),
fill=c("green","blue","red"))
|
Powstaje rycina postaci:
Legenda ujawnia się tylko na marginesie wyznaczonym przez opcje mar=c() a nie opcję oma=C(). Zbyt duża wartość odpowiedniego marginesu opcji mar=c(), taka żeby zmieścić legendę, powoduje brzydką dużą przerwę między wykresami. Zaradzić można temu bardzo prosto zmieniając wartość opcji xpd=TRUE na xpd=NA.
windows(4.5,2.5)
par(mar=c(1,1,0.5,1), mfrow=c(1,2),oma=c(1,1,1,5),xpd=NA)
barplot(c(3,2,6,3,1,2),col=c("green","blue","red"))
barplot(c(5,2,4,3,6,3),col=c("green","blue","red"))
legend (7.5,5,legend=c("zielony","niebieski","czerwony"),
fill=c("green","blue","red"))
|
Spowoduje to powstanie następującego wykresu:
Przegląd podrzędnych funkcji graficznych
Wykaz podrzędnych funkcji graficznych
Funkcje graficzne podrzędne, zwane inaczej dokładającymi, same z siebie nie tworzą wykresu. Służą do nakładania na wykres znajdujący się w aktywnym oknie różnych elementów. W podstawowym pakiecie graphics są to:
- Funkcje dokładające serie danych w postaci punktów lub linii:
- points()
- lines()
- abline()
- Funkcje dokładające tekst:
- text()
- mtext()
- title()
- Funkcje dokładające zasadnicze części wykresu (osie, legendę, obramowania, siatkę):
- axis()
- rug()
- legend()
- box()
- grid()
- Funkcje dokładające pozwalające na narysowanie na wykresie mniej lub bardziej złożonych figur geometrycznych:
- segments()
- arrows()
- rect()
- polygon()
Wszystkie te funkcje wymagają określenia miejsca, gdzie ma pojawić się określony element. Większość posługuje się współrzędnymi pola kreślenia, ale są też funkcje posługujące się numerem marginesu i numerem linijki określającej odległość na danym marginesie od pola kreślenia. Funkcje box() i grid() odczytują położenie pola kreślenia, nie mają zatem współrzędnych obowiązkowych.
Funkcje posługujące się współrzędnymi pola kreślenia używają nazw zaczynających się od x na współrzędne odczytywane na osi poziomej i y na współrzędne odczytywane na osi pionowej. Są to początkowe argumenty funkcji graficznych podrzędnych i wstawiając odpowiednie wartości na właściwym miejscu ich formalne nazwy można pominąć. Wykaz nazw formalnych argumentów funkcji graficznych podrzędnych posiłkujących się bezpośrednio lub pośrednio współrzędnymi pola kreślenia pokazuje następująca tabela:
Funkcja i jej obowiązkowe argumenty |
Uwagi |
points(x,y)
|
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
lines(x,y)
|
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
abline(b,a)
|
a,b - współczynniki prostej ax+b wykreślanej w polu kreślenia. |
text(x,y,tekst)
|
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, tekst - wektor tekstowy, długości wektorów x,y,tekst muszą być równe. |
legend(x,y,tekst)
|
x - współrzędna na osi poziomej, y - współrzędna na osi pionowej, tekst - wektor tekstowy, Wektory x i y muszą być jednoelementowe. |
segments(x0, y0, x1, y1)
|
x0 - wektor współrzędnych na osi poziomej, y0 - wektor współrzędnych na osi pionowej, x1 - wektor współrzędnych na osi poziomej, y1 - wektor współrzędnych na osi pionowej, długości wektorów x0, y0, x1, y1 muszą być równe. |
arrows(x0, y0, x1, y1)
|
x0 - wektor współrzędnych na osi poziomej, y0 - wektor współrzędnych na osi pionowej, x1 - wektor współrzędnych na osi poziomej, y1 - wektor współrzędnych na osi pionowej, długości wektorów x0, y0, x1, y1 muszą być równe. |
rect(xleft, ybottom, xright, ytop)
|
xleft - wektor współrzędnych na osi poziomej, ybottom - wektor współrzędnych na osi pionowej, xright - wektor współrzędnych na osi poziomej, ytop - wektor współrzędnych na osi pionowej, długości wektorów xleft, ybottom, xright, ytop muszą być równe. |
polygon(x,y)
|
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
Wszystkie wymienione funkcje nie dają żadnej informacji o tym, że użyte współrzędne nie mieszczą się w wykreślonym polu kreślenia lub na całym wykresie. Po prostu nie rysują na wykresie tego, co się na nim nie mieści.
Wykaz nazw formalnych argumentów funkcji graficznych podrzędnych posiłkujących się numerami marginesu i linijki pokazuje następująca tabela:
Funkcja i jej obowiązkowe argumenty |
Uwagi |
axis(side)
|
side - jedna z liczb 1, 2, 3, 4 pokazująca, na której krawędzi pola kreślenia ma być umiejscowiona oś. |
rug(x, ticksize, side)
|
x - wektor punktów, ticksize y - długość znacznika, side jedna z liczb 1,2,3,4 pokazująca, na której osi maja byc znaczniki. |
mtext(text, side, line)
|
text - zmienna tekstowa side - jedna z liczb 1,2,3,4 pokazująca, na którym marginesie ma się pokazać tekst, line - linijka, w której ma sie pokazać tekst. |
title(main, sub,
xlab, ylab, line)
|
main="tekst" oznacza tekst napisany na marginesie górnym sub="tekst" oznacza tekst napisany na marginesie dolnym, xlab="tekst" oznacza tekst napisany na marginesie dolnym, ylab="tekst" - oznacza tekst napisany na marginesie lewym, line oznacza linijke tekstu, w której napisany będzie tekst. |
Zastosowanie funkcji points(), lines(), text(), mtext(), title(), axis(), rug(), legend(), box() i grid() zostało już pokazane w poprzednich rozdziałach. Funkcja abline() będzie pokazana w rozdziale o liniach trendu i regresji liniowej. W dalszej części pokazano zastosowanie pozostałych podrzędnych funkcji graficznych wymienionych w wykazie na początku rozdziału.
Funkcja segments()
Funkcja segments() umożliwia narysowanie na wykresie odcinka jednego lub kilku. Jej obowiązkowymi argumentami są współrzędne punktu początkowego odcinka x0, y0 i współrzędne punktu końcowego odcinka x1 i y1. Wielkości x0, y0, x1 i y1 mogą być wektorami o jednakowej długości i wtedy funkcja segments() wykreśli tyle odcinków, ile jest liczb w każdym z tych wektorów. Pierwsze liczy tych wektorów określają współrzędne końców odcinka pierwszego, drugie to współrzędne końców odcinka drugiego itd.
segments(x0, y0, x1, y1, col=”black”, lty=1, lwd=1)Zdarza się, że na jakiś wykresach chcemy wskazać szczególne punkty i je dodatkowo objaśnić. Wtedy objaśnienie umieszczany w wolnym miejscu na wykresie, a funkcja segment wykreślamy odcinki od objaśnienia do określonych elementów wykresu. Tak jak to pokazano na poniższym wykresie charakteryzującym sezon lęgowy mazurków (dla 250 gniazd kontrolowanych przez wszystkie dni kwietnia określono dzień, w którym zostało zniesione pierwsze jajo).
x=c(0.41, 1.63, 2.44, 3.75, 1.63, 4.64, 4.72, 2.12, 4.48, 4.89, 5.62, 3.42,
6.11, 6.51, 6.60, 6.11, 4.89, 4.32, 4.48, 4.40, 3.26, 2.61, 2.04, 2.28,
2.20, 1.47, 1.30, 0.81, 0.57, 0.33)
windows(4.5, 2.5)
par(mar=c(3,3.5,0.5,0.5), mgp=c(1.7, 0.5, 0))
a=barplot(y, ylim=c(0,10),xlab="Kolejne dni kwietnia",
ylab="Procent rozpoczętych \nzniesień")
axis(1, at=a, labels=1:30, tck=-0.03)
segments(c(a[8],a[8],a[8]),c(8,8,8),c(a[5],a[8],a[12]),c(2,3,4), col="blue")
text(a[8], 8.5, "Gwałtowne opady", col="blue")
|
Program ten generuje następujący wykres:
W programie tym wykorzystano fakt, że funkcja barplot() obok wykresów generuje też współrzędne punktów będące środkami wykreślonych słupków.
Funkcja arrows()
Funkcja arrows(), jak sama nazwa wskazuje, umieszcza na wykresie strzałki, czyli odcinki zakończone grotem, narysowanym jako para segmentów o jednakowej długości wychodzących z końca odcinka i nachylonych do niego pod tym samym kątem. Przypomina ona nieco funkcję segments(), gdyż jej obowiązkowymi parametrami są współrzędne początku x0, y0 i współrzędne końca x1, y1 strzałki. Mogą to być wektory, gdy w programie należy narysować kilka strzałek. Pierwsze liczby tych wektorów określają współrzędne końców pierwszej strzałki, drugie – to współrzędne końców odcinka drugiej strzałki itd.
Strzałki mogą wskazywać na te punkty wykresu, które trzeba wyjaśnić lub opisać. Przykładowo, poniższy wykres pokazuje dynamikę liczebności populacji, na której wykonano eksperyment polegający na wyławianiu osobników i wypuszczaniu ich w odległości 20 km.
N=c(40, 39, 45, 33, 10, 12, 13, 11, 15, 20, 22, 23, 31, 31, 28, 32, 30, 29,
20, 25, 24, 22, 26, 21, 22, 27, 27, 19, 19, 22, 25, 28, 30, 21, 20, 19, 21, 21,
27, 27, 29, 23, 28, 30, 28, 23, 25, 27, 28, 23)
windows(4.5, 2.5)
par(mar=c(3.3,3.3,0.5,0.5),mgp=c(2.2,0.5,0),las=1,xpd=TRUE, ps=14)
plot(0:49,N, type="l", col="brown", lty=1, lwd=2,
xlab="Czas", xlim=c(0,50), ylab="Liczebność populacji",
ylim=c(0,60), tck=-0.03, las=1)
arrows(c(2,30),c(57,60),c(2,30),c(47,50),col="red", length=0.15, lwd=3)
arrows(c(7,33),c(0,50),c(7,33),c(10,60), col="red", length=0.15, lwd=3)
text(35,55, "Początek i koniec \neksploatacji", adj=0, cex=0.8)
|
Wykres wykonany za pomocą tego programu wygląda następująco:
Do interesujących opcji funkcji arrows() należy length=x określająca długość ramion tworzących grot, angle=x określająca kąt w stopniach między ramionami grota a osią strzałki (domyślnie 30°), oraz code=n przyjmujący wartości 1, 2 i 3 przy czym
- code=1 oznacza że grot utworzy się na końcu (x1, y1)
- code=2 oznacza, że grot utworzy się na końcu (x0, y0)
- code=3 oznacza, że grot utworzy się na obu końcach
Poza tym działają w niej te opcje graficzne, które związane są z grubością i stylem linii.
Funkcja rect()
Funkcja rect() służy do rysowania prostokątów na wykresie. Jej obowiązkowymi opcjami są współrzędne dolnego lewego rogu i współrzędne górnego prawego rogu. Była już wykorzystywana do kolorowania pola kreślenia i najczęściej w tym celu się ją stosuje – aby zaznaczyć obszary interesujących danych. Ponieważ jednak funkcja rect() zamazuje przed nią wprowadzane dane, trzeba je dołożyć (najczęściej ponownie) po jej zastosowaniu.
Liczba jaj znoszona przez pewną populację gołębi miejskich w ciągu roku mogłaby być narysowana następująco:
x=c(2, 22, 34, 55, 55, 46, 50, 44, 30, 10, 9, 8)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
plot(1:12, x, pch=20, xlab="miesiące", ylab="Liczba zniesionych jaj", main="")
rect(0.59,0,2.5, 70, col="#99ccff", border=NA)
rect(2.5,0,5.5, 70, col="#ffffcc", border=NA)
rect(5.5,0,8.5, 70, col="#ccffcc", border=NA)
rect(8.5,0,11.5, 70, col="#ffcccc", border=NA)
rect(11.5,0,12.5,70, col="#99ccff", border=NA)
points(1:12, x, pch=20)
mtext("zima",3,0, adj=0)
mtext("wiosna",3,0, adj=0.23)
mtext("lato",3,0, adj=0.55)
mtext("jesień",3,0, adj=0.85)
|
Wykonanie powyższego zestawu poleceń spowoduje wygenerowanie wykresu:
Funkcja ta ma opcje związane z wypełnianiem wnętrza kreskami nachylonymi pod zadanym kątem i o określonej częstości występowania. Służą do tego opcje density=x i angle=y. Opcja border=”kolor” określa kolor obramowania. Zapis border=NA oznacza rysowanie prostokąta bez obramowania.
W funkcji rect() współrzędne lewego dolnego rogu i współrzędne górnego prawego rogu prostokąta mogą być wektorami równej długości. Umożliwia to wstawienie na wykres kilku jednakowych prostokątów.
Funkcja polygon()
Funkcja polygon() służy do wykreślania dowolnych wielokątów, wypełniania ich zadanym kolorem lub wzorem. Służy przede wszystkim do wykreślania tego, czego nie robią nadrzędne funkcje graficzne. Obowiązkowymi opcjami tej funkcji są: wektor współrzędnych wierzchołków wielokąta odczytanych z osi 0X i wektor współrzędnych wierzchołków wielokata odczytanych z osi 0Y. Oba muszą być równej długości. Współrzędne ostatniego punktu nie muszą pokrywać się ze współrzędnymi pierwszego punktu, gdyż domyślnie zawsze ostatni punkt łączony jest z pierwszym.
Funkcja polygon(), mimo, że nie kreśli elementów graficznych standardowo umieszczanych na wykresach, jest bardzo często stosowana. Przykładowo za jej pomocą można “narysować” tło wykresu kojarzące zrobione opracowanie z gatunkiem, który był badany. Robi się to często na posterach. Wygląda to następująco:
x=c(0,0,1,6,9,12,14,17,19,20,19,18,17,19,17,18,19,19,20,20,21,22,21,21,
22,22,23,24,30,27,25,26,26,27,28,28,29,30,31,32,31,33,35,36,37,44,44,37,36,
35,33,29,23,17,16,14,13,13,12,10,9,7,5,3,1)
y=c(7,6,5,5,6, 6, 7, 7, 6, 5, 4, 4, 3, 3, 1, 1, 2, 0, 1, 3, 2, 2, 3, 4, 5, 6, 6,
7, 7, 6, 5, 5, 4, 4, 5, 3, 5, 6, 5, 5, 6, 7, 9, 13, 14, 18, 19, 16, 16, 18,
20, 22, 22, 19, 21, 21, 20, 23, 22, 20, 18, 16, 14, 12, 8)
xu=c(12,14,15,15,16,17,17,16,14,12)
yu=c(15,18,17,14,14,16,19,21,21,19)
xu2=c( 9,10,12,13,13,12,10)
yu2=c(18,18,19,20,23,22,20)
xo=c( 6,7,9,10, 9, 7)
yo=c(10,9,9,10,11,11)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03, bg="#ffe0b5")
plot(3:10, c(10, 20, 16, 27, 22, 33, 34, 28), type="l",lwd=2, xlab="Czas [mies]",
ylab="Liczebność", main="")
wsp.x=(par("usr")[2]-par("usr")[1])/44
wsp.y=(par("usr")[4]-par("usr")[3])/23
polygon(x*wsp.x+par("usr")[1],y*wsp.y+par("usr")[3], col="#eecaa3", border=NA)
polygon(xu*wsp.x+par("usr")[1],yu*wsp.y+par("usr")[3], col="#e3bb95", border=NA)
polygon(xu2*wsp.x+par("usr")[1],yu2*wsp.y+par("usr")[3], col="#e3bb95",
border=NA)
polygon(xo*wsp.x+par("usr")[1],yo*wsp.y+par("usr")[3], col="#e3bb95", border=NA)
lines(3:10, c(10, 20, 16, 27, 22, 33, 34, 28), lwd=3)
box()
|
Wykres uzyskany za pomocą tego programu wygląda następująco:
Znawcy rozpoznają na tym wykresie myszarkę leśną, inni domyślą się, że chodzi o jakąś mysz, a wykres pokazuje jej dynamikę liczebności.
Funkcja podrzedna graficzna utworzona przez użytkownika R
Funkcja polygon() nadaje się do utworzenia takiego wykresu kołowego, jaki tworzy funkcja pie(), ale bez jej ograniczeń (niemożność jej umieszczenia na inaczej podkolorowanym polu kreślenia, niemożliwość nałożenia na wycinki koła kilku kreskowych deseni). Problemy te rozwiązuje poniższa funkcja tworząca wykres kołowy na utworzonym wcześniej wykresie, za pomocą odpowiednio zestawionych “wielokątów” imitujących wycinki kołowe. Wygląda ona następująco:
#Funkcja graficzna podrzędna
#domalowywujaca wykres kołowy w środku wykresu.
pieplot = function(dane, radius=1, init.angle=0,
col=gray(1:length(dane)/length(dane)),
density=rep(NULL, length(dane)),
angle=rep(1:length(dane)*(180/length(dane)))) {
plot.window(c(-1,1), c(-1,1), asp=1)
alpha=dane/sum(dane)*(2*pi)
beta=c(0,cumsum(alpha)[1:(length(dane)-1)])+init.angle
x0=radius*cos(init.angle)
y0=radius*sin(init.angle)
xp=x0
yp=y0
for(i in 1:length(dane)){
j=1
x=c(0,x0)
y=c(0,y0)
while (j*pi/1000<alpha[i]) {
x=c(x, radius*cos(j*pi/1000+beta[i]))
y=c(y, radius*sin(j*pi/1000+beta[i]))
j=j+1}
if (i<length(dane)) {x0=radius*cos(beta[i+1])
y0=radius*sin(beta[i+1])}
if (i==length(dane)) {x0=xp
y0=yp}
x=c(x,x0)
y=c(y,y0)
polygon(x,y, col=col[i], density=density[i], angle=angle[i])}}
|
Funkcja ta nie ma wszystkich opcji graficznych, jakie zazwyczaj mają funkcje graficzne w R, ale osoby trochę już programujące z łatwością mogą zmodyfikować jej kod. Jej użycie wygląda następująco:
windows(4.5, 2.5)
par(mar=c(1.5,1.5,1.5,6), mgp=c(0.2,0,0), bg="#ffcccc")
plot(1:10, type="n", axes=FALSE, xlab="Udział dużych ssaków", ylab="",
main="Puszcza Kampinoska", cex.main=0.9, font.main=1)
grid(100,50,lty=1,lwd=10,col="#ffeeee")
pieplot(c(2000,700,200,70,54,390,95,3,12), col=rainbow(9), density=1:9*10,
angle=1:9*180/9)
pieplot(c(2000,700,200,70,54,390,95,3,12), col=rainbow(9), density=1:9*10,
angle=-(1:9*180/9))
par(xpd=TRUE)
legend(par("usr")[2]+0.1,sum(par("usr")[3:4])/2, bty="n", fill=rainbow(9),
density=1:9*10, angle=1:9*180/9, xjust=0, yjust=0.5,
legend=c("sarna","dzik", "łoś", "jeleń", "jenot", "lis", "borsuk", "wydra",
"ryś"))
legend(par("usr")[2]+0.1,sum(par("usr")[3:4])/2, bty="n", fill=rainbow(9),
density=1:9*10, angle=-(1:9*180/9), xjust=0, yjust=0.5,
legend=c("","", "", "", "", "", "", "", ""))
|
Powstanie w ten sposób następujący wykres:
Zapisywanie wykonanego wykresu
Metody zapisu wykresu
Zapis wykonanego wykresu w R jest pozornie bajecznie prosty i nie wymaga wyjaśnień. Kiedy uaktywnimy wykres (co można rozpoznać po ciemniejszym niebieskim obramowaniu) można go skopiować do pamięci (Ctrl+C) i wywołać w dowolnym programie graficznym. Przenosi się jako bipmapa. Dopiero przy bardzo dużym powiększeniu wykresu widać, że nie jest ona wysokiej jakości. Znacznie lepiej jest kliknąć na “Plik” i wybrać z menu “Zapisz jako”.
Pojawia się 7 podstawowych formatów zapisu plików graficznych rozpoznawalnych przez większość popularnych programów. Różnią się one rozmiarem tworzonego pliku. Można to prześledzić zapamiętując w różnych formatach ten sam wykres: plot(1:10) bez dodatkowych opcji.
Format |
Rozmiar w bajtach |
Metafile |
16 384 |
Postscript |
3 962 |
|
|
1 765 |
Png |
3 341 |
Bmp |
451 990 |
TIFF |
1 352 876 |
Jpeg (100%) |
27 481 |
Ze względu na to, że jakość obrazu cyfrowego zależy od liczby pikseli opisanych w pliku, można się spodziewać zależności: im większy rozmiar tym większa jakość. Nie do końca jest to prawda. Wynika to z różnego przeznaczenia plików graficznych i różnego sposobu programowania przez nie cyfrowego obrazu.
Format metafile a właściwie windows metafile zawiera instrukcje dla systemu operacyjnego o tym, jak wyświetlać grafikę wektorową i rastrową. Zawiera te same informacje, co bipmapa, ma tę samą jakość, ale mniejszy rozmiar.
Format postscript to jedyny format w R pozwalający zapamiętać wykres w grafice wektorowej. Oznacza to, że wszystkie elementy wykresu zapamiętywane są w postaci wzorów matematycznych i odtwarzane z taką samą jakością przy dowolnym powiększaniu wykresu. Często jest to format o który proszą wydawnictwa naukowe i będzie jeszcze o nim mowa w dalszych podrozdziałach. Generalnie format ten tworzy wykresy najwyższej jakości, zwłaszcza gdy są one zmniejszane, powiększane i wyświetlane na różnych komputerach.
Format PDF powstał głównie po to by można było oglądać i czytać pliki o tym formacie w różnych systemach operacyjnych. Rozpowszechnione bezpłatne oprogramowanie firmy Adobe przeznaczone do czytania tych plików spowodowało, że jest to najbezpieczniejszy format do zapamiętywania gotowych prac tekstowo-graficznych, gdy mają być one odtwarzane na różnych komputerach. W mniejszym stopniu zwraca się w nim uwagę na jakość wykresów, ale w ostatnich wersjach Adobe-Akrobat jest ona całkiem wysoka.
Png jest formatem plików graficznych, w którym elementy obrazu zapisywane są rastrowo i stosowana jest ich bezstratna kompresja. Nadaje się bardzo dobrze do zapamiętywania wykresów, gdyż nie wprowadza cieniowań prostych i punktów. Ponadto pliki te nie są duże i nie zwiększają zanadto rozmiarów prac dyplomowych po ich skopiowaniu.
Bmp jest formatem obrazów utworzonych przez stosunkowo prosty program, który poszczególnym pikselom (współrzędnym punktów na ekranie) przyporządkowuje odpowiedni kolor. Ma dobrą jakość dla wykresów o końcowym formacie. Przy konieczności powiększania, a także zmniejszania obrazu jego jakość szybko maleje. Ma na ogół duży rozmiar i wszelkie kompresje bezstratne niewiele go zmniejszają.
TIFF to bardzo rozbudowany format plików graficznych rastrowych przechowujący informacje o kanałach alfa, ścieżkach, profilu kolorów, komentarzach. Jedyny format rastrowy, który może być zamieniany na wektorowy przez odpowiednie programy postscriptowe. Dobrze sprawdza się to tylko na wykresach. Często taki format wykresów jest wymagany przez wydawnictwa naukowe.
Jpeg jest zarówno formatem plików rastrowych jak i algorytmem kompresji obrazów cyfrowych do plików graficznych mających mniejszy rozmiar niż pliki pierwotne. Stosowany jest głównie do zdjęć i rysunków, w mniejszym stopniu do wykresów, gdyż kompresja punktów i linii prostych rozmywa je nieco i daje wyrażny cień. Ma jednak możliwość określania jakości tej kompresji i w tym wypadku zasada: “większa jakość – większy rozmiar”, sprawdza się.
Na dzień dzisiejszy najlepiej sprawdzają się wykresy o formacie png, gdy chcemy je skopiować do pracy dyplomowej.
Zapis wykresu w formacie postscript
Wydawnictwa naukowych po przyjęciu pracy do druku życzą sobie dobrej jakości zdjęć i wykresów umieszczanych w tej pracy. Wykaz możliwych formatów elementów graficznych można znaleźć na stronach internetowych tych wydawnictw. Wśród możliwych formatów wykresów zawsze pojawia się format Encapsulated PostScript czyli pliki postscript z rozszerzeniem .ps lub częściej .eps. W żargonie wydawniczym wykresy te nazywa się EPSami.
Zapis wykresu w formacie postscript to własnie zrobienie EPSu. Wykres taki ma rozszerzenie .eps, nie można go zobaczyć poprzez uruchomienie popularnych plików graficznych takich jak IrfanView, Photoshop, Gimp lub systemowych plików do oglądania zdjęć. Dopiero programy czytające grafikę wektorową (najpopularniejszy z nich to Incscape i Latex z biblioteką epstopdf) otwierają je w prawidłowo.
Zapis wykresu w formacie EPS poprzez wybranie postscript w menu “Zapisz jako”, ma jednak pewne ograniczenia. Na przykład elementy tekstu przekształcone funkcją expression() (patrz: rozdział 8) nie zawsze są prawidłowo przekształcane do języka postscript.
windows(4.5, 2.5)
par(mar=c(3.4,3.4,1.5,0.5),mgp=c(1.7,0.5,0), tck=-0.03)
plot(1:10,type="n",
xlab=expression(alpha*beta*gamma*delta*epsilon*zeta*theta*iota*kappa*lambda*mu*
nu*xi*pi*rho*sigma*tau*upsilon*phi*chi*psi*omega),
main=expression(Alpha*Beta*Gamma*Delta*Epsilon*Zeta*Theta*Iota*Kappa*Lambda*Mu*
Nu*Xi*Pi*Rho*Sigma*Tau*Upsilon*Phi*Chi*Psi*Omega),
ylab=expression("objętość komórki [ "*mu*m^3*" ]"))
text(1, 7, expression(bar(x)*" = "*frac(1, n)*sum(x[i], i==1, n)), cex=1.4,
adj=0)
text(5, 4, expression(paste(frac(1, sigma*sqrt(2*pi))*" "*
plain(e)^{frac(-(x-mu)^2, 2*sigma^2)})), cex=1.4, adj=0)
|
Powyższy kod daje wykres, którego format png widoczny jest z lewej, a postscript otwarty przez Latex w środku i Inkscape z prawej. Oba wykresy poscriptowe są tu pokazane po exporcie do formatu png, co pogarsza ich jakość, ale nie zmienia tego co jest widoczne w redakcjach: braku niektórych polskich liter. Z kolei Inkscape nie czyta litery μ.
Trzeba przyznać, że z każdą nową wersją R, coraz lepiej przekształcany jest format matematyczny tworzony w R na język postscriptowy. Nadal jednak mogą pojawić się istotne błędy.
Język postscript posiada kilka własnych krojów czcionek nie do końca zgodnych z czcionkami systemowymi. Dlatego też każdy krój czcionki wybrany z systemu do zrobienia wykresu w R powoduje, że zapis takiego pliku jako typ poscript generuje błąd i albo tworzy pusty rysunek albo zawiesza się. Można to sprawdzić używając programu:
windowsFonts(Arial = windowsFont("Arial"),
times = windowsFont("Times New Roman"),
Symbol = windowsFont("Symbol"))
#
windows(4.5, 2.5)
par(mar=c(1,1,1,1), ps=20, bg="yellow")
plot(1:10, type="n", axes=FALSE, xlab="", ylab="")
par(family="times")
text(1,7, "Źrebak złamał kość", adj=0)
par(family="Arial")
text(8,7, "Times New Roman", adj=0, cex=0.5)
par(family="Symbol")
text(1,4,"abcdefghijklmnoprstuvwxyz", adj=0)
par(family="Arial")
text(8,4, "Symbol", adj=0, cex=0.5)
|
W następnym podrozdziale powiemy jak mają postępować osoby, które spotkały się w wymogami redakcyjnymi typu:
1. Typ czcionki: Times New Roman
2. Format wykresów: Wyłącznie poscript (lub wyłącznie eps)
Tworzenie wykresu za pomocą funkcji postscript()
Zapisywanie wykresu w formacie postscript przy użyciu menu R to nie jedyny sposób na wykonanie EPSu. Można to samo, lub prawie to samo zrobić używając funkcji postscript(). Ponieważ nasz wykres będzie wtedy składał się wyłącznie z poleceń postscriptowych, musimy zapomnieć w nim o używaniu czcionek i innych elementów systemowych właściwych dla naszego komputera. Nie można wtedy też użyć funkcji windows() na określnie wymiarów wykresu. Określa się je opcjami width=n1, height=n2 funkcji postscript(). Wśród opcji tej funkcji jest encoding, za pomocą której można określić strony kodowe dla znaków narodowych. Dla polskich znaków jest to “ISOLatin2.enc”.
postscript("d:Fig11c.eps", width=4.5, height=2.5, encoding="ISOLatin2.enc")
par(mar=c(1,1,1,1))
plot(1:10, type="n", xlab="", ylab="")
text(1,9, "Źrebak złamał kość, bo lękał się bąka", col="red", adj=0)
text(1,7, "ŹREBAK ZŁAMAŁ KOŚĆ, BO LĘKAŁ SIĘ BĄKA", col="red", adj=0)
text(1,4, expression(alpha*beta*gamma*delta*epsilon*zeta*theta*iota*kappa*lambda*
mu*nu*xi*pi*rho*sigma*tau*upsilon*phi*chi*psi*omega), col="blue", adj=0)
dev.off()
|
Powstaje na dysku D: (o ile ktoś ma taki dysk lub partycję) plik eps, który otworzony poprzez Latex i Inkscape wygląda następująco:
Najwyraźniej niemożność odczytania postscriptowego μ jest wadą Inscape’a, nie programu R. Oglądanie EPSów w Latexu przed wysłaniem ich do redakcji jest standardem. Właśnie za pomocą programu zgodnego z Latexem redakcja będzie przygotowywała artykuł do druku. Polskie oraz greckie litery są wyświetlane prawidłowo. Czcionka której domyślnie używa funkcja postcript nosi nazwę helvetica i prawie nie różni się od czcionki systemowej arial.
Zmianę domyślnej czcionki umożliwia opcja family funkcji postscript(). Najpopularniejwsze, zaimplementowane do większości sprzętu drukującego prace, noszą nazwy “AvantGarde”, “Bookman”, “Courier”, “Helvetica”, “Helvetica-Narrow”, “NewCenturySchoolbook”, “Palatino” or “Times”. Modyfikacje tych krojów (pogrubienie, pochylenie) uzyskamy za pomocą opcji font mogącą przyjmować wartości od 1 do 5.
postscript("d:Fig11d.eps", width=4.5, height=2.5,
encoding="ISOLatin2.enc", family="AvantGarde")
par(mar=c(1,1,1,1))
plot(1:10, type="n", xlab="", ylab="")
text(5.3,9, "AvantGarde", adj=0.5)
par(font=1)
text(1,8, "Ala ma kota, a źrebak złamał kość", adj=0)
par(font=2)
text(1,7, "Ala ma kota, a żebrak złamał kość", adj=0)
par(font=3)
text(1,6, "Ala ma kota, a źrebak złamał kość", adj=0)
par(font=4)
text(1,5, "Ala ma kota, a żebrak złamał kość", adj=0)
par(font=5)
text(1,4, "Ala ma kota, a źrebak złamał kość", adj=0)
dev.off()
|
Po zmianie nazwy kroju czcionki w funkcji postscript() i pierwszej funkcji text() na kolejne popularne czcionki postscriptowe (poza domyślną Helvetica) uzyskano następujące wykresy (kopie tego co pokazał program Latex zapamiętane w formacie png):
Widać, że opcja font=5 umożliwia wstawianie greckich liter do tekstu. Ponadto wszystkie popularne czcionki dobrze odczytują znaki strony kodowej “ISOLatin2.enc” co umożliwia używanie polskich liter.
Czcionka “Times” jest zgodna z często zalecanym przez redakcje formatem czcionki stosowanej w artykułach, gdyż przy stosunkowo dobrej czytelności tworzy ona najbardziej ściśnięte teksty zajmujące najmniej miejsca. Powyższe przykłady pokazują, jak ją zastosować w EPSach wysyłanych później do redakcji.
Wykresy kołowe, zastosowanie
Uwagi ogólne
Gdy obrazujemy udziały procentowe jakiś kategorii osobników i zależy nam na podkreśleniu różnic w tych udziałach, to stosujemy wykresy kołowe. Przykładowo gdy porównujemy dwa środowiska, w których wyróżniamy 5 kategorii, a w każdej kategorii znajdujemy pewne liczby obiektów, zobrazowanie tego za pomocą nadrzędnej funkcji graficznej pie() może wyglądać następująco:
srodowisko=c("HALA 1", "HALA 2")
kategoria=c("A", "B", "C", "D", "E")
liczby.w.HALA1=c(234, 456, 211, 98, 14)
liczby.w.HALA2=c(54, 28, 78, 43, 2)
#
windows(5, 2.5)
par(mfcol=c(1,2),mar=c(0.5,0.5,1,0.5))
pie(liczby.w.HALA1, col=rainbow(10)[c(2:4,7,9)], labels=kategoria,
main=srodowisko[1])
pie(liczby.w.HALA2, col=rainbow(10)[c(2:4,7,9)], labels=kategoria,
main=srodowisko[2])
|
Po wykonaniu programu powstanie następujący wykres:
Wykres ten uwidacznia największą różnicę między środowiskami. W środowisku HALA 1 udział procentowy kategorii B i C jest inny niż w środowisku HALA 2.
Graficzne opracowanie skutków katastrofy Tytanika
Wśród na zaimplementowanych do R obiektów jest czterowymiarowa macierz o nazwie Titanic pokazująca liczby osób podróżujących statkiem Tytanik podczas jego pierwszego rejsu zakończonego zderzeniem z górą lodową. Osoby te zostały podzielone na te, które zmarły i te, które przeżyły, na kobiety i mężczyzn, dorosłych i dzieci oraz w zależności od ich statusu majątkowego, czego wskaźnikiem była klasa, którą te osoby podróżowały. Osobną grupę stanowi załoga. Macierz ta wygląda następująco.
> Titanic
, , Age = Child, Survived = No
#
Sex
Class Male Female
1st 0 0
2nd 0 0
3rd 35 17
Crew 0 0
#
, , Age = Adult, Survived = No
#
Sex
Class Male Female
1st 118 4
2nd 154 13
3rd 387 89
Crew 670 3
#
, , Age = Child, Survived = Yes
#
Sex
Class Male Female
1st 5 1
2nd 11 13
3rd 13 14
Crew 0 0
#
, , Age = Adult, Survived = Yes
#
Sex
Class Male Female
1st 57 140
2nd 14 80
3rd 75 76
Crew 192 20
|
Aby przekonać się, którymi zmiennymi są poszczególne wymiary tej macierzy, można zastosować funkcję dimnames().
> dimnames(Titanic)
$`Class`
[1] "1st" "2nd" "3rd" "Crew"
#
$Sex
[1] "Male" "Female"
#
$Age
[1] "Child" "Adult"
#
$Survived
[1] "No" "Yes"
|
Z Takiego układu wynika, że Titanic[,,,”No”] to macierz trójwymiarowa pokazująca liczby osób zmarłych podczas katastrofy, a Titanic[,,,”Yes”] pokazuje liczby osob, które przeżyły. Zapis [1,1,1,”No”] pokazuje liczbę osób zmarłych z pierwszej klasy, dzieci płci męskiej, [1,1,2,”No”] to liczba pasażerów zmarłych z pierwszej klasy dorosłych płci męskiej. Mozna to wykorzystać do przedstawienia proporcji zmarłych i przeżywających katastrofę samych pasażerów w zależności od ich płci i statusu majątkowego (wtedy sumujemy dzieci i dorosłych określonej płci) oraz w zależności od wieku pasażerów i statusu majątkowego (wtedy sumujemy dziewczynki i chłopców oraz dorosłych: kobiety i mężczyzn). Przedstawiono to w następującym skrypcie:
nazwy1 = c("1 klasa", "2 klasa", "3 klasa", "Załoga")
nazwy2 = c("mężczyźni","kobiety")
nazwy3 = c("dzieci", "dorośli")
nazwy4 = c("Zmarli", "Przeżyli")
Titanic1=Titanic[,,"Child",]+Titanic[,,"Adult",]
windows(5, 6)
par(mar=c(0,0,1,0), mgp=c(1.7,0.5,0), mfrow=c(3,2))
for (i in 1:3) for (j in 1:2) pie(c(Titanic1[i,j,"No"],Titanic1[i,j,"Yes"]),
col=c("black", "grey"), labels=nazwy4, ps=12,
main=paste(nazwy1[i],nazwy2[j]))
#
Titanic2=Titanic[,"Male",,]+Titanic[,"Female",,]
windows(5, 6)
par(mar=c(0,0,1,0), mgp=c(1.7,0.5,0), mfrow=c(3,2))
for (i in 1:3) for (j in 1:2) pie(c(Titanic2[i,j,"No"],Titanic2[i,j,"Yes"]),
col=c("black", "grey"), labels=nazwy4, ps=12,
main=paste(nazwy1[i],nazwy3[j]))
|
Skrypt ten generuje następujące zestawienia wykresów kołowych:
Pokazują one zasady jakimi kierują się ludzie w sytuacji, gdy trzeba wybierać kogo ocalić, a kogo nie. Historia nie dała nam bardziej przekonującego dowodu, że w sytuacji, gdy trzeba dokonać takiego wyboru, gatunek nasz skłonny jest chronić najmłodszych, kobiety i także najbogatszych.
Wykresy słupkowe, zastosowanie
Procent ilości wyróżnionych w jakiś sposób danych wśród wszystkich danych pokazuje się w postaci słupków. Układ tych słupków zależy od złożoności danych i sposób wykonania wykresu powinien służyć tylko jednemu celowi: w jak najbardziej przejrzysty sposób odzwierciedlać zarówno sposób prowadzenia badań jak i uzyskane na jego podstawie wyniki. Im mniej czasu czytelnik poświęci na zrozumienie wykresu, tym lepiej.
Badania drobnych ssaków z reguły polegają na rozstawieniu w środowisku pułapek żywołownych z przynętą, ich przeglądach (raz lub dwa razy dziennie), ocenie, ważeniu i znakowaniu złowionych osobników i wypuszczeniu na wolność. Obecnie znakowanie polega na zakładaniu kolczyków lub obrączek na ucho zwierzęcia (gdy celem badań jest długotrwała obserwacja populacji) lub przynajmniej wygoleniu sierści na grzbiecie zwierząt, gdy chce się odróżnić wcześniej złowione osobniki od nowych. Ocena zwierzęcia to określenie jego płci, dojrzałości i aktywności rozrodczej. Podczas takich badań złowiono 81 różnych myszy leśnych w tym 12 niedojrzałych samców, 22 dorosłych, aktywnych samców, 8 niedojrzałych samic, 18 samic dojrzałych, aktywnych i gotowych do rozrodu (tzw. receptywnych), 15 samic w ciąży i 6 karmiących. Jak najlepiej przedstawić strukturę rozrodczą populacji myszy leśnej podczas badań?
Grupa zwierząt |
Skrót |
Liczba zwierząt |
Procent |
Samce niedojrzałe |
m-juv |
12 | 14.8 |
Samce niedorosłe |
m-ad |
22 | 27.2 |
Samice niedojrzałe |
f-juv |
8 | 9.9 |
Samice receptywne |
f-rec |
18 | 22.2 |
Samice ciężarne |
f-preg |
15 | 18.5 |
Samice karmiące |
f-feed |
6 | 7.4 |
Z powyższego zestawienia widać, że skróty wyróżnionych grup zwierząt utworzono z nazw angielskich. Skrót “m” od “male”, “f” od “female”, “juv” od “juvenile”, “ad” od adult itd. Gdy praca jest przygotowywana do tłumaczenia na angielski jest to logiczne. W polskojęzycznych pracach licencjackich i magisterskich należałoby wymyślić polskie odpowiedniki tych skrótów. Skróty są używane na wykresach i w tabelach w pracy, a ich wyjaśnienie powinno znaleźć się w części “metody”. Ponieważ tym razem wykres ma się znaleźć w publikacji, a w poleceniach dla autorów znaleziono, że rozmiary wykresów powinny wynosić 4.5×2.5 cala, a używana czcionka ma mieć krój “Times New Roman”, to należy się zastosować do tych poleceń. Ponadto wydawnictwo życzy sobie wyłącznie wykresów czarno-białych, bez odcieni szarości, więc wszelkie różnice w rodzaju słupków powinny zostać wykonane za pomocą tekstury.
Polecenia związane z wykonaniem wykresu notujemy w skrypcie i ten skrypt zapamiętujemy. Sam wykres można wygenerować tuż przed posłaniem artykułu do druku, już po wszystkich poprawkach.
windows(4.5, 2.5)
windowsFonts(TimesNewRoman = windowsFont("Times New Roman"))
x=c(12,22,8,18,15,6)
par(family="TimesNewRoman", mar=c(3,3,0.5,0.5), mgp=c(1.5,0.5,0), las=1)
barplot(x/sum(x)*100,
angle=c(135,0,45,45,45,45),
density=c(10,20,10,20,50,200),
col="black", names.arg=c("m-juv","m-ad","f-juv","f-rec","f-preg","f-feed"),
xlab="Wyróżnione grupy zwierząt",
ylab="Procent",
ylim=c(0,30))
barplot(x/sum(x)*100,
angle=c(135,90,45,135,135,135),
density=c(10,20,10,20,50,200),
col="black", add=TRUE)
|
Wygenerowany wykres ma następującą postać.
W powyższym wykresie ze względu na podpisy pod słupkami nadawanie różnych wzorów osobnikom różnej kategorii nie jest w zasadzie konieczne. Ale wiąże się to z badaniem drugiego gatunku – nornicy rudej. Złowiło się ich 107 różnych osobników, w tym 35 niedojrzałych samców, 28 dorosłych samców, 22 niedojrzałe samice, 15 samic receptywnych, 4 ciężarne i 3 karmiące. Wykres porównujący struktury płciowe obu gatunków, w najbardziej przystępny sposób pokazujący różnice w całej strukturze, wygenerujemy za pomocą poleceń:
windows(4.5,2.5)
windowsFonts(TimesNewRoman = windowsFont("Times New Roman"))
x=c(12,22,8,18,15,6)
y=c(35,28,22,15,4,3)
x1=x/sum(x)*100
y1=y/sum(y)*100
par(family="TimesNewRoman", mar=c(3,3,0.8,5), mgp=c(1.5,0.5,0), las=1, xpd=TRUE)
#
barplot(cbind(x1,y1),
angle=c(135,0,45,45,45,45),
density=c(10,20,10,20,50,200),
col="black",
axisnames=TRUE,
names.arg=c("mysz leśna","nornica ruda"),
xlab="Dominujące gatunki ",
ylab="Procent")
#
barplot(cbind(x1,y1),
angle=c(135,90,45,135,135,135),
density=c(10,20,10,20,50,200),
col="black",
axisnames=TRUE,
names.arg=c(" "," "),
add=TRUE)
#
legend(2.5, 90,
title=" \n ",
legend=c(" ", " ", " ", " ", " ", " "),
angle=c(135,0,45,45,45,45),
density=c(10,20,10,20,50,200), fill="black", box.col="white")
#
legend(2.5, 90,
title="grupy\n osobników",
legend=c("m-juv", "m-ad", "f-juv", "f-rec", "f-preg", "f-feed"),
angle=c(135,90,45,135,135,135),
density=c(10,20,10,20,50,200), fill="black", box.col="white")
|
W powyższym wykresie wyróżnienie różnych kategorii zwierząt za pomocą różnej tekstury jest konieczne. Zatem analogiczną teksturę wypada używać także na innych wykresach.
Jeszcze inny typ wykresu jest potrzebny do szczegółowego porównania obu gatunków pod względem wielkości frakcji każdej z kategorii osobników. Możliwy byłby wykres uzyskany po niewielkiej modyfikacji kodu:
windows(4.5,2.5)
windowsFonts(TimesNewRoman = windowsFont("Times New Roman"))
x=c(12,22,8,18,15,6)
y=c(35,28,22,15,4,3)
x1=x/sum(x)*100
y1=y/sum(y)*100
par(family="TimesNewRoman", mar=c(3,3,0.8,5), mgp=c(1.5,0.5,0), xpd=TRUE, las=1)
#
barplot(cbind(x1,y1), beside=TRUE,
angle=c(135,0,45,45,45,45),
density=c(10,20,10,20,50,200),
col="black",
axisnames=TRUE,
names.arg=c("mysz leśna","nornica ruda"),
xlab="Dominujące gatunki ",
ylab="Procent")
#
barplot(cbind(x1,y1), beside=TRUE,
angle=c(135,90,45,135,135,135),
density=c(10,20,10,20,50,200),
col="black",
axisnames=TRUE,
names.arg=c(" "," "),
add=TRUE)
#
legend(14.5, 30,
title=" \n ",
legend=c(" ", " ", " ", " ", " ", " "),
angle=c(135,0,45,45,45,45),
density=c(10,20,10,20,50,200), fill="black", box.col="white")
#
legend(14.5, 30,
title="grupy\n osobników",
legend=c("m-juv", "m-ad", "f-juv", "f-rec", "f-preg", "f-feed"),
angle=c(135,90,45,135,135,135),
density=c(10,20,10,20,50,200), fill="black", box.col="white")
|
Opisywana praca skoncentrowana była na zmianach struktury rozrodczej drobnych ssaków leśnych. Gdyby w większym stopniu zależało autorom na porównaniu myszy leśnej z nornicą rudą należałoby opisywane zagadnienie zobrazować inaczej. Poszczególne frakcje osobników jednego i drugiego gatunku powinny występować obok siebie. Należałoby wybrać dwie tekstury i jedną stosować konsekwentnie dla myszy leśnej, drugą dla nornicy rudej. Dwa ostatnie wykresy wyglądałyby następująco:
W pierwszym suma procentów osobników każdej grupy z obu gatunków została wyrównana do 100. Pokazuje on zatem różnice w strukturze np. młodocianych lub ciężarnych samic myszy leśnej i nornicy. W drugim suma procentów osobników z różnych grup dla każdego gatunku została wyrównana do 100 co pozwala porównywać także strukturę rozrodczą obu gatunków, ale akcentując różnice we frakcjach częściej i rzadziej łowionych osobników. Wykresy te zostały wygenerowane za pomocą programów:
windows(4.5,2.5)
windowsFonts(TimesNewRoman = windowsFont("Times New Roman"))
x=c(12,22,8,18,15,6)
y=c(35,28,22,15,4,3)
x1=x/(x+y)*100
y1=y/(x+y)*100
par(family="TimesNewRoman", mar=c(3,3,0.8,6), mgp=c(1.5,0.5,0), xpd=TRUE, las=1)
#
barplot(rbind(x1,y1),
angle=c(45,0),
density=c(10,20),
col="black",
axisnames=TRUE,
names.arg=c("m-juv", "m-ad", "f-juv", "f-rec", "f-preg", "f-feed"),
xlab="Grupy osobników",
ylab="Procent")
#
barplot(rbind(x1,y1),
angle=c(45,90),
density=c(10,20),
col="black",
axisnames=TRUE,
names.arg=c(" ", " ", " ", " ", " ", " "),
add=TRUE)
#
legend(7.3, 70,
title=" ",
legend=c(" ", " "),
angle=c(45,0),
density=c(10,20), fill="black", box.col="white")
#
legend(7.3, 70,
title="gatunek",
legend=c("mysz leśna", "nornica ruda"),
angle=c(45,90),
density=c(10,20), fill="black", box.col="white")
|
windows(4.5,2.5)
windowsFonts(TimesNewRoman = windowsFont("Times New Roman"))
x=c(12,22,8,18,15,6)
y=c(35,28,22,15,4,3)
x1=x/sum(x)*100
y1=y/sum(y)*100
par(family="TimesNewRoman", mar=c(3,3,0.8,5), mgp=c(1.5,0.5,0), xpd=TRUE, las=1)
#
barplot(rbind(x1,y1), beside=TRUE,
angle=c(45,0),
density=c(10,20),
col="black",
axisnames=TRUE,
names.arg=c("m-juv", "m-ad", "f-juv", "f-rec", "f-preg", "f-feed"),
xlab="Grupy osobników",
ylab="Procent")
#
barplot(rbind(x1,y1), beside=TRUE,
angle=c(45,90),
density=c(10,20),
col="black",
axisnames=TRUE,
names.arg=c(" ", " ", " ", " ", " ", " "),
add=TRUE)
$
legend(17, 30,
title=" ",
legend=c(" ", " "),
angle=c(45,0),
density=c(10,20), fill="black", box.col="white")
#
legend(17, 30,
title="gatunek",
legend=c("mysz leśna", "nornica ruda"),
angle=c(45,90),
density=c(10,20), fill="black", box.col="white")
|
Wykresy pudełkowe, zastosowanie
Wykres pudełkowy dla mediany
Wykres pudełkowy znacznie lepiej od wykresów słupkowych oddaje ideę rozkładu danych w postaci pewnej wartości centralnej i wielkości charakteryzującej zakres skupiania się danych wokół tej wartości. Stosowany jest tylko dla zmiennych liczbowych i przeważnie dla zmiennych ciągłych. Zmienne dyskretne tak charakteryzowane musi cechować duża zmienność potencjalnych wyników (np. może to być liczebność populacji).
Możemy to zobrazować rysując sobie rozkład z dużej próby za pomocą funkcji hist() oraz rysując dla niego wykres pudełkowy za pomocą funkcji boxplot().
x=c(13.75, 7.20, 7.39, 0.60, 12.55, 9.18, 9.21, 14.51, 11.08, 5.57, 10.88, 13.31,
11.47, 9.79, 4.64, 9.85, 12.63, 9.91, 10.23, 6.44, 2.00, 4.73, 13.63, 9.76,
17.93, 7.08, 14.32, 11.21, 10.10, 12.03, 10.43, 9.41, 7.12, 10.75, 10.79,
8.73, 11.53, 12.20, 12.36, 13.88, 10.59, 13.49, 9.57, 10.20, 9.44, 12.76,
11.51, 6.96, 3.90, 13.54, 7.32, 11.16, 12.15, 9.55, 4.50, 4.38, 11.13, 13.07,
7.49, 16.59, 4.40, 8.69, 7.13, 8.61, 8.74, 13.14, 9.60, 6.98, 8.38, 8.96,
11.98, 8.30, 11.26, 8.86, 16.08, 11.36, 6.53, 12.34, 8.76, 14.45, 16.08, 8.43,
11.49, 9.42, 10.66, 12.56, 12.51, 17.82, 8.86, 13.14, 9.74, 7.86, 13.26,
11.17, 10.93, 7.95, 6.16, 6.22, 10.17, 9.84)
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
hist(x, xlab="x", ylab="liczba danych",, main="", breaks=20, xlim=c(0,20),
col="blue")
windows(4.5, 2.5)
par(mar=c(0.5, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(x, range=0, xlab="", ylab="x", col="blue")
|
Efektem wykonania tego programu są dwa wykresy:
Wykres pudełkowy pokazał zakres danych od najmniejszej do największej (pionowa przerywana kreska) oraz w jakim zakresie zmieściła się połowa danych (długość pudełka). Upraszcza (choć jednak także trochę zafałszowuje) interpretację uzyskanych wyników, ale jedocześnie umożliwia porównanie obok siebie kilku rozkładów.
Standardowo, gruba kreska w pudełku, oznacza medianę z próby, dolna krawędź pudełka jest pierwszym kwartylem z próby, a górna krawędź pudełka jest trzecim kwartlem z próby.
Mediana definiowana jest dwojako:
- Jako kwantyl rzędu 0.5
- Jako wartość środkowa w próbie uporządkowanej od wartości najmniejszych do największych (w próbie o parzystej liczbie elementów jest średnią dwóch wartości najbliższych środkowi)
Pierwsza definicja dotyczy rozkładu, nadrzędnej charakterystyki populacji statystycznej z której losuje się próby (i uważa się, że rzeczywiste dane także są efektem losowego rozkładu wartości między obiekty biologiczne). Druga definicja to mediana z próby – zgrubne, ale najlepsze z możliwych oszacowanie mediany wg pierwszej definicji.
W podobny sposób definiowane są kwartyle.
- Pierwszy kwartyl to kwantyl rzędu 0.25, trzeci kwartyl to kwantyl rzędu 0.75.
- Pierwszy kwartl z próby to wartość oddzielająca 1/4 najmniejszych wartości od pozostałych, a trzeci kwartyl z próby to wartość oddzielająca 3/4 wartości od pozostałych, w próbie uporządkowanej od wartości najmniejszych do największych.
W obu definicjach pojawiają się kwantyle pewnego rzędu. To termin statystyczny odnoszący się do nieskończonych rozkładów liczbowych. Dla skończonego ciągu a1,a2,…an kwantyl rzędu p wylicza się jako liczbę q taką, że liczba danych spośród a1,a2,…an mniejszych od q podzielona przez n jest jak najbliższa liczbie p. Na ogół liczb takich jest nieskończenie wiele i obejmują pewien odcinek (ai,aj). Kwantyl ustalany jest jako liczba (1-λ)ai+λaj dla pewnej liczby λ z przedziału [0,1]. W R wyróżnia się 9 metod wylicznia tego parametru, o czym można przeczytać w opisie funkcji quantile() wyliczającej kwantyl rzedu p dla dowolnego wektora. Wystarczy wpisać do konsoli ?quantile lub help(quantile). Domyślnie zastosowany jest typ siódmy o dość złożonym wzorze i ten kwantyl jest stosowany przez funkcję boxplot() .
Wykres pudełkowy dla średniej
Mediany i kwartyle są popularną charakterystyką danych uzyskanych w badaniach medycznych. W biologii stosuje się ją dla małych prób lub dla bardzo skośnych i nieregularnych rozkładów. Znacznie jednak częściej używa się średnich i odchyleń standardowych z próby. Są one najlepszym oszacowaniem wartości oczekiwanej i odchylenia standardowego – charakterystyk rozkładu, z którego pochodzi nasza próba danych.
Wykres pudełkowy dla średniej i odchylenia standardowego z próby uzyskamy także za pomocą funkcji boxplot() wykorzystując własność, że w pięcioelementowym uporządkowanym wektorze (x1, x2, x3, x4, x5) wartością minimalną jest x1, x2 jest pierwszym kwartylem z próby, x3 jest medianą, x4 jest trzecim kwartylem, a x5 jest wartością maksymalną. Najczęściej wystarczy zatem zrobić boxplot() dla wektora:
(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x))aby uzyskać wykres pudełkowy ze średnią i odchyleniem standardowym. Porównanie obu boxplotów (dla mediany i dla średniej) pokazuje następujący program:
x=c(13.75,7.20,7.39,0.60,12.55, 9.18, 9.21, 14.51, 11.08, 5.57, 10.88, 13.31,
11.47, 9.79, 4.64, 9.85, 12.63, 9.91, 10.23, 6.44, 2.00, 4.73, 13.63, 9.76,
17.93, 7.08, 14.32, 11.21, 10.10, 12.03, 10.43, 9.41, 7.12, 10.75, 10.79,
8.73, 11.53, 12.20, 12.36, 13.88, 10.59, 13.49, 9.57, 10.20, 9.44, 12.76,
11.51, 6.96, 3.90, 13.54, 7.32, 11.16, 12.15, 9.55, 4.50, 4.38, 11.13, 13.07,
7.49, 16.59, 4.40, 8.69, 7.13, 8.61, 8.74, 13.14, 9.60, 6.98, 8.38, 8.96,
11.98, 8.30, 11.26, 8.86, 16.08, 11.36, 6.53, 12.34, 8.76, 14.45, 16.08, 8.43,
11.49, 9.42, 10.66, 12.56, 12.51, 17.82, 8.86, 13.14, 9.74, 7.86, 13.26,
11.17, 10.93, 7.95, 6.16, 6.22, 10.17, 9.84)
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(x, range=0, xlab="", ylab="x", col="blue")
title("Mediana i odchylenia ćwiartkowe", cex.main=1, font.main=1)
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(c(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x)), range=0,
xlab="", ylab="x", col="blue")
title("Średnia i odchylenia standardowe", cex.main=1, font.main=1)
|
W obszarze od x1=średnia – odchylenie standardowe do x2=średnia + odchylenie standardowe, mieści się w przybliżeniu 70% danych. Stąd pudełka dla takich charakterystyk rozkładu są dłuższe.
Pokazana procedura nie sprawdza się, gdy w próbie są dane tak bardzo odbiegających innych wartości, że mean(x)-sd(x) jest mniejsze od min(x) lub mean(x)+sd(x) jest większe od max(x). Wtedy funkcja boxplot() zastosowana na wektorze (min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x) ) nie rysuje tego, co trzeba. Aby wykonać poprawne wykresy należy zmodyfikować wartości kryjące się pod min(x) i max(x)
x=c(1.03, 31.49, 18.49, 22.23, 32.96, 26.48, 31.58, 21.26, 24.64, 234.69)
y=c(219.97, 220.35, 218.44, 251.17, 2.00, 215.33, 215.36)
xs=c(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x))
ys=c(min(y), mean(y)-sd(y), mean(y), mean(y)+sd(y), max(y))
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(xs, ys, range=0, xlab="", ylab="x", col="blue")
title("Średnia i odchylenia standardowe ?", cex.main=1, font.main=1)
#
if (xs[2]<xs[1]) xs[1]=xs[2]
if (xs[4]>xs[5]) xs[5]=xs[4]
if (ys[2]<ys[1]) ys[1]=ys[2]
if (ys[4]>ys[5]) ys[5]=ys[4]
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(xs, ys, range=0, xlab="", ylab="x", col="blue")
title("Średnia i odchylenia standardowe", cex.main=1, font.main=1)
|
Program wygenerował dwa wykresy:
Drugi wykres, może niezbyt elegancki ze względu na ogromne odchylenia standardowe i dolną część pierwszego pudełka umieszczającą w obrębie liczb ujemnych, jest poprawny. W praktyce, przy analizie prób z wartościami znacznie odbiegającymi od pozostałych często opisuje się je osobno, a tabele, wykresy i analizy statystyczne wykonuje się dla pozostałych danych.
Test chemotaksji dla Caenorhabditis elegans, zastosowanie mediany
Nicień Caenorhabditis elegans należy do organizmów modelowych, na którym wykonuje się szereg badań fizjologicznych, między innymi bada przesyłanie sygnałów między neuronami. Poprzez stosowanie różnych substancji chemicznych można neurony blokować lub wywoływać błędy w przepływie impulsów nerwowych. Jednym ze sposobów wykazania, że jakaś substancja zmienia przepływ sygnałów między neuronami, jest test chemotaksji.
Test ten polega na umieszczenie w jednym końcu szalki petriego substancji wabiącej nicienie, w drugim końcu wypuszcza się nicienie w ilości około 100 osobników. Eksperyment wykonuje się jednocześnie na dwóch szalkach dla grupy testowej nicieni potraktowanych uprzednio substancją chemiczną i dla grupy kontrolnej. Po 60 minutach sprawdza się ile nicieni dotarło do obszaru, gdzie wylano substancję wabiącą.
Liczby nicieni |
Grupa kontrolna |
Grupa testowa |
w obszarze substancji wabiącej |
Mc | Mt |
wszystkich wypuszczonych |
Nc | Nt |
Następnie wylicza się indeks chemotaksji w postaci Mc/Nc-Mt/Nt bądź (Mc/Nc-Mt/Nt)*100%. Gdy jakaś substancja istotnie blokuje neurony nicienia, indeks ten jest dodatni i bliski jedynce.
Najczęściej tego typu eksperyment powtarza się wielokrotnie i porównuje ze sobą wyniki uzyskane dla różnych dawek substancji czynnej, w różnych temperaturach itp. Przykładem takich badań było stosowanie czterech dawek anestetyku – azydku sodu NAN3, którymi potraktowano najpierw nicienie, a następnie wykonano na nich test chemotaksji. Dla każdej dawki oraz dla kontroli test ten powtórzono 6-krotnie. Uzyskano następujące wyniki (liczby nicieni, które po godzinie dotarły do substancji wabiącej oraz liczby wszystkich nicieni na szalce), co zapisano w postaci K/N:
| Powtórzenie | Kontrola | 0.1 | 0.5 | 1 | 5 |
|---|---|---|---|---|---|
1 |
98/101 |
93/102 |
87/102 |
26/98 |
5/103 |
2 |
95/98 |
88/104 |
78/101 |
32/93 |
11/107 |
3 |
76/96 |
75/99 |
47/99 |
15/98 |
4/96 |
4 |
45/96 |
30/98 |
12/93 |
3/101 |
1/100 |
5 |
83/97 |
85/103 |
55/92 |
9/94 |
0/96 |
6 |
94/94 |
97/99 |
86/103 |
33/104 |
16/107 |
Dane takie powinny być najpierw zaimportowane do R w postaci bazy danych o kolumnach: Powtórzenie, Dawka, Liczba wypuszczonych nicieni (N), liczba nicieni w obszarze substancji wabiącej (K). Nazwom tym nadano stosowne skróty i utworzono następującą ramkę danych:
K0=c(98,95,76,45,83,94)
N0=c(101,98,96,96,97,94)
K0.1=c(93,88,75,30,85,97)
N0.1=c(102,104,99,98,103,99)
K0.5=c(87,78,47,12,55,86)
N0.5=c(102,101,99,93,92,103)
K1=c(26,32,15,3,9,33)
N1=c(98,93,98,101,94,104)
K5=c(5,11,4,1,0,16)
N5=c(103,107,96,100,96,107)
baza=data.frame(POWT=rep(1:6,5),
DAWKA=c(rep(0,6),rep(0.1,6),rep(0.5,6),rep(1,6),rep(5,6)),
N=c(N0,N0.1,N0.5, N1, N5), K=c(K0, K0.1, K0.5, K1, K5))
|
W teorii statystycznej nikt nie poleca wyliczanie średniej z procentów. Wynika to stąd ze procent wyliczony na dużej próbie jest bardziej wiarygodny od procentu wyliczonego na małej próbie. Gdybyśmy chcieli narysować procent nicieni, które dotarły do substancji wabiącej, musielibyśmy dla każdej dawki zsumować liczby nicieni ze wszystkich powtórzeń (zarówno wszystkich jak i tych, które dotarły do celu) i wyliczyć stosowny procent. Taki procent zazwyczaj pokazuje się w postaci słupków. Jego wykonanie wyglądałoby następująco:
agN=aggregate(N~DAWKA, baza, sum)
agK=aggregate(K~DAWKA, baza, sum)
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
barplot(agK[,2]/agN[,2]*100, names.arg=agN[,1],
ylim=c(0,100),
xlab="Dawki azydku sodu", ylab="Procent", col="lightgreen")
|
Program ten utworzy następujący wykres:
W przypadku testu chemotaksji wypuszcza się na szalki duże i zbliżone do siebie liczby nicieni (ich dokładną liczbę określa się dopiero po zakończeniu eksperymentu) i znacznie ważniejsze od zróżnicowania liczby wypuszczonych nicieni, wydają się zmiany warunków wykonywania powtórzeń eksperymentu (często robi się to w kolejnych dniach, albo rzadziej, przy nieco innej temperaturze, oświetleniu itp.) i zmiany jakie w tym czasie zaszły w populacji, na której wykonuje się eksperyment. Standardowo wylicza się współczynnik chemotaksji dla każdego powtórzenia osobno, a uzyskane wyniki charakteryzuje się medianą i odchyleniami ćwiartkowymi. Ostatnio standardem stało się zaznaczanie na wykresach danych (zazwyczaj jest mniej niż 20) w postaci punktów, przy czym, aby nie pokrywały się one ze sobą, daje się im losową pierwszą współrzędną, nie mniej bliską środkowi pudełka, na którym są zaznaczane. Przygotowanie danych i wykonanie wykresu wygląda następująco:
P0=baza[baza$DAWKA==0,4]/baza[baza$DAWKA==0,3]
ChemTax0.1=P0 - baza[baza$DAWKA==0.1,4]/baza[baza$DAWKA==0.1,3]
ChemTax0.5=P0 - baza[baza$DAWKA==0.5,4]/baza[baza$DAWKA==0.5,3]
ChemTax1=P0 - baza[baza$DAWKA==1,4]/baza[baza$DAWKA==1,3]
ChemTax5=P0 - baza[baza$DAWKA==5,4]/baza[baza$DAWKA==5,3]
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(ChemTax0.1, ChemTax0.5, ChemTax1, ChemTax5,
range=0, names=paste(c(0.1, 0.5, 1, 5)),
xlab="Dawka azydku sodu", ylab="Wsp. chemitaksji", col="lightgreen")
points(rnorm(6,1,0.05), ChemTax0.1, pch=19, col="red")
points(rnorm(6,2,0.05), ChemTax0.5, pch=19, col="red")
points(rnorm(6,3,0.05), ChemTax1, pch=19, col="red")
points(rnorm(6,4,0.05), ChemTax5, pch=19, col="red")
|
Wykres utworzony przez ten program wygląda następująco:
Ze względu na element losowy stosowany przy ustalaniu współrzędnej poziomej czerwonych punktów, powtórzenie kodu rysowania wykresu spowoduje powstanie nieco innego ułożenia czerwonych kropek. Należy wybrać taki wykres, w którym można doliczyć się na pasie każdego pudełka 6 różnych punktów. Tego typu wykresy są standardem przy pokazywaniu indeksu chemotaksji uzyskanego eksperymentalnie.
Długość i szerokość płatków okwiatu i działek kielicha trzech gatunków irysów, obrazowanie średnich
W zaimplementowanej do R bazie iris pokazano wyniki pomiarów długości i szerokości płatków okwiatu i płatków kielicha trzech gatunków irysów. Typowym sposobem zobrazowania tych wyników są pudełka ze średnimi i odchyleniami standardowymi wyników pomiarów. Tych zmiennych ciągłych jest cztery. Ich nazwy i numer kolumny, w której są umiejscowione, najlepiej jest uzyskać stosując funkcję str(iris).
> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
|
Aby zastosować funkcję graficzną boxplot() do uzyskania stosownych wykresów należy wyliczyć dla każdej zmiennej ciągłej, dla każdego gatunku irysa wielkości: wartość minimalną (funkcja min()), średnią minus odchylenie standardowe (mean()-sd()), średnią (mean()), średnia plus odchylenie standardowe (mean()+sd()), oraz wartość maksymalną (funkcja max()). Wyliczanie tych wielkości można skrócić stosując pętle i funkcję aggregate(). Pętlę można zastosować robiąc obliczenia dla wszystkich kolumn dla których rysujemy wykres pudełkowy. W bazie iris wykorzystano fakt, że zmienne ciągłe zajmują cztery pierwsze kolumny bazy danych. Gdy zdarzy się, że zmienne, dla których zastosować pętle, zajmują kolumny 2, 4, 6 i 7, możemy także stosować pętlę w postaci for (i in c(2,4,6:7)) {}. Funkcję aggregate() natomiast stosujemy, by uzyskać odpowiednie wartości od razu dla trzech gatunków irysów.
Uzyskanie odpowiednich wartości do zrobienia czterech wykresów pudełkowych z trzema pudełkami na każdym, może wyglądać następująco:
#Wyliczanie min(), mean()-sd(), mean(), mean()+sd() i max()
#dla 4 różnych zmiennych ciagłych.
MIN=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, min)[,2]->x
MIN=cbind(MIN,x)}
names(MIN)[2:5]=names(iris)[1:4]
MEAN.minus.SD=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris,
function(x) mean(x)-sd(x))[,2]->x
MEAN.minus.SD=cbind(MEAN.minus.SD,x)}
names(MEAN.minus.SD)[2:5]=names(iris)[1:4]
MEAN=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, mean)[,2]->x
MEAN=cbind(MEAN,x)}
names(MEAN)[2:5]=names(iris)[1:4]
MEAN.plus.SD=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris,
function(x) mean(x)+sd(x))[,2]->x
MEAN.plus.SD=cbind(MEAN.plus.SD,x)}
names(MEAN.plus.SD)[2:5]=names(iris)[1:4]
MAX=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, max)[,2]->x
MAX=cbind(MAX,x)}
n#ames(MAX)[2:5]=names(iris)[1:4]
#Poprawki na przypadek,
#gdy mean-sd<min lub mean+sd>max
for (i in 1:3) for (j in 2:5) if (MIN[i,j]>MEAN.minus.SD[i,j]){
MIN[i,j]=MEAN.minus.SD[i,j]}
for (i in 1:3) for (j in 2:5) if (MAX[i,j]<MEAN.plus.SD[i,j]){
MAX[i,j]=MEAN.plus.SD[i,j]}
#Połaczenie wyników w jedną bazę
iris_1=rbind(MIN,MEAN.minus.SD,MEAN,MEAN.plus.SD,MAX)
|
Narysowanie od razu czterech wykresów także można wykonać w pętli:
#Rysowanie 4 wykresów
kolory=c("green","green","orange","orange")
for (i in 2:5) {
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(iris_1[,i]~Species, iris_1, xlab="Species", ylab=names(iris_1)[i],
col=kolory[i-1])}
|
Program tworzy cztery następujące wykresy:
Jak można się domyślić, zielone pudełka dotyczą wymiarów działek kielicha, a pomarańczowe – płatków okwiatu.
Stężenie fluoru w wydzielinie gruczołów odbytowych skunksów, mediany i średnie
Pokazanie na jednym wykresie zarówno median jak i średnich tych samych danych jest informacją o skośności rozkładu (gdy mediany znacznie różnią się od średnich) lub o jej braku (gdy obie te charakterystyki prawie się pokrywają). Wielkościom tym powinny towarzyszyć odchylenia ćwiartkowe i standardowe, gdyż tylko wtedy można ocenić wielkość różnicy między medianą a średnią. To dodatkowo pokazuje w jakim zakresie mieści się połowa danych najbliższych medianie i 70% danych najbliższych średniej. Jest to masa dodatkowych informacji charakteryzujących rozkłady danych i warto takie wykresy wykonać. Pozwala to sprawdzić, czy wnoszą one coś nowego do interpretacji danych, czy raczej ją utrudniają.
Obrazowanie zarówno średnich z odchyleniami standardowymi jak i median z odchyleniami ćwiartkowymi na jednym wykresie polega na narysowaniu jednej charakterystyki w postaci pudełka a drugiej w innej formie (najczęściej punktu z odchyleniami w postaci strzałek) nałożonej na to pudełko.
Wykonanie tego typu wykresów pokazano na przykładzie bazy danych dotyczących badań stężenia fluoru w wydzielinie gruczołów odbytowych skunksów, która pokazywana jest na ćwiczeniach z informatyki studentów biologii UW. Baza ta została zaprezentowana w pierwszej części tego podręcznika “R dla biologów, podstawowe operacje” w rozdziale o ramkach danych w podrozdziale “Operacje wykonywane na ramkach danych”.
Zobrazowanie median z odchyleniami ćwiartkowymi w postaci pudełka i średnich z odchyleniami standardowymi w postaci punktów ze strzałkami na jednym wykresie wygląda następująco:
skunks$SEZON=ordered(skunks$SEZON, levels=c("wiosna", "jesień", "zima"))
#
windows(4.5, 2.5)
#
par( mar=c(3,3,0.5,4.5), mgp=c(1.8,0.5,0), las=1, xpd=TRUE, ps=12)
#
boxplot(FLUOR ~ SEZON+PLEC, skunks,
col=c("green", "gold", "lightblue"),
names=c(" ", "samice"," ", " ", "samce", " "),
xlab="Płeć osobników",
ylab=expression("Stężenie fluoru [ "* ng %.% g^-1 *"]"))
#
lines(c(1,3),c(21,21))
lines(c(4,6),c(21,21))
#
legend(6.5, 40,
title="sezon",
legend=c("wiosna", "jesień", "zima"),
fill=c("green", "gold", "lightblue"),
box.col="white")
#
sr = aggregate(FLUOR ~ SEZON+PLEC, skunks, mean)
odsd = aggregate(FLUOR ~ SEZON+PLEC, skunks, sd)
xi = 1:6+0.1
points(xi, sr$FLUOR, col = grey(0.2), pch = 15)
arrows(xi, sr$FLUOR - odsd$FLUOR, xi, sr$FLUOR + odsd$FLUOR, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
#
x1=6.8
x2=7
y1=25
y2=27
rect(x1,y1,x2,y2)
lines(c((x1+x2)/2,(x1+x2)/2),c(y1-1,y2+1), lty=2)
lines(c(x1,x2),c(y1+0.5,y1+0.5),lwd=2)
lines(c(x1,x2),c(y1-1,y1-1))
lines(c(x1,x2),c(y2+1,y2+1))
text(x2+0.3,(y1+y2)/2,"mediana\ni odch.\nćwiart.", adj=0)
#
x1=(x1+x2)/2
y1=20
points(x1, y1, col = grey(0.2), pch = 15)
arrows(x1, y1-2, x1, y1 + 2, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
text(x1+0.4,y1,"średnia\ni odch.\nstand.", adj=0)
|
Po wykonaniu tego programu w R uzyskujemy następujący wykres:
Zobrazowanie średnich z odchyleniami standardowymi w postaci pudełka i median z odchyleniami ćwiartkowymi w postaci punktów ze strzałkami na jednym wykresie wygląda następująco:
skunks$SEZON=ordered(skunks$SEZON, levels=c("wiosna", "jesień", "zima"))
#
# zrobienie wykresów pudełkowych ze średnią i odch. standardowymi.
Min=aggregate(FLUOR ~ SEZON+PLEC, skunks, min)
Sr.minus.sd = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) mean(x)-sd(x))
Sr = aggregate(FLUOR ~ SEZON+PLEC, skunks, mean)
Sr.plus.sd = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) mean(x)+sd(x))
Max = aggregate(FLUOR ~ SEZON+PLEC, skunks, max)
#
# Poprawki na ewentualność Sr.minus.sd<min i Sr.plus.sd>max
for (i in 1:6) if (Min[i,3]>Sr.minus.sd[i,3]) Min[i,3]=Sr.minus.sd[i,3]
for (i in 1:6) if (Max[i,3]<Sr.plus.sd[i,3]) Max[i,3]=Sr.plus.sd[i,3]
#
# Połączenie podbaz
skunks_1=rbind(Min, Sr.minus.sd, Sr, Sr.plus.sd, Max)
#
windows(4.5, 2.5)
par( mar=c(3,3,0.5,4.5), mgp=c(1.8,0.5,0), las=1, xpd=TRUE, ps=12)
#
boxplot(FLUOR ~ SEZON+PLEC, skunks_1,
col=c("#80FF80FF", "#FF8080FF", "#8080FFFF"),
names=c(" ", "samice"," ", " ", "samce", " "),
xlab="Płeć osobników",
ylab=expression("Stężenie fluoru [ "* ng %.% g^-1 *"]"))
#
lines(c(1,3),c(21,21))
lines(c(4,6),c(21,21))
#
legend(6.5, 40,
title="sezon",
legend=c("wiosna", "jesień", "zima"),
fill=c("#80FF80FF", "#FF8080FF", "#8080FFFF"),
bty="n")
#
# Naniesienie median z odchyleniami ćwiartkowymi.
#
Med = aggregate(FLUOR ~ SEZON+PLEC, skunks, median)
Cw0.25 = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) quantile(x,0.25))
Cw0.75 = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) quantile(x,0.75))
xi = 1:6
points(xi, Med$FLUOR, col = "white", pch = 15)
arrows(xi, Cw0.25$FLUOR, xi, Cw0.75$FLUOR, code = 3,
col = "white", lwd=2, angle = 45, length = 0.1)
#
x1=6.8
x2=7
y1=25
y2=27
rect(x1,y1,x2,y2)
lines(c((x1+x2)/2,(x1+x2)/2),c(y1-1,y2+1), lty=2)
lines(c(x1,x2),c((y1+y2)/2,(y1+y2)/2),lwd=2)
lines(c(x1,x2),c(y1-1,y1-1))
lines(c(x1,x2),c(y2+1,y2+1))
text(x2+0.3,(y1+y2)/2,"średnia\ni odch.\nstand.", adj=0)
#
x1=(x1+x2)/2
y1=20
points(x1, y1, col = grey(0.2), pch = 15)
arrows(x1, y1-3, x1, y1 + 2, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
text(x1+0.4,y1,"mediana\ni odch.\nćwiart.", adj=0)
|
Po wykonaniu pierwszej części tego programu uzyskamy pierwszy wykres, a wykonanie całości – drugi wykres:
Wykres pierwszy jest standardem obrazowania zależności zmiennej ciągłej od zmiennej dyskretnej.
Wykresy liniowe, zastosowanie
Wszelkie procesy czasozależne (dobowe zmiany temperatury, miesięczne zmiany średniej temperatury dobowej, roczne zmiany średniej temperatury miesięcznej, dynamiki liczebności, zagęszczenia populacji itd) oraz ogólnie zmiany zmiennej Y względem uporządkowanej zmiennej X pokazuje się na wykresach liniowych. Zobrazowanie kolejnych danych uzyskanych w czasie badań, jako punktów połączonych kreskami, wyraźnie pokazuje uporządkowanie zmiennej niezależnej. Wykres typu:
ma sens tylko wtedy, gdy omawia się gradient jakiś zjawisk na transekcie południe -> północ. Wykres ten został uzyskany za pomocą programu:
windows(4.5, 2.5)
par(mar=c(3,2.5,1,1),mgp=c(1.5,0.5,0))
plot(1:3,c(33.7, 48.2, 96.0), typ="b", axes=FALSE, xlim=c(0.5,3.5),
xlab="Park Narodowy", ylab="")
box()
axis(1, 1:3, labels=c("Bieszczacki", "Poleski", "Białowieski"))
axis(2)
|
Dynamiki liczebności drobnych ssaków
Podstawowe zagadnienia obrazuje się najczęściej za pomocą wielu linii – każda zależna od tej samej zmiennej X i obliczona dla innej kategorii danych, np. dynamika liczebności wyliczona dla innego gatunku drobnych gryzoni leśnych. Jeżeli liczebności tych gatunków zmieniały się w czasie sezonu badawczego zgodnie z następująca tabelą:
| Miesiąc | Mysz leśna | Mysz polna | Nornica ruda |
|---|---|---|---|
Mar |
12 |
27 |
3 |
Kwi |
10 |
32 |
4 |
Maj |
22 |
29 |
17 |
Cze |
43 |
54 |
25 |
Lip |
38 |
88 |
30 |
Sie |
51 |
76 |
62 |
Wrz |
85 |
101 |
70 |
Paz |
75 |
65 |
43 |
Lis |
73 |
54 |
20 |
to odpowiedni liniowy wykres ich dynamik liczebności uzyskamy za pomocą programu:
Sezon=c("Mar", "Kwi", "Maj", "Cze", "Lip", "Sie", "Wrz", "Paz", "Lis")
AF=c(12,10,22,43,38,51,85,75,73)
AA=c(27,32,29,54,88,76,101,65,54)
MG=c(3,4,17,25,30,62,70,43,20)
windows(4.5, 2.5)
par(mar=c(3.5,3.5,0.1,0.1), mgp=c(1.8, 0.5, 0))
matplot(1:9, cbind(AF, AA, MG), typ="l",
lty=c(1,2,3), lwd=c(1,2,3),
col=c("green2","red","blue"), axes=FALSE,
xlab="Miesiące", ylab="Liczba osobników" )
axis(1,1:9,Sezon)
axis(2)
legend(0.5,110,lwd=c(1,2,3),lty=c(1,2,3),col=c("green2","red","blue"),
legend=c("AF", "AA", "MG"),bty="n")
|
Będzie on wyglądał następująco:
Wykresy punktowe, scatterplot
Stosowanie wykresów punktowych
Pojęcie “wykres punktowy” lub “scateterplot” (słowo coraz częściej używane w języku polskim) oznacza, że pewne dane zostały zaznaczone na wykresie w postaci punktowych znaczników – kółeczek, kwadracików, trójkątów, kresek lub innych wzorów, a także, choć rzadko liter lub cyferek. W taki sposób wykreśla się dane, gdy nie ma powodu by łączyć je kreskami. Najczęściej wykresami punktowymi obrazuje się zależność między dwoma zmiennymi liczbowymi. Bardzo często obiekty podlegają więcej niż dwóm pomiarom i odpowiedni “wykres” punktowy istnieje w przestrzeni wielowymiarowej. Dla trzywymiarowych wykresów można utworzyć wykres przestrzenny i wykonać jego rzut na płaszczyznę dwuwymiarową. Dla wielowymiarowych danych coraz częściej w literaturze biologicznej pojawiają się biploty – wykresy na których poszczególne zmienne zaznaczone są strzałkami, a obiekty punktami, których współrzędne nic nie znaczą (ważne jest ich rozmieszczenie względem strzałek). Ich tworzenie, interpretacja i ogólnie “czytanie” wymaga dość zmatematyzowanej teorii i zostaną one omówione później.
Gdy mamy dwa pomiary tego samego obiektu wykonanego dla dużej liczby osobników i chcemy wykonać rozrzut punktów na odpowiednim wykresie, należy dobrze zastanowić się, którą zmienną umieścimy na osi 0X, a którą na osi 0Y. Oznacza przemyślenie następującego problemu: czy zmienna pierwsza wpływa na drugą czy raczej druga na pierwszą. Mówimy tu o wpływie rozumianym jako istnienie jakichkolwiek procesów biofizycznych lub biochemicznych, które kształtowałyby w jakiś sposób wartości jednej zmiennej przy zmianach wartości drugiej zmiennej. Mówimy o zależności przyczynowo-skutkowej zmiennych od siebie.
Gdy możemy wyróżnić zmienną niezależną i zależną (a często wcale nie jest to trudne) to wartości zmiennej niezależnej umieszcza na osi poziomej, a wartości zmiennej zależnej na osi pionowej. Istnieją jednak w biologii zmienne, które bezpośrednio na siebie nie wpływają, ale ich wartości mogą zależeć od innej, nie badanej z różnych powodów, zmiennej. Wtedy w zasadzie wszystko jedno którą zmienną umieścimy na osi poziomej, a którą na osi pionowej. Zasady te obrazuje poniższy diagram:
W biologii nie ma zmiennych, które zupełnie, ani bezpośrednio ani pośrednio, niezależą od siebie. Tylko czasem ta zależność jest bardzo pośrednia i tak nikła, że można ją pominąć. Zależność i niezależność zmiennych omawiana na statystyce oznacza inne, czysto matematyczne zjawisko i tylko przez przypadek nazywa się ją tym samym słowem. Ta statystyczna zależność nie ma żadnego znaczenia, jeżli chodzi o umiejscawianie zmiennych na wykresie.
Czas przeprowadzenia badań terenowych będzie na osi 0X, a liczebność populacji w tym czasie na osi 0Y. Przy odwrotnym układzie sugerowalibyśmy, że liczebność populacji wpływa na upływ czasu. Czas jest zawsze zmienną niezależną dla wszelkich pomiarów, które zmieniają się w czasie, choć nazwanie tu zależności przyczynowo-skutkowej może być problematyczne (pewnie ze względu na jej oczywistość). Ale czy cokolwiek, co mierzymy w biologii wpływa na upływ czasu? Na ogół zmiennymi niezależnymi są wszelkie czynniki abiotyczne, jak: temperatura powietrza, wilgotność, długość dnia, odległość od szosy itd. a zależnymi wszelkie pomiary biotopu. Podobnie stężenie ołowiu w osadach dennych w różnych fragmentach jeziora będzie na osi 0X, a stężenie ołowiu w planktonie pobranym z tych fragmentów na osi 0Y. Tu już zależność nie jest na 100% oczywista, bo to obumierający plankton mógłby zanieczyszczać osady. Nie mniej, wymagałoby podtruwania planktonu z pominięciem zatruwania abiotycznych elementów jeziora, a to raczej się nie zdarza.
Bywa jednak że wyznaczenie zmiennej niezależnej i zależnej nie jest możliwe. Czy wzrost wpływa na ciężar, czy ciężar na wzrost? Obie zmienne kształtują się w okresie wzrostu osobników przez te same czynniki. Podobnie stężenia wielu zanieczyszczeń we krwi (wątrobie, nerkach, tłuszczu itd…) różnych organizmów tworzą dane, dla których bezpośredni wpływ na siebie raczej nie istnieje. Zależą one od tego, z jak bardzo zanieczyszczonego środowiska pochodzą organizmy, a z reguły środowiska zanieczyszczone są wieloma toksykantami jednocześnie.
Rozprawa o parkach narodowych w Polsce
W rozprawie o okresach politycznych w dziejach Polski najbardziej sprzyjających ochronie przyrody autor chce zamieścić wykres pokazujący zależność między czasem powstania parku narodowego, a jego powierzchnią. Dane do tego wykresu pobrał z Wikipedii.
Nazwa |
Rok powstania |
Powierzchnia [km2] |
Liczba odwiedzających rocznie |
Babiogórski Park Narodowy |
1954 |
33.9 |
60000 |
Białowieski Park Narodowy |
1932 |
105.17 |
140000 |
Biebrzański Park Narodowy |
1993 |
592.23 |
54000 |
Bieszczadzki Park Narodowy |
1973 |
291.96 |
200000 |
Park Narodowy Bory Tucholskie |
1996 |
46.13 |
60000 |
Drawieński Park Narodowy |
1990 |
113.42 |
25000 |
Gorczański Park Narodowy |
1981 |
70.3 |
45000 |
Park Narodowy Gór Stołowych |
1993 |
63.4 |
360000 |
Kampinoski Park Narodowy |
1959 |
385.48 |
1000000 |
Karkonoski Park Narodowy |
1959 |
55.8 |
2000000 |
Magurski Park Narodowy |
1995 |
194.39 |
40000 |
Narwiański Park Narodowy |
1996 |
68.1 |
5000 |
Ojcowski Park Narodowy |
1956 |
21.46 |
400000 |
Pieniński Park Narodowy |
1932 |
23.46 |
585000 |
Poleski Park Narodowy |
1990 |
97.62 |
9000 |
Roztoczański Park Narodowy |
1974 |
84.82 |
100000 |
Słowiński Park Narodowy |
1967 |
215.72 |
282000 |
Świętokrzyski Park Narodowy |
1950 |
76.26 |
400000 |
Tatrzański Park Narodowy |
1954 |
211.87 |
2500000 |
Park Narodowy Ujście Warty |
2001 |
80.74 |
10000 |
Wielkopolski Park Narodowy |
1957 |
75.83 |
? |
Wigierski Park Narodowy |
1989 |
149.99 |
120000 |
Woliński Park Narodowy |
1960 |
109.37 |
1500000 |
Odpowiednie dane łatwo z tabeli przenieść do skryptu w postaci dwóch ciągów:
x=c(1954, 1932, 1993, 1973, 1996, 1990, 1981, 1993, 1959, 1959, 1995, 1996, 1956,
1932, 1990, 1974, 1967, 1950, 1954, 2001, 1957, 1989, 1960)
y=c(33.9, 105.17, 592.23, 291.96, 46.13, 113.42, 70.3, 63.4, 385.48, 55.8,
194.39, 68.1, 21.46, 23.46, 97.62, 84.82, 215.72, 76.26, 211.87, 80.74,
75.83, 149.99, 109.37)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), xaxs="i", yaxs="i")
plot(x,y,col="green3", pch=19, xlab="Rok powstania parku narodowego",
ylab=expression("Pwierzchnia [ " * km^2 * "]"),
xlim=c(1930, 2010), ylim=c(0,600), axes=FALSE)
axis(1,at=193:210*10, labels=193:210*10)
axis(2, at=0:6*100, labels=c("0","","200","","400","","600"))
|
Utworzony wykres spełnia wszystkie oczekiwania.
W wykresach tego typu zastosowano opcje funkcji par(): xaxs=”i” i yaxs=”i”. Powodują one, że punkt przecięcia się osi wypada zawsze w (xlim[1],ylim[1]). Należy jednak wtedy pamiętać o opcjach xlim i ylim funkcji plot(), by pole kreślenia nie zaczynało się dla najmniejszych wartości ciągów x i y, a kończyło dla największych.
Liczba turystów odwiedzających rocznie dany park pokazuje jego społeczno-edukacyjną rolę, a jednocześnie pewne zagrożenie dla chronionej przyrody zwłaszcza gdy park ma małą powierzchnię. Liczba ta wydaje się nie mieć żadnego związku z rokiem założenia parku oraz z jego powierzchnią. Można to uwidocznić na wykresie pokazującym, jak liczba odwiedzających park narodowy zależy od roku jego założenia, w którym kółeczko oznaczające zależność będzie miało powierzchnię proporcjonalną do powierzchni parku narodowego.
x=c(1954, 1932, 1993, 1973, 1996, 1990, 1981, 1993, 1959, 1959, 1995, 1996, 1956,
1932, 1990, 1974, 1967, 1950, 1954, 2001, 1957, 1989, 1960)
y=c(33.9, 105.17, 592.23, 291.96, 46.13, 113.42, 70.3, 63.4, 385.48, 55.8,
194.39, 68.1, 21.46, 23.46, 97.62, 84.82, 215.72, 76.26, 211.87, 80.74, 75.83,
149.99, 109.37)
z=c(60000, 140000, 54000, 200000, 60000, 25000, 45000, 360000, 1000000,
2000000, 40000, 5000, 400000, 585000, 9000, 100000, 282000, 400000,
2500000, 10000, NA, 120000, 1500000)
#
windows(4.5, 2.5)
par(mar=c(3,4,1,1), mgp=c(1.7, 0.5, 0), xaxs="i", yaxs="i")
plot(x,z,col="green3", pch=19, cex=sqrt(y/50),
xlab="Rok powstania parku narodowego",
ylab="Liczba odwiedzających \n [tys/rok]",
xlim=c(1930, 2010), ylim=c(0,2600000), axes=FALSE)
axis(1,at=193:210*10, labels=193:210*10)
axis(2, at=0:5*500000, labels=c("0","","1000","","2000",""))
|
Powyższy kod spowodował utworzenie wykresu:
Opcja cex=c() wykorzystana do zróżnicowania wielkości znaczników, określa średnicę wykreślanego “punktu”. Aby powierzchnia znaczników była proporcjonalna do ciągu x należy pod cex= wstawić pierwiastki wartości tego ciągu.
Praca o polichlorowanych bifenylach w wątrobach dorszy z Zatoki Gdańskiej
W wątrobie dorszy złowionych w 2011 roku w Zatoce Gdańskiej oznaczono stężenia różnych pochodnych kongenerów PCB, odmian HCH (α-HCH+β-HCH+γ-HCH) i DDT (DDD+DDE+DDT). Powstała baza danych, którą można wsadzić do R i zobrazować różne zależności między zmiennymi.
dorsze = data.frame( wiek=c("5+","5+","5+","5+","5+","5+","5+","5+","5+","5+",
"5+", "5+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+",
"6+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+","6+",
"6+","6+","6+","7+","7+","7+","7+","7+","7+","7+","7+","7+","7+",
"7+"),
PCBs=c(20.00, 20.00, 20.00, 10.00, 25.00, 25.00, 25.00, 10.00,
25.00, 25.00, 25.00, 10.00, 10.00, 30.00, 35.00, 40.00, 40.00,
40.00, 40.00, 45.00, 35.00, 35.00, 10.00, 45.00, 40.00, 40.00,
40.00, 40.00, 55.00, 55.00, 55.00, 60.00, 60.00, 60.00, 50.00,
40.00, 50.00, 60.00, 60.00, 60.00, 80.00, 80.00, 90.00, 90.00,
100.00, 150.00, 200.00, 200.00, 150.00, 100.00, 200.00),
HCH=c(15.00, 15.00, 10.00, 10.00, 0.00, 5.00, 15.00, 30.00, 25.00,
10.00, 25.00, 30.00, 35.00, 35.00, 35.00, 35.00, 40.00, 35.00,
35.00, 40.00, 45.00, 45.00, 45.00, 45.00, 40.00, 35.00, 35.00,
40.00, 50.00, 60.00, 60.00, 80.00, 50.00, 40.00, 60.00, 40.00,
60.00, 80.00, 40.00, 70.00, 100.00, 80.00, 130.00, 70.00, 135.00,
70.00, 135.00, 90.00, 85.00, 65.00, 70.00),
DDT = c(35.00, 35.00, 10.00, 10.00, 10.00, 30.00, 35.00, 45.00,
10.00, 20.00, 40.00, 45.00, 60.00, 70.00, 50.00, 60.00, 60.00,
45.00, 45.00, 45.00, 70.00, 70.00, 70.00, 45.00, 70.00, 70.00,
75.00, 75.00, 95.00, 105.00, 55.00, 90.00, 100.00, 95.00, 50.00,
80.00, 105.00, 105.00, 60.00, 80.00, 115.00, 90.00, 90.00, 70.00,
110.00, 80.00, 155.00, 90.00, 160.00, 50.00, 100.00))
|
W pierwszej kolumnie wpisano przybliżoną wartość wieku złowionych dorszy określoną po ich wymiarach.
Chcąc zobrazować wzajemne związki między tymi trzema zmiennymi (czy wzrost stężenia PCBs wiąże się z większymi wartościami HCH i DDT) można wykonać trzy wykresy typu plot(). Aby zaznaczyć różnymi kolorami wiek badanych dorszy zdefiniowano funkcję kol().
kol = function(x){y=1:length(x)
for (i in 1:length(x)){ if (x[i]=="5+") y[i]="green"
if (x[i]=="6+") y[i]="blue"
if (x[i]=="7+") y[i]="red"}
y}
#
windows(2.5, 2.5)
par(mar=c(2.7,2.7,0.5,0.5), mgp=c(1.5,0.5,0))
plot(dorsze$PCBs,dorsze$HCH, pch=19,xlab="PCBs",
ylab="HCH", col=kol(dorsze$wiek))
#
windows(2.5, 2.5)
par(mar=c(2.7,2.7,0.5,0.5), mgp=c(1.5,0.5,0))
plot(dorsze$PCBs,dorsze$DDT, pch=19,xlab="PCBs",
ylab="DDT", col=kol(dorsze$wiek))
#
windows(2.5, 2.5)
par(mar=c(2.7,2.7,0.5,0.5), mgp=c(1.5,0.5,0))
plot(dorsze$HCH,dorsze$DDT, pch=19,xlab="HCH",
ylab="DDT", col=kol(dorsze$wiek))
|
Powstaną w ten sposób następujące wykresy:
Można jeszcze uznać za stosowne narysowanie zależności PCBs od HCH, PCBs od DDT i HCH od DDT, gdyż tego typu dane nie określają zmiennej zależnej i niezależnej. Powstałe wykresy byłyby odbiciem symetrycznym względem przekątnej uzyskanych wcześniej wykresów. Często w takich przypadkach tworzy się macierz wykresów, którą w R można wykonać za pomocą funkcji pairs(). Funkcja ta nie korzysta z opcji graficznych opisanych funkcją par(), ale posiada wiele własnych opcji graficznych regulujących szerokość marginesów wewnętrznych i zewnętrznych, wielkość czcionek itp. Można o nich przeczytać po wywołaniu pomocy ?pairs.
windows(5, 5)
pairs(~PCBs+HCH+DDT,data=dorsze, col=kol(dorsze$wiek), pch=19,
main="Macierz wzajemnych zależności między zmiennymi", oma=c(2,2,5,2))
|
Macierz ta wygląda następująco:
Niekiedy istnieje potrzeba zobrazowania wszystkich tych zależności na jednym trzywymiarowym wykresie. W standardowych pakietach takich możliwości nie ma. Najbardziej przejrzyste wykresy punktowe trójwymiarowe znajdują sią, jak dotąd, w pakiecie scatterplot3d. Trzeba go najpierw zainstalować. Należy wybrać z górnego menu opcje “Pakiety”, następnie “Zainstaluj pakiety” i po wybraniu kraju z serwerem CRAN wybrać pakiet scatterplot3d. Następnie można uruchomić program:
windows(4, 4)
library(scatterplot3d)
scatterplot3d(dorsze$PCBs,dorsze$HCH,dorsze$DDT, xlab="PCBs", ylab="HCH",
zlab="DDT", main="Wzajemne związki między zmiennymi")
#
windows(4, 4)
library(scatterplot3d)
scatterplot3d(dorsze$PCBs,dorsze$HCH,dorsze$DDT, xlab="PCBs", ylab="HCH",
zlab="DDT", type="h", pch=19, color=kol(dorsze$wiek),
main="Wzajemne związki między zmiennymi")
|
Drugi wykres jest taki sam jak pierwszy, tylko po zastosowaniu odpowiednich opcji w funkcji scatterplot3d(). Funkcja ta bowiem nie korzysta z opcji graficznych funkcji par().
Funkcja scatterplot3d(x,y,z) ma bardzo dużo opcji, między innymi:
- color – ciag kolorów poszczególnych punktów,
- main, sub – tytuł i podtytuł wykresu,
- xlim, ylim, zlim – zakresy wartości poszczególnych zmiennych,
- xlab, ylab, zlab – nazwy poszczególnych zmiennych,
- scale.y – skala dla zmiennej y względem zmiennych x i z
- angle – kąt miedzy zmiennymi x i y
- axis – zmienna logiczna pokazująca czy osie mają być rysowane przez funkcje scatterplot3d,
- tick.marks – zmienna logiczna wskazująca czy mają być rysowane domyślne znaczniki na osiach,
- grid – zmienna logiczna wskazująca czy na płaszczyźnie x×y ma zostać narysowana siatka,
- box – zmienna logiczna wskazująca, czy ma zostać zaznaczone pudełko, w którym zamknięte są dane,
- type – jeden ze znaków “p” (punkty), “l” (linie), “h” (pionowe odcinki) oznaczający sposób zobrazowania punktów (x,y,z),
- highlight.3d – zmienna logiczna, której wartość TRUE powoduje zróżnicowanie kolorów różnych punktów w zależności od wartości zmiennej z,
- col.axis, col.grid, col.lab – kolory osi, siatki, podpisów,
- cex.symbols, cex.axis, cex.lab – rozmiary punktów, znaczników osi, czcionki,
- font.axis, font.lab – czcionki użyte na wykresie,
- lty.axis, lty.grid, lty.hplot – typy linii użytych do wykreślenia osi, siatki, pionowych linii łączących punkty z płaszczyzną x×y.
Pozostałe opcje można znaleźć w pliku pomocy, który zostanie wgrany po wywołaniu ?scatterplot3d.
Wykresy linii trendu i prostej regresji
Regresja liniowa
Średnie, mediany, odchylenia standardowe i ćwiartkowe charakteryzują pojedyncze zmienne liczbowe. W tym rozdziale omówiona zostanie regresja charakteryzująca dane mające postać par liczb. Chodzi i o pary uporządkowane. Pierwszą liczbą może być długość osobnika, druga jego ciężarem. Regresja między długością i ciężarem jest odpowiednikiem charakterystyki centralnej rozkładu, czyli np. wartości oczekiwanej albo mediany. Korelacja (a właściwie jej kwadrat) jest odpowiednikiem odchylenia standardowego. Jeżeli zatem w pracy zdecydujemy się podawać średnie i odchylenia standardowe bez nawiasów to regresje i korelacje powinny być potraktowane tak samo.
Regresja charakteryzuje zależność zmiennych liczbowych od siebie. Zależność ta mogłaby polegać na tym, że wzrost wartości jednej zmiennej zwiększa prawdopodobieństwo, że wartości drugiej zmiennej będą się zwiększać albo zmniejszać. Niekiedy taka zależność jest bardzo dobrze widoczna, jak na poniższych wykresach punktowych.
Zależność między zmiennymi najlepiej pokazałoby nachylenie prostej najlepiej dopasowanej do narysowanych danych. Kryteria takiego dopasowania mogłyby być bardzo różnie sformułowane. Po pierwsze należałoby określić w jaki sposób mierzymy dopasowanie pojedynczego punktu do prostej. Obrazują to następujące wykresy:
| x = 1:5 y = x + rnorm(5) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,x,x) text(5,1,”dopasowanie = \nodległość w pionie \npunktu od prostej”, adj=0) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,y,y) text(5,1,”dopasowanie = \nodległość w poziomie \npunktu od prostej”, adj=0) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0)) plot(x,y,, xlim=c(0,13), ylim=c(0,6)) abline(0,1) segments(x,y,(x+y)/2,(x+y)/2) text(5,1,”dopasowanie = \nminimalna odległość \npunktu od prostej”, adj=0) |
Program ten tworzy trzy wykresy:
Po drugie, mając wiele pomiarów dopasowań pojedynczych punktów do prostej, należałoby zdecydować się na jakąś funkcję agregacyjną, by móc wyliczać dopasowanie prostej do danych, wskazywać lepiej lub gorzej dopasowane i ostatecznie wybrać prostą najlepszą. Takimi funkcjami aggregacyjnymi mogłyby być suma odległości, suma kwadratów odległości, średnia odległość i wiele innych funkcji.
Po ustaleniu reguł, dla każdej prostej y=ax+b i każdego zestawu par punktów (x1, x2 …, xn), (y1, y2, …, yn) można wyliczyć funkcję agregacyjną F((x1,x2,…,xn),(y1,y2,…,yn),ax+b). Należałoby znaleźć taką prostą (czyli takie a i b), dla której funkcja agregacyjna ma minimum. Sprowadza się do poszukiwania minimum lokalnego funkcji (a,b) → F((x1,x2,…,xn),(y1,y2,…,yn),ax+b). Wyznaczenie pochodnych cząstkowych tej funkcji dla a i b, przyrównanie ich do 0, pozwala na wyliczenie a i b, dla których funkcja agregująca ma minimum. To z kolei daje ogólny wzór na wyliczanie najlepiej dopasowanej prostej według przyjętych kryteriów do dowolnego zestawu danych.
Spośród najróżniejszych propozycji definiowania funkcji agregacyjnej najpopularniejsza jest definicja Karla Pearsona. Jest to suma kwadratów odległości. Natomiast odległości wylicza się w pionie i podnosi do kwadratu. Dla każdego punktu (x0,y0) wyznacza się jego odległość od prostej y=ax+b i wylicza (y0-ax0-b)2 a potem sumuje się uzyskane liczby. Wybiera się prostą dla której uzyskana suma jest najmniejsza. Metoda wyliczania takiej prostej nosi nazwę metody najmniejszych kwadratów, a prosta tak wyliczona nosi nazwę regresji (regresji z próby). Ma ona ogólną interpretację dla danych losowanych z rozkładu dwukrotnie normalnego. Założenia te dają następujące wzory na współczynniki prostej regresji:
Współczynniki prostej regresji łatwo jest zatem wyliczyć w R. Można dodać do wykresu rozrzutu wartości x można za pomocą funkcji abline(). Obowiązkowymi parametrami tej funkcji są dwie liczby, z których pierwsza to stała – punkt przecięcia wykreślanej prostej z osią 0Y, a druga to wsp. nachylenia czyli tangens kata nachylenia prostej do osi 0X. W skrypcie można zanotować następujący kod:
| x=1:10 y = c(5.76, 4.61, 7.59, 7.28, 7.34, 4.83, 10.71, 9.54, 12.23, 10.61) a=sum((x-mean(x))*(y-mean(y)))/sum((x-mean(x))^2) b=mean(y)-a*mean(x) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=FALSE) plot(x,y,col=”green2″, pch=15) abline(b,a,col=”green3″) # windows(4.5, 2.5) par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=TRUE) plot(x,y,col=”green2″, pch=15) abline(b,a,col=”green3″) |
Utworzony wykres na ogół spełnia wszystkie oczekiwania. Jeżeli jednak aktywna jest opcja xpd=TRUE funkcji par(), to linia trendu wyjdzie poza obszar kreślenia.
Tymczasem znacznie częściej linię trendu trzeba skrócić od minimalnej wartości x (w przykładzie 1) do maksymalnej wartości (w przykładzie 10). Wtedy lepiej skorzystać z funkcji podrzędnej lines(). Obowiązkowymi parametrami tej funkcji są współrzędne początku i końca linii zapisane jako c(min(x), max(x)) oraz c(min(y),max(y)). Można wykonać następujący program:
x=1:10
y = c(5.76, 4.61, 7.59, 7.28, 7.34, 4.83, 10.71, 9.54, 12.23, 10.61)
a=sum((x-mean(x))*(y-mean(y)))/sum((x-mean(x))^2)
b=mean(y)-a*mean(x)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(2,0.5,0), xpd=TRUE)
plot(x,y,col="green2", pch=15)
lines(c(min(x),max(x)),c(a*min(x)+b,a*max(x)+b), col="green3")
|
i uzyskać wykres:
W podanych programach parametry regresji wyliczane są ze wzorów. Tymczasem w R istnieje gotowa procedura na ich wyznaczenie. Służy do tego funkcja lm(), która zwraca tak naprawdę listę 12 różnych elementów, ale pierwszym elementem na liście są parametry (w kolejności b i a) prostej regresji y=ax+b. Tylko one się pokazują. Reszta wyników pojawia się gdy stosuje sie polecenia typu lm(y~x)[2] lub lm(y~x)[[5]]. Wygląda to następująco:
| > x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15) > y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12) > lm(y~x) # Call: lm(formula = y ~ x) # Coefficients: (Intercept) x -0.1084 1.3071 |
Przy tworzeniu wykresu rozrzutu danych z dodaną prostą regresji wystarczy zastosować funkcję abline() w postaci abline(lm(y~x)). Wykorzystano to w następującym programie:
x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15)
y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
plot(x,y)
abline(lm(y~x))
|
Wykonanie tego programu da w efekcie następujący wykres.
Trend
W biologii dość często pojawia się słowo trend (trend liniowy, trend rosnący, trend malejący, trend wykładniczy itp.). Słowa tego używano niegdyś jako szczególnej regresji, w której pierwsza zmienna (tzw. niezależna w myśl niezależności przyczynowo skutkowej) była wyrażana przez kolejne liczby (np. od 1 do 10 lub od 2001 do 2018). Odkąd jednak programy Microsoftu nazwały trendem każdą regresję (liniową i nieliniową) jest to synonim regresji. Do jego wyliczania używa się bowiem tak samo metody najmniejszych kwadratów.
Czasem jednak jest wygodniej użyć słowa trend, niż regresja, gdy na przykład wykazuje jak w czasie zmniejszał się w populacji procent samców żółwi w miarę ocieplenia klimatu. Procenty obrazujemy za pomocą słupków, a regresję wylicza się dla ich wartości. Wygląda to następująco:
x=c(1985, 1990, 1995, 2000, 2005, 2010, 2015)
y=c(51, 42, 38, 30, 21, 27, 18)
#
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
slup=barplot(y, names=x, ylab="Procent")
abline(lm(y~slup))
r=format(cor(slup,y),dig=3)
text(7.5,48,paste("r = ",r))
|
Wynikiem działania programu jest wykres słupkowy:
W programie nie użyto parametrów regresji między y a x, ale między y a środkami słupków, które są zapamiętywane w wektorze slup=barplot(). Funkcja barplot(), oprócz tego, że tworzy wykres, tworzy także wektor środków słupków, który można odczytać przez odpowiednie przypisanie. W tym typie wykresu układ współrzędnych dla słupków nie jest układem współrzędnych zależności y od x. Trzeba wyliczyć trend już po przeskalowaniu danych na rysunkowy układ współrzędnych.
Korelacja
Kwadrat korelacji, zwany współczynnikiem determinacji, odpowiednik odchylenia standardowego dla par punktów, definiuje się jako:
gdzie f(x) jest wartością regresji w punkcie x (czyli jest to ax+b). Ponieważ prosta, przyjmująca dla wszystkichch x stałą wartość równą średniej z wektora y, należy do rodziny funkcji, które dopasowujemy do danych metodą sumowania kwadratów odległości, licznik powyższego wzoru jest mniejszy niż mianownik. Im punkty są lepiej dopasowane do prostej regresji tym powyższy wzór daje większe liczby, a największą jest jeden.
Pierwiastek ze współczynnika determinacji R2, dodatni gdy nachylenie prostej regresji jest dodatnie i ujemny gdy nachylenie prostej regresji jest ujemne, nazywany jest współczynnikiem korelacji i oznaczany najczęściej jako r. Jego obliczanie w pracach biologicznych jest standardem. Po wprowadzeniu do niego wzorów na a i b dla regresji i kilku przekształceniach, można przekonać się, że:
Taki wzór znajdziecie we wszystkich podręcznikach statystyki.
Oczywiście w R istnieje prosta funkcja wyliczająca współczynnik korelacji dla dwóch dowolnych wektorów liczbowych. Jest nią funkcja cor(). Standardem jest umieszczanie wartości współczynnika korelacji na wykresach regresji. Wygląda to następująco:
x=c(1.84, 1.81, 1.04, 1.3, 0.27, 0.9, 1.97, 1.6, 1.92, 2.15)
y=c(3.28, 0.92, 1.95, 1.75, 0.39, 0.49, 2.04, 2.01, 1.31, 4.12)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
plot(x,y)
abline(lm(y~x))
r=format(cor(x,y),dig=3)
text(2,2.8,paste("r = ",r),srt=18)
|
Umiejscowienie napisu tak, by nie przesłaniało punktów oraz kąt obrotu, ustala się metoda prób i błędów.
Stężenie fluoru w wydzielinie gruczołów odbytowych skunksów i regresje liniowe dla wielu serii porównań
Baza danych, na której przykładzie pokazywane są różne programy w R, dotyczy samic i samców skunksów łowionych w trzech sezonach, które ważono i pobierano od nich próbki wydzieliny gruczołów odbytowych, a następnie określono stężenie fluoru w suchej masie tych próbek. Ta ramka danych została utworzona na podstawie danych pokazanych w części pierwszej “R Dla Biologów – Podstawowe Operacje” w rozdziale o ramkach danych w podroździale “Operacje na ramkach danych”.
Zobrazowanie zależności stężenia fluoru od ciężaru skunksów powinno być zrobione osobno grupach wyznaczonych przez ich płeć i sezon. Każda z 6 grup zwierząt powinna być zobrazowana przez inny kolor i powinna dla tej grupy zostać narysowana regresja w tym kolorze. Na początek można ustalić, że danym z wiosny dajemy kolor zielony (“green”), danym z jesieni kolor czerwony (“red”) a danym z zimy kolor niebieski (“blue”). Samice będą obrazowane przez pełne kółeczka (pch=19), a samce przez puste (pch=1). Tworzymy odpowiednie wektory pięćdziesięcioelementowe:
kolor=paste(1:50)
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="wiosna") kolor[i]="green"
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="jesień") kolor[i]="red"
for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="zima") kolor[i]="blue"
znak=1:50
for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samiec") znak[i]=1
for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samica") znak[i]=19
|
Pozwala to na narysowanie następującego wykresu:
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7,0.5,0))
plot(FLUOR~CIEZAR, skunks, col=kolor, pch=znak)
|
Powstaje w ten sposób wykres:
Następne instrukcje służyć będą do narysowania regresji dla każdej z grup punktów wyróżnionych przez PLEC i SEZON. Wykorzystana zostanie do tego funkcja
by(),
która podobnie jak
aggregate()
dzieli bazy danych na części wyróżnione przez wartości czynników, na których można potem wykonywać różne działania. W najprostszym przypadku instrukcja:
by(skunks, list(skunks$PLEC, skunks$SEZON),
function(x) x)
utworzy listę złożona z sześciu elementów, a każdy z tych elementów jest podbazą wyróżnioną przez wartości zmiennych dyskretnych. Parametry regresji, można wyliczyć za pomocą lm(y~x). Wykorzystując to można zastosować polecenie:
regresje =
by(skunks, list(skunks$PLEC, skunks$SEZON), function(x) lm(FLUOR~CIEZAR,x))
|
Pojawi się lista, której obejrzenie pokazuje, że wyniki ukazały się kolejno dla: samice-jesień, samiec-jesień, samice-wiosna, samiec-wiosna, samice-zima, samiec-zima. Ponieważ chcemy by kolory regresji zgadzały się z kolorem punktów i dla samic wyrażone były linią ciągłą, a dla samców przerywaną, to powinniśmy utworzyć następujące wektory kolorów i typów linii:
kolor.regresji = rep(c("red","green","blue"), each=2)
typ.regresji = rep(1:2,3)
|
Do wykonanego wykresu można teraz dodać linie trendu
for (i in 1:6) abline(regresje[[i]], col=kolor.regresji[i], lty=typ.regresji[i])
|
Powstaje w ten sposób następujący wykres;
Wykres ten ma wiele niedociągnięć. Po pierwsze nie ma legendy i w dodatku nie ma miejsca na legendę. Po drugie podpisy osi (domyślnie wstawiane nazwy kolumn bazy danych), są niepoprawne. Trzeba je wprowadzić. Aby utworzyć legendę i zmienić podpisy należy zebrać wszystkie instrukcje do skryptu i wykonać stosowne poprawki.
kolor=paste(1:50) for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="wiosna") kolor[i]="green" for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="jesień") kolor[i]="red" for (i in 1:50) if (as.vector(skunks$SEZON)[i]=="zima") kolor[i]="blue" znak=1:50 for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samiec") znak[i]=1 for (i in 1:50) if (as.vector(skunks$PLEC)[i]=="samica") znak[i]=19 windows(5.5, 2.5) # wydłużenie wykresu w poziomie o 1 cal) par(mar=c(3,3,1,10), mgp=c(1.7,0.5,0)) # wydłużenie prawego marginesu o 9 linijek) # dołączenie do funkcji plot() podpisów osi plot(FLUOR~CIEZAR, skunks, col=kolor, pch=znak, xlab="Ciężar [kg]", ylab=expression("Stężenie fluoru [ " * ng %.% g^-1 *"]" ) ) regresje = by(skunks, list(skunks$PLEC, skunks$SEZON), function(x) lm(FLUOR~CIEZAR,x)) kolor.regresji = rep(c("red","green","blue"), each=2) typ.regresji = rep(1:2,3) for (i in 1:6) abline(regresje[[i]], col=kolor.regresji[i], lty=typ.regresji[i]) # # dorysowanie legendy par(xpd=TRUE) legend(5,sum(par("usr")[3:4])/2, xjust=0, yjust=0.5, legend=c("samice wiosną", "samice-jesienią", "samice zimą", "samce wiosną", "samce jesienią", "samce zimą"), lty=c(1,1,1,2,2,2), pch=c(19,19,19,1,1,1), col=c("green", "red", "blue"), bty="n") |
Powstał w ten sposób wykres:
Wykres ten można dalej modyfikować. Można zmienić wielkość i krój czcionki, co opisano w rozdziale 8. Można użyć innych kolorów (rozdział 6), znaczników punktów (rozdział 7), zastosować kolorowe tło (rozdział 6). Można także zdecydować się na wyliczanie korelacji dla każdej regresji i dopisanie jej w odpowiednim miejscu i w odpowiednim kolorze na wykresie. Ma to znaczenie w przypadku gdy regresje są silnie nachylone, bo w przypadku pokazanych skunksów jest to zbędna informacja. Wystarczy tylko podpatrzeć, jak to zostało zaprogramowane, by wprowadzić stosowne poprawki do własnego kodu.
Koniec części III