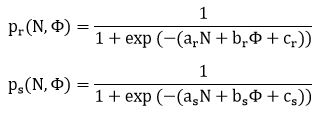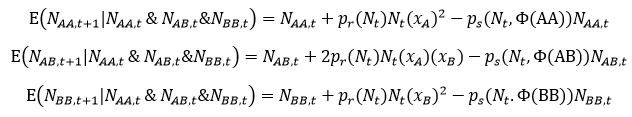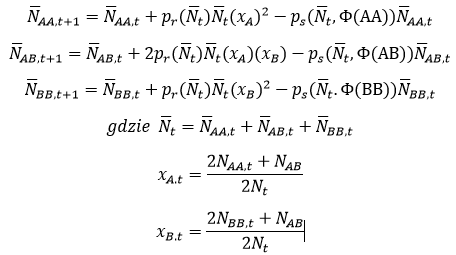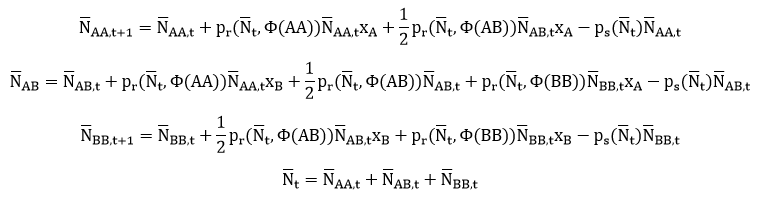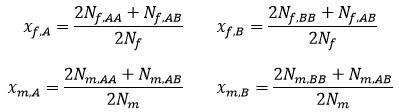Genotyp, Fenotyp i dobór naturalny
Genotyp i fenotyp
We wszystkich definicjach doboru naturalnego (ang. natural selection), które można znaleźć w encyklopediach i podręcznikach podkreślane są następujące elementy:
- Osobniki w populacjach nie są jednakowe. Różnią się fenotypem, a fenotyp wpływa na ich dostosowanie (adaptację) do lokalnych warunków środowiska (co ostatecznie zmienia ich prawdopodobieństwo śmierci, prawdopodobieństwo rozrodu lub liczbę jednorazowo rodzonych potomków).
- Choć na fenotyp osobnika wpływają warunki środowiskowe w okresie jego wzrostu i rozwoju, w największym stopniu zależy on od genotypu osobnika (stąd podobieństwo potomstwa do osobników rodzicielskich).
- Osobniki o genotypie związanym z lepszym dostosowaniem (czyli o mniejszym prawdopodobieństwem śmierci lub większym prawdopodobieństwem rozrodu lub wydające na świat jednorazowo więcej potomstwa) wypierają z populacji osobniki pozostałe co ostatecznie prowadzi do zmian w strukturze genetycznej populacji i jej ewolucji.
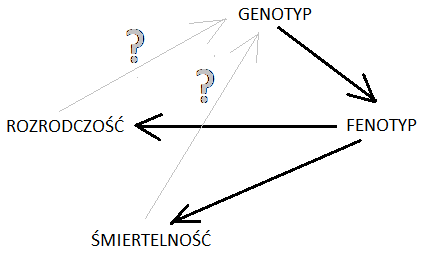
O ile istnienie zróżnicowania fenotypów wpływających na zróżnicowanie rozrodczości i przeżywalności osobników oraz istnienie genotypów wpływających na fenotyp można uznać za fakty, to zjawisko kierunkowe zmiany struktury genetycznej populacji w kierunku mniejszej śmiertelności lub większej rozrodczości powinno pojawić się spontanicznie. Nie powinno być modelowane. Zmodyfikowany obiektowy model populacji o rozrodzie Mendlowskim będzie modyfikowany tylko poprzez wprowadzenie fenotypu do klasy jaką jest osobnik, związku między genotypem a fenotypem i uzależnieniem prawdopodobieństw śmierci i/lub rozrodu od fenotypu.
Na rysunku czarnymi strzałkami oznaczono to, co powinno być zaprogramowane jako zależność funkcyjna, a cienkimi szarymi strzałkami to, do czego wystarczy dopisać instrukcje zbierające informacje o stanie populacji w kolejnych pokoleniach.
Programowanie fenotypu na podstawie genotypu i zależności śmiertelności i rozrodczości od fenotypu
Ponieważ nie tworzymy modelu z mutacjami genów, to te geny, które istnieją w populacji początkowej, będą w niej istniały, dopóki któryś nie zniknie. Mając geny o dwóch allelach A i B wystarczy przy programowaniu zależności fenotypu od genotypu ograniczyć się do zwykłego przyporządkowania. A → Fenotyp 1, B → Fenotyp 2.
Gdy fenotyp jest liczbą, to może wpływać na prawdopodobieństwa śmierci lub rozrodu za pomocą funkcji dwuargumentowych:
Wybranie dodatniego parametru br spowoduje wzrost prawdopodobieństwa rozrodu, a wybranie dodatniego parametru bs wzrost prawdopodobieństwa śmierci. Wiele fenotypów wpływa tylko na jedno s tych prawdopodobieństw. Wtedy druga wartość br lub bs będzie równa 0.
Zależność między genotypem a fenotypem oznacza właściwie wszystko, czym zajmują się biolodzy w różnych instytutach i zakładach. W modelu zrobimy to najprościej, jak się da. Na przykład, poprzez przyporządkowanie genotypom z góry założonych wartości: liczby Φ.
| Genotyp | Fenotyp |
|---|---|
| AA | 0 |
| AB | 1 |
| BB | 2 |
Będziemy manipulować wartościami fenotypu i różnie je przyporządkowywać genotypom. Rozważymy tylko wpływ fenotypu na prawdopodobieństwo śmierci osobnika powodując jej zmniejszenie się w miarę wzrostu fenotypu (parametr bs ujemny a br równy 0). Notować będziemy liczby osobników o genotypach AA, AB i BB z pokolenia na pokolenie i będziemy sprawdzać frakcje allelu A w puli genowej populacji.
Symulator populacji po zaproponowanych zmianach wygląda następująco:
from random import random, randrange
from math import exp
def fen(x,y):
if (x=="A" and y=="A"):
return 0
elif (x=="B" and y=="B"):
return 0
else:
return 0
class stanosobnika:
NR=0
GEN1=''
GEN2=''
FEN=0
populacja=[]
populacja1=[]
N0=100
ar=-0.005
br=1
ass=0.005
bs=-0.1
cs=0
czas=500
lpow=20
tekst='Powtorzenie, Czas, N, NAA, NAB, NBB, NA, NB \n'
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
nA=0
nB=0
nAA=0
nBB=0
nAB=0
for i in range(N0):
osob=stanosobnika()
osob.NR=i
if i<N0/2:
osob.GEN1='A'
nA=nA+1
else:
osob.GEN1='B'
nB=nB+1
if (i=3*N0/4):
osob.GEN2='A'
nA=nA+1
else:
osob.GEN2='B'
nB=nB+1
if (osob.GEN1=='A' and osob.GEN2=="A"):
nAA=nAA+1
elif (osob.GEN1=="B" and osob.GEN2=="B"):
nBB=nBB+1
else:
nAB=nAB+1
osob.FEN=fen(osob.GEN1,osob.GEN2)
populacja.append(osob)
N=N0
ostnr=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + ", " + str(nAA) + ", "
tekst=tekst + str(nAB) + ", " + str(nBB) + ", " + str(nA) + ", " + str(nB) +"\n"
for t in range(1,czas+1):
n=0
for i in range(N):
osob=populacja[i]
pr=1/(1+exp(-(ar*N+br)))
ps=1/(1+exp(-(ass*N+bs*osob.FEN+cs)))
if random()<pr:
potom=stanosobnika()
potom.NR=ostnr+1
ostnr=ostnr+1
if random()<0.5:
potom.GEN1=osob.GEN1
else:
potom.GEN1=osob.GEN2
ojciec=populacja[randrange(N)]
if random()<0.5:
potom.GEN2=ojciec.GEN1
else:
potom.GEN2=ojciec.GEN2
potom.FEN=fen(potom.GEN1,potom.GEN2)
populacja1.append(potom)
n=n+1
if random()100000:
break
nAA=0
nBB=0
nAB=0
nA=0
nB=0
for i in range(N):
osob=populacja1[i]
if osob.GEN1=='A':
nA=nA+1
else:
nB=nB+1
if osob.GEN2=='A':
nA=nA+1
else:
nB=nB+1
if (osob.GEN1=='A' and osob.GEN2=="A"):
nAA=nAA+1
elif (osob.GEN1=="B" and osob.GEN2=="B"):
nBB=nBB+1
else:
nAB=nAB+1
populacja=populacja1
populacja1=[]
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + ", " + str(nAA) + ", "
tekst=tekst + str(nAB) + ", " + str(nBB) + ", " + str(nA) + ", " + str(nB) +"\n"
populacja=[]
tekst=tekst+"\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Program ten jest nieznacznie zmodyfikowanym programem omówionym przez studentów zajmującym się dryfem genetycznym i prawem Hardy’ego Weinberga.
Uzależnienie prawdopodobieństwa śmierci od fenotypu i obliczanie przewidywane liczebności osobników o określonym genotypie
Dla rozważanego modelu obowiązują następujące wzory dla ciągów rekurencyjnych wyliczających warunkowe wartości oczekiwane liczby osobników o danym genotypie NAA,t, NAB,t i NBB,t w kolejnych krokach czasowych:
gdzie Nt=NAA,t+NAB,t+NBB,t, xA jest frakcją genów o allelu A w puli genowej populacji, a xB jest frakcją genów o allelu B w puli genowej populacji.
Wynikają z tego następujące wzory na przewidywane dynamiki liczebności populacji:
Gdy uruchomi się go z jednakowymi wartościami funkcji fen() dla wszystkich genotypów uzyskamy model dryfu genetycznego. Ze zróżnicowanymi wartościami tej funkcji, ale takimi, że fenotyp(AA)≤fenotyp(AB)≤fenotyp(BB) albo fenotyp(AA)≥fenotyp(AB)≥fenotyp(BB) utworzy się model z kierunkowym doborem naturalnym. Co się stanie gdy fenotyp(AA)<fenotyp(AB)>fenotyp(BB)?
Zadanie pierwsze dla studentów
Otworzyć pusty plik arkusza kalkulacyjnego Excel lub Calc. W polach A1, A2, A3, A4, A5 wpisać nazwy parametrów modelu (ar, br, as, bs, cs), a w polach B1, B2, B3, B4, B5 przepisanymi z programu wartościami tych parametrów.
W polu A6 wpisać fen(AA),W polu A7 wpisać fen(AB),W polu A8 wpisać fen(BB), a w pola B6, B7 i B8 wartości tych funkcji zastosowanych w programie.
W polu c1 wpisać “Liczebność”, a w pola C2:C502 liczby od 0 do 500.
W polu D1 wpisać “psAA”, w polu D2 formułę =1/(1+exp(-($b$3*C2+$B$4*$B$6+$B$5))) i przeciągnąć ją do pola D502.
W polu E1 wpisać “psAB”, w polu E2 formułę =1/(1+exp(-($b$3*C2+$B$4*$B$7+$B$5))) i przeciągnąć ją do pola E502.
W polu F1 wpisać “psBB”, w polu F2 formułę =1/(1+exp(-($b$3*C2+$B$4*$B$8+$B$5))) i przeciągnąć ją do pola F502.
Zaznaczyć kolumny od C do F i zrobić wykres zależności prawdopodobieństw śmierci osobnika o określonym genotypie od liczebności populacji (punktowy, podtyp liniowy).
Zatytułować wykres, podpisać osie i zrobić legendę (w niej wystarczy wypisać genotypy osobników: AA, AB i BB)
Spróbujemy teraz przewidzieć jak będzie zmieniała się liczba osobników o danym genotypie.
W polu H1 wpisać “czas” a w polach H2:H502 liczby od 0 do 500.
W polu I1 wpisać “pr”. W polach J1, K1, L1 wpisać psAA, psAB i psBB odpowiednio.
W polach M1, N1 i O1 wpisać NAA, NAB i NBB odpowiednio. Będą w nich wyliczane liczby osobników o danych genotypach.
W pola P1 i Q1 wpisać “xA” i “xB”. Tu będą wyliczane frakcje genów A i genów B w puli genowej populacji.
W polach M2 liczebność początkową osobników o genotypie AA: np. 25.
W polu N2 wpisać formułę =2*((M2/100)^(1/2))*(1-((M2/100)^(1/2)))*100
W polu O2 wpisać formułę =((1-((M2/100)^(1/2)))^2)*100
W ten sposób liczebności początkowe poszczególnych genotypów będą na początku w równowadze Hardy’ego-Weinberga a suma tych osobników będzie równa 100, nie zależnie jaką liczbę wpisze się do pola M2.
W polu P2 wyliczyć frakcję genów A w puli genowej. W polu Q2 wyliczyć frakcje genów B w puli genowej. Przypominam, że frakcje te wyliczane są wg wzoru:
Należy samemu napisać odpowiednią formułę po znaku = odwołując się do komórek M2, N2 i O2.
W polu I3 należy wpisać formułę =1/(1+exp(-($B$1*(M2+N2+O2)+$B$2)))
W polu J3 należy wpisać formułę =1/(1+exp(-($B$3*(M2+N2+O2)+$B$4*$B$6+$b$5)))
W polu K3 należy wpisać formułę =1/(1+exp(-($B$3*(M2+N2+O2)+$B$4*$B$7+$b$5)))
W polu L3 należy wpisać formułę =1/(1+exp(-($B$3*(M2+N2+O2)+$B$4*$B$8+$b$5)))
W polu M3 należy wpisać formułę =M2+I3*(M2+N2+O2)*P2^2-J3*M2
W polu N3 należy wpisać formułę =N2+I3*(M2+N2+O2)*2*P2*Q2-K3*N2
W polu O3 należy wpisać formułę =O2+I3*(M2+N2+O2)*Q2^2-L3*O2
Formuły z pół P2 i Q2 przeciągnąć do P3 i Q3. Zaznaczyć pola od H3 do Q3 i przeciągnąć wszystkie formuły do wiersza 502.
Wykonać wykres zmian w czasie frakcji allelu A (czas i kolumna P). frakcja allelu B to 1-frakcja allelu A i nie trzeba jej rysować. Zatytułować, podpisać osie, legendę.
Sprawdzić, jak będą zmieniały się frakcje allelu A, gdy populacje początkowe będą różniły się składem genotypowym. W tym celu w pole M2 wprowadzać różne liczby z zakresu od 0 do 100 (np. 5, 10, 15, …, 95) i obserwować zmiany przewidywanych frakcji genów o allelu A. Aby zobrazować to na jednym wykresie należy pole z frakcjami kopiować (najlepiej do innego arkusza, gdzie wcześniej zostanie skopiowana kolumna H) metodą wklej wartości. Następnie wykonać wykres zależności przewidywanych frakcji genów o allelu A od czasu, dla różnego składu genotypowego populacji początkowej.
Wykonać symulację podanego programu bez zmiany liczebności początkowych.
Wyniki przenieść do Excela, tak by znalazły się w 8 kolumnach. Skopiować je do wcześniej wykonanego pliku excelowego.
W pliku Excelowym w polu M2 wpisać 25 (taką liczebność mają w programie liczby osobników populacji początkowej o genotypie AA).
Wyliczyć w osobnej kolumnie frakcje allelu A uzyskane podczas symulacji. Zobrazować zależność frakcji allelu A od czasu na jednym wykresie dla 20 powtórzeń (wykres punktowy z liniami). Dołączyć te wyniki do wcześniej wykonanego wykresu przewidywanej frakcji allelu A.
Doprowadzić wykresy do stanu, w którym będą prezentowane (powiększyć czcionkę, zlikwidować niepotrzebne elementy, dobrać kolory, tło itd.). Nazwać plik zapamiętać.
Wykonany wykres obrazuje sytuacje “zerową” i będzie służył do porównań z wykresami zrobionymi dla populacji, dla których założono następujące wartości funkcji fenotyp():
|
|
|
Skopiować wcześniej wykonany plik Excela/Calca. Otworzyć kopię. Podmienić odpowiednie wartości w polach B6, B7 i B8. Powinno to zmienić automatycznie wszystko co dotyczy krzywych przewidywanych.
Zmieniać liczebności początkowe w polu M2 liczbami z zakresu od 0 do 100. Kopiować kolumnę ze zmianami frakcji genów o allelu A metodą wklej wartości w miejsce istniejących danych z modelu zerowego. Wykres powinien się odpowiednio zmodyfikować sam.
Zmodyfikować odpowiednio program (tzn. funkcję fenotyp) i wykonać symulację.
Wyniki przenieść do Excela tak by były w 8 kolumnach. Skopiować całą zawartość do kopii pierwszego pliku w miejsce poprzednich wyników symulacji. Powinno to automatycznie podmienić wykres trzeci.
Ponownie wykonać kopie pliku, zmienić wartości funkcji fenotyp w arkuszu kalkulacyjnym i programie symulacyjnym. Wykonać symulację i podmienić wyniki symulacji.
Wszystkie czynności powtórzyć dla kolejnego zestawu wartości funkcji fenotyp.
Zatytułować wykresy, podpisać osie, zapamiętać.
Uzależnienie prawdopodobieństwa rozrodu od fenotypu
Uzależnienie prawdopodobieństwa rozrodu od fenotypu w programie symulacyjnym wymaga modyfikacji poprzedniego programu.
from random import random, randrange
from math import exp
def fenotyp(x,y):
if (x=="A" and y=="A"):
return 0
elif (x=="B" and y=="B"):
return 2
else:
return 1
class stanosobnika:
NR=0
GEN1=''
GEN2=''
FEN=0
populacja=[]
populacja1=[]
N0=100
ar=-0.005
br=0.1
cr=1
ass=0.005
bs=0
czas=500
lpow=20
tekst='Powtorzenie, Czas, N, NAA, NAB, NBB, NA, NB \n'
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
nA=0
nB=0
nAA=0
nBB=0
nAB=0
for i in range(N0):
osob=stanosobnika()
osob.NR=i
if i<N0/2:
osob.GEN1='A'
nA=nA+1
else:
osob.GEN1='B'
nB=nB+1
if (i<N0/4 or i>=3*N0/4):
osob.GEN2='A'
nA=nA+1
else:
osob.GEN2='B'
nB=nB+1
if (osob.GEN1=='A' and osob.GEN2=="A"):
nAA=nAA+1
elif (osob.GEN1=="B" and osob.GEN2=="B"):
nBB=nBB+1
else:
nAB=nAB+1
osob.FEN=fenotyp(osob.GEN1,osob.GEN2)
populacja.append(osob)
N=N0
ostnr=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + ", " + str(nAA) + ", "
tekst=tekst + str(nAB) + ", " + str(nBB) + ", " + str(nA) + ", " + str(nB) +"\n"
for t in range(1,czas+1):
n=0
for i in range(N):
osob=populacja[i]
pr=1/(1+exp(-(ar*N+br*osob.FEN+cr)))
ps=1/(1+exp(-(ass*N+bs)))
if random()<pr:
potom=stanosobnika()
potom.NR=ostnr+1
ostnr=ostnr+1
if random()<0.5:
potom.GEN1=osob.GEN1
else:
potom.GEN1=osob.GEN2
ojciec=populacja[randrange(N)]
if random()<0.5:
potom.GEN2=ojciec.GEN1
else:
potom.GEN2=ojciec.GEN2
potom.FEN=fenotyp(potom.GEN1,potom.GEN2)
populacja1.append(potom)
n=n+1
if random()<ps:
pass
else:
populacja1.append(osob)
n=n+1
N=n
if N>100000:
break
nAA=0
nBB=0
nAB=0
nA=0
nB=0
for i in range(N):
osob=populacja1[i]
if osob.GEN1=='A':
nA=nA+1
else:
nB=nB+1
if osob.GEN2=='A':
nA=nA+1
else:
nB=nB+1
if (osob.GEN1=='A' and osob.GEN2=="A"):
nAA=nAA+1
elif (osob.GEN1=="B" and osob.GEN2=="B"):
nBB=nBB+1
else:
nAB=nAB+1
populacja=populacja1
populacja1=[]
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + ", " + str(nAA) + ", "
tekst=tekst + str(nAB) + ", " + str(nBB) + ", " + str(nA) + ", " + str(nB) +"\n"
populacja=[]
tekst=tekst+"\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Inaczej trzeba wykonać matematyczną analizę analizowanych zmiennych.
Prawdopodobieństwa wylosowania genu ojcowskiego dla potomka o określonym allelu będzie równe frakcji tych genów w puli genowej populacji. Dokładnie będą one równe:
gdzie NAA jest liczbą osobników w chwili t o genotypie AA, NAB jest liczba osobników o genotypie AB i NBB jest liczba osobników o genotypie BB, a N liczebnością całej populacji. Potomek uzyskuje genotyp AA gdy jego osobnik macierzysty był AA a gen ojcowski został wylosowany z prawdopodobieństwem xA oraz gdy osobnik macierzysty miał genotyp AB, został z prawdopodobieństwem 0.5 wylosowany gen A a gen ojcowski został wylosowany z prawdopodobieństwem xA. Oznacza to, że wartość oczekiwana potomków o genotypie AA jest równa:
Potomek będzie miał genotyp AB gdy osobnik macierzysty będzie miał genotyp AA i wylosowany zostanie gen ojcowski o allelu B oraz gdy osobnik macierzysty będzie miał genotyp AB z którego zostanie z prawdopodobieństwem 0.5 wylosowany gen A i a wylosowany gen ojcowski będzie miał allel B oraz gdy osobnik macierzysty będzie miał genotyp AB z którego zostanie z prawdopodobieństwem 0.5 wylosowany gen B i a wylosowany gen ojcowski będzie miał allel A oraz gdy osobnik macierzysty będzie miał genotyp BB i zostanie wylosowany gen ojcowski o allelu A. Oznacza to, że wartość oczekiwana liczby potomków o genotypie AB jest równa:
Potomek będzie miał genotyp BB gdy osobnik macierzysty będzie miał genotyp AB i z prawdopodobieństwem 0.5 zostanie wylosowany gen o allelu B i gen ojcowski będzie miał allel B oraz gdy osobnik macierzysty będzie miał genotyp BB i gen ojcowski będzie miał allel B. Wartość oczekiwana liczby potomków o genotypie BB będzie równa:
We wzorach tych p(N,AA), p(N,AB) i p(N,BB) są skrótowym zapisem prawdopodobieństw wyliczanych ze wzoru p(N,fenotyp(‘A’,’A’)), p(N,fenotyp(‘A’,’B’)) i p(N,fenotyp(‘B’,’B’)).
Oznacza to, że wartości przewidywane liczb osobników o danym genotypie w chwili t tworzą następujący układ ciągów rekurencyjnych:
Zadanie drugie dla studentów
Otworzyć pusty plik Excela lub Calca, albo skopiować któryś z plików wykonanych w kroku pierwszym, co pozwoli na zachowanie formatowania wykresów i trochę wprowadzonych już elementów. W dalszym ciągu opis dotyczyć będzie sytuacji, gdy drugą część zadania robi ktoś od początku.
W polach A1, A2, A3, A4, A5 wpisać nazwy parametrów modelu (ar, br, cr, as, bs), a w polach B1, B2, B3, B4, B5 przepisać z programu wartości tych parametrów.
W polu A6 wpisać fen(AA),W polu A7 wpisać fen(AB),W polu A8 wpisać fen(BB), a w pola B6, B7 i B8 wartości tych funkcji zastosowanych w programie.
W polu c1 wpisać “Liczebność”, a w pola C2:C502 liczby od 0 do 500.
W polu D1 wpisać “prAA”, w polu D2 formułę =1/(1+exp(-($b$1*C2+$B$2*$B$6+$B$3))) i przeciągnąć ją do pola D502.
W polu E1 wpisać “prAB”, w polu E2 formułę =1/(1+exp(-($b$1*C2+$B$2*$B$7+$B$3))) i przeciągnąć ją do pola E502.
W polu F1 wpisać “prBB”, w polu F2 formułę =1/(1+exp(-($b$1*C2+$B$2*$B$8+$B$3))) i przeciągnąć ją do pola F502.
Zaznaczyć kolumny od C do F i zrobić wykres zależności prawdopodobieństw śmierci osobnika o określonym genotypie od liczebności populacji (punktowy, podtyp liniowy).
Zatytułować wykres, podpisać osie i zrobić legendę (w niej wystarczy wypisać genotypy osobników: AA, AB i BB)
Spróbujemy teraz przewidzieć jak będzie zmieniała się liczba osobników o danym genotypie.
W polu H1 wpisać “czas” a w polach H2:H502 liczby od 0 do 500.
Spróbujemy teraz przewidzieć jak będzie zmieniała się w czasie liczba osobników o danym genotypie.
W polu H1 wpisać “czas” a w polach H2:H502 liczby od 0 do 500.
W polu I1, J1, K1 wpisać prAA, prAB i prBB odpowiednio. W polach L1 wpisać ps odpowiednio.
W polach M1, N1 i O1 wpisać NAA, NAB i NBB odpowiednio. Będą w nich wyliczane liczby osobników o danych genotypach.
W pola P1 i Q1 wpisać “xA” i “xB”. Tu będą wyliczane frakcje genów A i genów B w puli genowej populacji.
W polach M2 liczebność początkową osobników o genotypie AA: np. 25.
W polu N2 wpisać formułę =2*((M2/100)^(1/2))*(1-((M2/100)^(1/2)))*100
W polu O2 wpisać formułę =((1-((M2/100)^(1/2)))^2)*100
W ten sposób liczebności początkowe poszczególnych genotypów będą na początku w równowadze Hardy’ego-Weinberga a suma tych osobników będzie równa 100, nie zależnie jaką liczbę wpisze się do pola M2.
W polu P2 wyliczyć frakcję genów A w puli genowej. W polu Q2 wyliczyć frakcje genów B w puli genowej. Przypominam, że frakcje te wyliczane są wg wzoru:
Należy samemu napisać odpowiednią formułę po znaku = odwołując się do komórek M2, N2 i O2.
W polu I3 należy wpisać formułę =1/(1+EXP(-($B$1*(M2+N2+O2)+$B$2*$B$6+$B$3)))
W polu J3 należy wpisać formułę =1/(1+EXP(-($B$1*(M2+N2+O2)+$B$2*$B$7+$B$3)))
W polu K3 należy wpisać formułę =1/(1+exp(-($B$1*(M2+N2+O2)+$B$2*$B$8+$b$3)))
W polu L3 należy wpisać formułę =1/(1+EXP(-($B$4*(M2+N2+O2)+$B$5)))
W polu M3 należy wpisać formułę =M2+I3*M2*P2+0.5*J3*N2*P2-L3*M2
W polu N3 należy wpisać formułę =N2+I3*M2*Q2+0.5*J3*N2+K3*O2*P2-L3*N2
W polu O3 należy wpisać formułę =O2+0.5*J3*N2*Q2+K3*O2*Q2-L3*O2
Zaznaczyć pola od I3 do O3 i przeciągnąć formuły do wiersza 502.
Wykonać wykres zmian w czasie frakcji allelu A (czas i kolumna P). frakcja allelu B to 1-frakcja allelu A i nie trzeba jej rysować. Zatytułować, podpisać osie, legendę.
Sprawdzić jak będą zmieniały się frakcje allelu A, gdy populacje początkowe będą różniły się składem genotypowym. W tym celu w pole M2 wprowadzać różne liczby z zakresu od 0 do 100 (np. 5, 10, 15, …,95) i obserwować zmiany przewidywanych frakcji genów o allelu A. Aby zobrazować to na jednym wykresie, należy pole z frakcjami kopiować (najlepiej do innego arkusza, gdzie wcześniej zostanie skopiowana kolumna H) metodą wklej wartości. Następnie wykonać wykres zależności przewidywanych frakcji genów o allelu A od czasu, dla różnego składu genotypowego populacji początkowej.
Wykonać symulację podanego programu bez zmiany liczebności początkowych.
Wyniki przenieść do Excela, tak by znalazły się w 8 kolumnach. Skopiować je do wcześniej wykonanego pliku excelowego.
W pliku Excelowym w polu M2 wpisać 25 (taką liczebność mają w programie liczebności osobników populacji początkowej o genotypie AA).
Wyliczyć w osobnej kolumnie frakcje allelu A uzyskane podczas symulacji. Zobrazować zależność frakcji allelu A od czasu na jednym wykresie dla 20 powtórzeń (wykres punktowy z liniami). Dołączyć te wyniki do wcześniej wykonanego wykresu przewidywanej frakcji allelu A.
Doprowadzić wykresy do stanu, w którym będą pokazywane na prezentacji (powiększyć czcionkę, zlikwidować niepotrzebne elementy, dobrać kolory, tło itd.). Nazwać plik, zapamiętać.
Skopiować wykonany plik i powtórzyć wykonane czynności dla zmienionych wartości funkcji fen():
|
|
W tym celi podmieniać wartości funkcji fen() na kopii. Część rzeczy zmieni się automatycznie i tylko wykres zależności przewidywanych frakcji genów o allelu A od czasu, wymagać będzie nieco pracy. W przypadku danych symulowanych wystarczy zmodyfikować wartości funkcji fen() w programie, wykonać symulację, wprowadzić do Excela i podmienić wartości w kopii. Wykres powinien sie automatycznie zaktualizować.
Zatytułować wykresy, podpisać osie, zapamiętać.
- Zwrócić uwagę, że z informatycznego punktu widzenia, modyfikowanie osobnika poprzez wprowadzanie mu zmiennej FEN nie było konieczne. Wystarczyło uzależnić funkcje pr(N,Φ) i ps(N,Φ) bezpośrednio od funkcji fen(). Zrobiono to jednak, aby upodobnić dobór naturalny do rzeczywistego zjawiska. Ponadto ma to znaczenie gdy komplikuje się dalej model wprowadzając mutacje genów i tworząc klasyczne modele ewolucji, w którym mutacje zawsze tworzą nowy allel (modele ewolucji molekularnej) oraz powodują losowe zmiany fenotypu (modele ewolucji morfologicznej). Okazuje się, że wystarczy odpowiednio zmodyfikować geny osobników wirtualnych by można było je zmieniać poprzez losowe mutacje. Funkcja fen() staje się wtedy niepotrzebna, natomiast obecność zmiennej FEN w klasie jaka jest osobnik – niezbędna. Oba rodzaje ewolucji pojawiają się wtedy spontanicznie podczas symulacji.
- Zwrócić uwagę, jak niewielkie różnice między prawdopodobieństwami dla różnych fenotypów wystarczają by ukierunkować dryf genetyczny. Poprzez porównanie wykresów prawdopodobieństw śmierci/rozrodu osobników o różnych genotypach w zależności od liczebności populacji.
- Ocenić stabilność procesu na podstawie wykonanych wykresów zależności przewidywanych dynamik frakcji allelu A przy różnej strukturze genotypowej populacji początkowych (odpowiednie definicje są podane w temacie “stabilność, niestabilność i chaos”).
- Zwrócić uwagę na fakt, że uzależnienie prawdopodobieństwa rozrodu od fenotypu nie jest ani równoważne ani odwróceniem uzależnienia prawdopodobieństw śmierci od fenotypu. W czym tkwią różnice?
Istnieje jeszcze jeden rodzaj doboru naturalnego, który nie został omówiony w tym rozdziale. Jest to uzależnienie prawdopodobieństwa zostania ojcem od fenotypu osobników (jakości plemników lub pyłku). Niektórzy traktują to, jako dobór płciowy, ale nie jest to zgodne z jego klasyczną definicją wprowadzoną do nauki przez Karola Darwina. Jego definicja dotyczyła populacji rozdzielnopłciowych i związana była z tym, że osobniki jednej płci aktywnie wybierają sobie partnerów drugiej płci kierując się ich fenotypem. Wszelkie zmiany fizjologiczne osobników zwiększające ich sukces rozrodczy zaliczył do doboru naturalnego. Pozostałe rodzaje doboru naturalnego nie dotyczą już modeli najprostszych populacji, w której nie wyróżnia się bezpłodnych okresów dojrzewania, możliwość urodzenia jednocześnie wielu potomków itd.