Model najprostszej populacji
Osobnik jako obiekt
Choć definicji terminu “populacja” jest bardzo dużo, zgadzają się one w jednym – określają populację jako zbiór osobników (w różny sposób zależnych od siebie, komunikujących się ze sobą, rywalizujących o te same zasoby, cechujących się swobodnym przepływem genów itd.). Tworząc populacje wirtualne przede wszystkim należy zdefiniować osobnika.
Osobnik jest to jednostkowy przedstawiciel populacji, który rodzi się, żyje i umiera. Podczas życia rozmnaża się tworząc osobniki potomne. Zdarzenia takie jak rozród i śmierć dotyczą go osobiście i tylko prawdopodobieństwa tych zdarzeń mogą zależeć bezpośrednio i pośrednio od pozostałych osobników populacji. Informatyk powiedziałby, że osobniki są kompartmentami i wyznaczyłby zbiór cech (zmiennych) wspólnych dla wszystkich osobników danej populacji, w której osobniki różnią się między sobą co najwyżej wartościami tych cech. Innymi słowy zdefiniował by prosty obiekt typu ‘class’, w którym poszczególne cechy maja jakieś wartości domyślne, ale tworząc populacje takich osobników, każdy z nich ma swoje indywidualne wartości, często zmieniające się w czasie. Osobnik taki (a właściwie jego stan w chwili np. narodzin) mógłby wyglądać następująco:
class stanosobnika:
NR=0
WIEK=0
PLEC='F'
WZROST=53
CIEZAR=3.2
class GENOTYP:
GEN1='A'
GEN2='B'
|
Przypomina to bardzo opis osobników po wykonaniu badań terenowych, gdzie osobniki się mierzy, waży, ocenia ich płeć i określa inne ich cechy. Często próbki tkanek tych osobników poddaje się jeszcze badaniom chemicznym i genetycznych dodając dodatkowe zmienne charakteryzujące danego osobnika. Dotyczy to także pozornie niepotrzebnej zmiennej NR (indywidualny numer osobnika), gdyż w badaniach poszczególne osobniki analizowanej próby zawsze się numeruje. W modelach numerowanie osobników jest potrzebne głównie do uzyskiwania wielu wartości zwrotnych dotyczących charakterystyk całego wirtualnego życia osobnika (długości życia osobnika, liczby jego rozrodów, liczby posiadanych przez niego potomków itp.). Modele tworzone z używaniem indywidualnego nazywania osobników są modelami osobniczymi, w których populacje można charakteryzować poprzez historie życia poszczególnych jej przedstawicieli.
Stan osobnika jako klasa, jest jedną z najprostszych klas rozpatrywanych w Pythonie i raczej nie warto ich bardziej komplikować. Gdy dodajemy do niego wszystkie zmienne związane ze zdobywaniem doświadczenia życiowego, uczeniem się itp. warto je skupiać w osobną klasę (class mózg), gdyż przy obfitości zmiennych, jakimi posługujemy się opisując osobniki, ułatwia to programowanie. Przy programowaniu graficznym obowiązują te same reguły, jak w grach komputerowych przy określaniu kształtu, wielkości, koloru i umiejscowienia osobnika na ekranie. Wtedy obiekt ‘class stanosobnika’ uzupełniany jest o parametry, które umożliwiają jego pokazanie i często poruszanie się osobników, na ekranie komputera.
Najprostsza populacja
Najprostsza populacja składa się z najprostszych osobników. Ich stan ogranicza się do ich indywidualnego numeru i ewentualnie tych zmiennych, które umożliwiają pokazanie osobników na ekranie. Uwzględnione natomiast zostają zjawiska występujące we wszystkich populacjach:
- Osobniki rodzą się (wykluwają się, kiełkują lub powstają po podziale komórki).
- osobniki rozradzają się (przynajmniej niektóre).
- Osobniki umierają.
W najprostszej populacji zjawiska rozrodu i śmierci programujemy jako zjawiska losowe. Eksperymentalny model najprostszej populacji wyglądałby następująco.
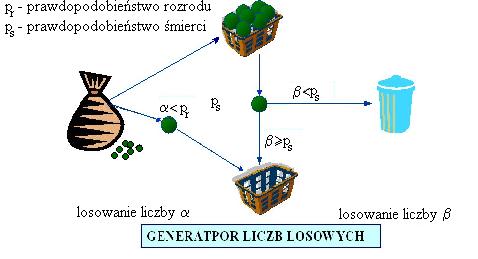
Generator liczb losowych to na przykład 10 001 karteczek z liczbami od 0 do 1 z czterema liczbami po separatorze dziesiętnym.
Eksperyment wygląda następująco:
- Tworzymy stan populacji w chwili 0 wrzucając do jakiegoś pojemnika odpowiednią liczbą osobników z ustalonymi charakterystykami początkowymi.
- Następnie wybieramy z populacji osobnika i losujemy z generatora dwie karteczki.
- Sprawdzamy czy liczba na pierwszej karteczce jest mniejsza od prawdopodobieństwa rozrodu. Jeżeli tak, do populacji w kroku następnym dodajemy osobnika w wieku 0. Jeżeli nie jest, to nic nie robimy.
- Sprawdzamy czy liczba na drugiej karteczce jest mniejsza od prawdopodobieństwa śmierci. Jeżeli tak, to osobnika wyrzucamy do kosza, jeżeli nie to wiek osobnika zwiększa się o 1, wielkość zwiększa się o przyrost wyliczony z jakiejś krzywej wzrostu itd. Aktualizujemy tak wszystkie charakterystyki osobnika i umieszczamy go w pojemniku będącym umownie stanem populacji w chwili następnej.
- Postępujemy tak dla wszystkich osobników z populacji, aż wszystkie znajdą się w tym pojemniku. Po tych czynnościach czas zwiększa się o 1, stan populacji w chwili następnej staje się stanem aktualnym i można zacząć wszystko od nowa.
Model najprostszej populacji, to po prostu zaprogramowany opisany eksperyment. Wymaga on, jak widać, określenia liczbowo wielkości populacji początkowej oraz prawdopodobieństw rozrodu i śmierci osobnika. Populację – zbiór osobników żyjących w danej chwili – najwygodniej jest zaprogramować jako listę, choć na logikę populacja jest zbiorem osobników i jako zbiór powinna być programowana. Z doświadczenia jednak wiem, ze symulacja programu, w którym populacja w chwili t i w chwili t+1 są listami jest szybsza niż program, gdzie są one zbiorami.
class stanosobnika:
NR=0
populacja=[]
|
Program, w którym zdefiniowano najprostszą populację i założono, że w każdym kroku czasowym każdy z żyjących osobników może się rozrodzić z prawdopodobieństwem 0.5 oraz umrzeć z prawdopodobieństwem 0.5 wygląda następująco:
from random import random
class stanosobnika:
NR=0
populacja1=[]
N0=100
pr=0.5
ps=0.5
czas=100
lpow=10
for pow in range(1,lpow+1):
populacja=[]
for i in range(N0):
osob=stanosobnika()
osob.NR=i
populacja.append(osob)
N=N0
ostnr=N0
print(pow,0,N)
for t in range(1,czas+1):
n=0
for i in range(N):
osob=populacja[i]
if random()<pr:
potom=stanosobnika()
potom.NR=ostnr+1
ostnr=ostnr+1
populacja1.append(potom)
n=n+1
if random()<ps:
pass
else:
populacja1.append(osob)
n=n+1
N=n
if N>100000:
break
populacja=populacja1
populacja1=[]
print(pow,t,N)
|
Należy zwrócić uwagę, że osobniki nowonarodzone w czasie [t, t+1) nie podlegają w tym kroku czasowym selekcji, nie umierają. Jest to model pasujący do rzeczywistych badań populacji wykonywanych co jakiś czas, w których osobników urodzonych i zmarłych między badaniami nie rejestruje się i w ogóle nie uwzględnia w analizach demograficznych.
Górne ograniczenie na wielkość populacji jest ważne z praktycznego punktu widzenia. Bardzo łatwo jest zaprogramować populację, której liczebność wzrasta w takim tempie, że na jej przetworzenie nie wystarczy zasobów żadnego komputera. To czasem może się zdarzyć przez wstawienie omyłkowej wartości za któryś z parametrów modelu.
Wyniki symulacji najprostszej populacji i ich analiza
Opisany kod wypisuje liczebność populacji w IDLE Pythona i niewiele z tego wynika. Pokazuje wyłącznie liczebność populacji zazwyczaj zmieniającą się w czasie. Znacznie lepiej zapisać to w pliku tekstowym, który można później zaimportować do programu R lub do arkusza kalkulacyjnego, zrobić wykresy wygenerowanych dynamik. Nie tylko to można analizować nie zmieniając modelu. Na przykład:
- Liczby zmarłych w kolejnych krokach czasowych.
- Liczby nowonarodzonych w kolejnych krokach czasowych.
- Długość życia osobników.
- Krotność podchodzenia do rozrodu.
- Procentowy udział potomków kolejnych osobników populacji początkowej.
Aby wykonać te analizy należy gromadzić w plikach tekstowych dane o wieku osobników w chwili jego śmierci, dane o liczbie rozrodów osobników w chwili jego śmierci, dane o liczbie potomków osobników populacji początkowej w każdym kroku czasowym. Wymaga to modyfikacji programu, choć raczej nie uznalibyśmy tego procederu, jako zmianę modelu populacji (tak badania terenowe i laboratoryjne rzeczywistej populacji nie powodują zmiany samej populacji).
W teorii populacji specjalne miejsce mają obok analiz dynamiki liczebności populacji, także analiza długości życia osobników (w postaci rozkładu tej wielkości) oraz analiza struktury populacji względem pochodzenia od konkretnych osobników populacji początkowej. Wymaga to następujących zmian programu:
from random import random
class stanosobnika:
NR=0
WIEK=1
PRZODEK=0
populacja1=[]
N0=100
pr=0.5
ps=0.5
czas=100
lpow=10
tekst1='Powt, t, N'
for i in range(1,N0+1):
tekst1 = tekst1 + "," + 'N' + str(i)
tekst1=tekst1 + "\n"
wyniki1 = open('wyniki1.txt','w')
tekst2='Powt, czassmierci, Nrosob, Dlzycia \n'
wyniki2 = open('wyniki2.txt','w')
for pow in range(1,lpow+1):
populacja=[]
potomki=[]
for i in range(N0):
osob=stanosobnika()
osob.NR=i
osob.WIEK=1
osob.PRZODEK=i
populacja.append(osob)
potomki.append(1)
N=N0
ostnr=N0
t=0
print(pow,0,N)
tekst1=tekst1 + str(pow) + ", " + str(t) + ", " + str(N)
for j in range(N0):
tekst1=tekst1 + "," + str(potomki[j])
tekst1 = tekst1 + "\n"
for t in range(1,czas+1):
n=0
for i in range(N):
osob=populacja[i]
osob.WIEK=osob.WIEK+1
if random()<pr:
potom=stanosobnika()
potom.NR=ostnr+1
potom.WIEK=0
potom.PRZODEK=osob.PRZODEK
ostnr=ostnr+1
populacja1.append(potom)
n=n+1
if random()<ps:
tekst2 = tekst2 + str(pow) + "," + str(t) + ","
tekst2 = tekst2 + str(osob.NR) + "," + str(osob.WIEK) + "\n"
else:
osob.WIEK=osob.WIEK+1
populacja1.append(osob)
n=n+1
N=n
if N>100000:
break
for j in range(0,N0): potomki[j]=0
for i in range(0,N):
osob=populacja1[i]
potomki[osob.PRZODEK]=potomki[osob.PRZODEK]+1
populacja=populacja1
populacja1=[]
print(pow,t,N)
tekst1=tekst1 + str(pow) + ", " + str(t) + ", " + str(N)
for j in range(N0): tekst1=tekst1 + "," + str(potomki[j])
tekst1=tekst1 + "\n"
open('wyniki1.txt', 'a').write(tekst1)
wyniki1.close()
open('wyniki2.txt','a').write(tekst2)
wyniki2.close()
|
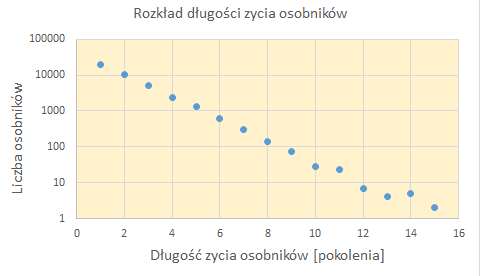
Program tworzy dwa pliki tekstowe, w którym zapisywane są informacje o strukturze populacji w każdym powtórzeniu i kroku czasowym oraz o długości życia osobników wszystkich, które zmarłych. Ich opracowanie ma taki sam charakter, jak opracowanie tego typu danych dotyczących rzeczywistych populacji. Zmiany struktury populacji z pokolenia na pokolenie bada się głównie rysując obok siebie wykresy słupkowe, w których każdy słupek podzielony jest na odcinki proporcjonalne do ilości osobników należących do danej klasy w strukturze (tu mających tego samego przodka z populacji początkowej). Natomiast długość życia osobników analizuje się głównie tworząc rozkład tej zmiennej, przy czym oś pionową (liczby osobników żyjących daną liczbę kroków czasowych) logarytmuje się.
Efekty obserwowane po analizie struktury populacji względem pochodzenia od osobników populacji początkowej mają wiele wspólnego z procesem stochastycznym Galtona-Watsona, natomiast rozkład długości życia osobników z prawem umieralności Gompertza.
Model dynamiki liczebności najprostszej populacji – model nieobiektowy
Gdy rozważania skracamy do dynamiki liczebności najprostszej populacji to możemy zrezygnować z obiektowości. Wykreślając z pierwszego programu wszystkie instrukcje przetwarzające obiekty uzyskujemy prosty, szybki program dający takie same wyniki.
from random import random
N0=100
pr=0.5
ps=0.5
czas=100
lpow=10
tekst=''
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
N=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
for t in range(1,czas+1):
n=0
for i in range(N):
if random()<pr: n=n+1
if random()<ps: pass
else: n=n+1
N=n
if N>100000: break
tekst = tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Dość łatwo sprawdzić, że program ten powstał wyłącznie przez wykreślenie z kodu programu symulującego najprostszą populację wszystkiego, co dotyczyło klasy jaką był osobnik. Program ten wyprowadza dynamiki liczebności takie same jak poprzedni w tym sensie, że prawdopodobieństwa pojawienia się każdej z nich są identyczne w obu programach. Jest krótszy, nieco szybszy i tworzenie osobników oraz populacji wirtualnych wydaje się bezcelowe.
Ten program jednak nie zasługuje już na miano modelu populacji. Jest to bowiem model dynamiki liczebności najprostszej populacji. Można jeszcze poprzez dodatkowe instrukcje wyliczać liczby osobników rozradzających się i zmarłych w kolejnych krokach czasowych. Można prowadzić symulacje do chwili wymarcia populacji i analizować długość trwania tej populacji (zwanej też czasem ekstynkcji) w zależności od parametrów N0, pr i ps. Ale analiz dotyczących długości życia osobników, lub struktury populacji względem pochodzenia od wspólnego przodka, już nie da się za jego pomocą wykonać.
Dla modelu dynamiki liczebności populacji można wykonać proste analizy probabilistyczne. Przy stałym prawdopodobieństwie rozrodu i śmierci możemy wyliczyć, jakie jest prawdopodobieństwo, że populacja licząca k osobników w chwili t, w chwili t+1 będzie składała się z n osobników. Będzie to suma prawdopodobieństw dla wszystkich możliwych urodzeń r osobników, że urodziło się r osobników i zmarło x osobników, tak że k+r-x=n (czyli x=k+r-n). Zjawiska urodzeń i śmierci tworzą dwa schematy Bernoulliego (sukces z prawdopodobieństwem pr, porażka z prawdopodobieństwem 1-pr, sukces z prawdopodobieństwem ps, porażka z prawdopodobieństwem 1-ps). Prawdopodobieństwa urodzin R osobników i śmierci S osobników dane są wzorami dwumianowymi z parametrami N, pr i N, ps. Innymi słowy można w każdym kroku czasowym wylosować z rozkładu dwumianowego liczbę R osobników, które się rozrodziły i liczbę S osobników, które zmarły i wyliczyć liczebność w kroku następnym ze wzoru N = N + R – S.
from random import random
def losujbinom(N,p):
alfa = random()
K = 0
sumaprawd = (1-p)**N
prawd = (1-p)**N
while sumaprawd<alfa:
K=K+1
prawd=(N-K+1)/K*p/(1-p)*prawd
sumaprawd=sumaprawd+prawd
return K
N0=100
pr=0.5
ps=0.5
czas=100
lpow=10
tekst=''
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
N=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
for t in range(1,czas+1):
R = losujbinom(N,pr)
S = losujbinom(N,ps)
N = N + R - S
if N>100000: break
print(pow,t,N)
tekst = tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Taki program tworzy nam ciąg liczbowy na podstawie podwójnego losowania liczb z rozkładów dwumianowych. Można go zapisać w postaci łańcucha stochastycznego:
N0 → N1 → N2 → . . . → Nt
W łańcuchu tym N1, N2, … są zmiennymi losowymi z prawdopodobieństwem przejścia od liczebności Nt=k do Nt+1=n równym:
Prawdopodobieństwo to zależy wyłącznie od stałych pr i ps oraz wartości liczebności Nt. Łańcuchy stochastyczne o takiej własności nazywamy łańcuchami Markowa. Odgrywają one ważną rolę w biologii.
Zadanie pierwsze dla studentów
Zostały podane trzy kody źródłowe symulujące dynamikę liczebności najprostszej populacji (pomijam kod rozszerzony o analizę wieku i struktury populacji). Każdy z nich zapisuje te wygenerowane dynamiki w pliku wyniki.txt i sposób zapisu wyników jest w nich taki sam, więc nie wpływa na szybkość symulacji, czy mówiąc dokładniej tak samo spowalnia symulację. Spodziewamy się, że ostatni z programów działa najszybciej. Należy to sprawdzić eksperymentalnie. Przy okazji należy sprawdzić czy parametry N0, pr i ps wpływają na czas symulacji (bo czas = liczba kroków czasowych w jakich symuluje się populacja i lpow – liczba powtórzeń symulacji robią to z definicji).
- Należy wpisać na początku i końcu każdego z programów funkcje odczytujące aktualny czas (import time, print(time.time), itd).
- Należy wstawić z czas i lpow odpowiednio duże liczby, by uzyskać widoczne różnice.
- Zastosować na początek parametry pr=0.5, ps=0.5, N0=50 i wyliczyć czas trwania symulacji dla każdego z kodów źródłowych.
- Zwiększyć N0 do 100 i ponownie wyliczyć czasy trwania symulacji
- Systematycznie zwiększać N0 aż do 1000 i zapisywać czasy trwania symulacji.
- Przedstawić stosowną tabelę.
- Odpowiedzieć na pytanie, dlaczego w miar wzrostu N0 czas symulacji rośnie?
- Ustalić N0 (nie za małe, nie za duże) i zmieniać pr i ps na liczby 0.1, 0.1 potem 0.2, 0.2 itd., do 0.9, 0.9. Za każdym razem wyliczać czas symulacji. Stworzyć kolejną tabelę. Czy wszystkie wyniki są takie same? Jeżeli nie, to dlaczego?
Zadanie drugie dla studentów
Zapoznać się z kodem symulującym najprostsza populację z analizą wieku osobników i strukturę populacji związaną z pochodzeniem od konkretnego osobnika populacji początkowej. Wyniki symulacji zapisywane są w dwóch plikach tekstowych “wyniki1.txt” – charakterystyki stanu populacji w kolejnych krokach czasowych i “wyniki2.txt” – charakterystyki osobników w chwili śmierci. W tym zadaniu studenta interesował będzie plik wyniki2.txt, w którym charakteryzowane są osobniki w chwili śmierci. Choć wydaje się, że osobniki w tej populacji są takie same, to jednak ustalane losowo ich historie życia różnią się od siebie. Zadaniem studenta będzie charakterystyka zbiorcza osobników, które wystąpiły w populacji w arkuszu kalkulacyjnym Excel albo Calc.
- Wykonać symulację dla parametrów pr=0.5, ps=0.5, N0=100, czas=100, lpowt=10.
- Otworzyć arkusz kalkulacyjny.
- Kliknąć na otwórz, wybrać pliki tekstowe. Pojawi się wtedy możliwość otwarcia pliku “wyniki2.txt” tak, by odpowiednie dane były w osobnych kolumnach. Wystarczy jako separator kolumn odhaczyć spację.
- Uszeregować osobniki według Powt oraz Nrosob i zobaczyć ile osobników przewinęło się przez populację w czasie 1000 kroków czasowych (Największy numer w Nrosob).
- Jak bardzo poszczególne powtórzenia mogą się różnić tym parametrem od siebie (uwaga, gdy dla 1000 kroku czasowego nie ma osobników, to populacja wymarła).
- Uszeregować osobniki według Powt i Dlzycia. Wykonać rozkłady długości życia (czy określić wartości funkcji: k → liczba osobników żyjacych k dni dla wszystkich k) i zobrazować to graficznie. Przejść na częstość życia (czyli liczbę osobników żyjacych k dni podzielić przez liczbę wszystkich osobników) i zlogarytmować oś pionową. Nałożyc na jeden wykres wyniki dla powtórzeń symulacji. Czy pokryły sie one?
- Wykonać symulację dla parametrów pr=0.1, ps=0.1, N0=100, czas=100, lpowt=10. i w podobny sposób opracować wyniki związane z długościa życia
- Wykonać symulację dla parametrów pr=0.9, ps=0.9, N0=100, czas=100, lpowt=10. i w podobny sposób opracować wyniki związane z długościa życia.
- Czy parametr N0 ma wpływ na te wyniki?
Zadanie trzecie dla studentów
Zapoznać się z kodem symulującym najprostsza populację z analizą wieku osobników i strukturę populacji związaną z pochodzeniem od konkretnego osobnika populacji początkowej. Wyniki symulacji zapisywane są w dwóch plikach tekstowych “wyniki1.txt” – charakterystyki stanu populacji w kolejnych krokach czasowych i “wyniki2.txt” – charakterystyki osobników w chwili śmierci. Symulacje należy wykonać dla N0=20, pr=0.5, ps=0.5 i czasowi równemu 1000 albo dłuższemu. Dopisać instrukcje kończąca pętle czasu, gdy już tylko potomkowie jednego osobnika z populacji początkowej pozostają w populacji (lista “potomki” ma już tylko jeden element niezerowy). Należy je opracować w arkuszy kalkulacyjnym Excel albo Calc.
- Otworzyć arkusz kalkulacyjny.
- Kliknąć na otwórz, wybrać pliki tekstowe. Pojawi się wtedy możliwość otwarcia pliku tak, by odpowiednie dane były w osobnych kolumnach. Wystarczy jako separator kolumn odhaczyć spację.
- Wykonać wykres struktury populacji względem pochodzenia od odpowiedniego przodka.
- Policzyć i ile osobników populacji początkowej miało potomków po 1,2,3,…,t-tym kroku czasowym.
- Zmienić N0 na 50, a później na 100 i ponownie wykonać symulacje oraz analizy.
- Zmienić pr na 0.1 i ps na 0.1 i ponownie wykonać analizy.
- Zmienić pr na 0.9 i ps na 0.9 i ponownie wykonać analizy.
- Jak parametry modelu wpływają na model.
- Omawiając wyniki zobaczyć jak się ma wykonany model do procesu Galtona-Watsona.