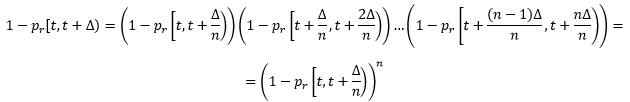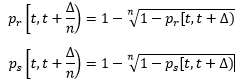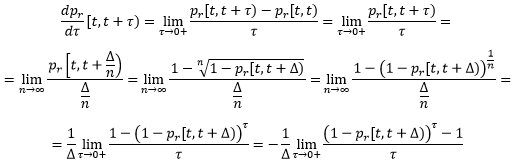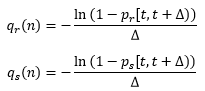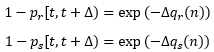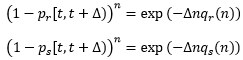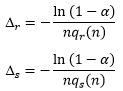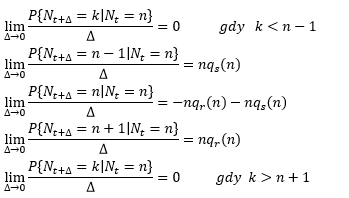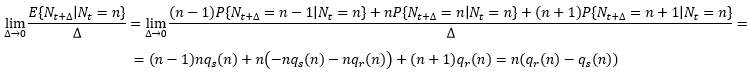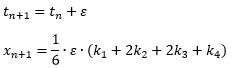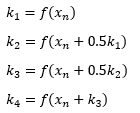Model najprostszej populacji w czasie ciągłym
Najprostszy model populacji w czasie ciągłym
Ze względu na podręczniki ekologii i standardowe modele różniczkowe (model logistyczny, modele drapieżnik ofiara, itp.), analizowanie populacji w czasie dyskretnym wydaje się to być pewnym ograniczeniem. W tym rozdziale pokażę, jak utworzyć model populacji w czasie ciągłym, bo nie jest prawdą, że nie jest to możliwe. Co więcej, proces stochastyczny opisujący dynamiki liczebności generowane w tym modelu, jest identyczny z dobrze znanym procesem urodzin i śmierci, a krzywa przewidywana wyprowadzona w analogiczny sposób, jak to robi się w dla modeli w czasie dyskretnym, pokrywa się z modelem logistycznym. Jednak zastosowanie tego modelu jest ograniczone wielokrotnie dłuższym czasem symulacji.
Manipulowanie czasem
Ludzie tak bardzo przywykli do addytywnych wielkości, że wyobrażają sobie iż w dwa razy dłuższym czasie, częstość zdarzeń (i prawdopodobieństwo) będzie dwa razy większe. Jest to nieprawda. Prawdopodobieństwa nie są addytywne (no bo co, gdyby w jednostce czasu prawdopodobieństwo zdarzenia było równe 0.6; czy w dwóch jednostkach byłoby równe 1.2?).
Rozważmy prawdopodobieństwo śmierci konkretnego osobnika ps(N) w modelu zagęszczeniozależnym najprostszej populacji w czasie [t, t+1). Jeżeli osobnik urodził się w chwili t, reguła modelowania mówi, że przeżywa do chwili t+1. Przy liczeniu osobników modelu pomija się te, które urodziły się i zmarły w czasie [t,t+1), tak jak to zazwyczaj robi się przy okresowych kontrolach populacji. Okres [t+1, 1) osobnik przeżywa z prawdopodobieństwem 1-ps(Nt+1). Okres [t+2, t+3) przeżywa z prawdopodobieństwem 1-ps(Nt+2). Okres [t+3, t+4) przeżywa z prawdopodobieństwem 1-ps(Nt+3), itd. Zdarzenia przeżywania w krokach czasowych [t+1,t+2), [t+2,t+3), [t+3, t+4) są niezależne, zatem prawdopodobieństwo, że osobnik przeżyje czas [t,t+4) lub dłuższy, jest równe:
Prawdopodobieństwa zdarzeń nie są addytywne, ale prawdopodobieństwa braków zdarzeń są multiplikatywne.
Rozważmy teraz taką sytuację. Populacja ma N osobników i czekamy na śmierć jednego z nich, a czas liczymy w kolejnych jednostkach, np. w godzinach. Śmierć może nastąpić w każdej minucie, sekundzie, milisekundzie, jednym słowem w każdej chwili wyrażanej dowolna liczbą rzeczywistą. Dopóki liczebność populacji będzie równa N, będzie ono stałe w odcinkach czasu o jednakowej długości. Jest jednak oczywiste, że prawdopodobieństwo śmierci osobnika w krótszym czasie będzie mniejsze niż w dłuższym obejmującym ten krótszy czas. Niech t+Δ będzie momentem, w którym populacja licząca n osobników zmienia swoją liczebność. Niech pr[t,t+Δ) będzie prawdopodobieństwem rozrodu a ps[t,t+Δ) śmierci osobnika w czasie równym [t,t+Δ). Podzielmy czas Δ na n równych odcinków czasowych. W tym czasie prawdopodobieństwa rozrodu i śmierci są stałe, zatem:
Analogicznie:
Wynika stąd, że:
Są to wzory, którymi ekolodzy powinni się posługiwać, gdy częstość zdarzeń (np. śmierci) wyznaczoną eksperymentalnie np. w czasie 5 dni, chcą przeliczyć na 1 dzień (rzecz powszechnie robiona w badaniach drobnych ssaków i równie powszechnie robiony jest błąd – dzielenie przez 5). Nas jednak interesuje przejście z czasem do nieskończenie krótkiego odcinka czasowego, by móc modelować w czasie ciągłym. Ponieważ funkcje: τ→pr(t,t+τ) oraz τ→pr(t,t+τ) rosną od 0 do 1, to granice powyższych funkcji n→∞ są równe 0.
Nie są one interesujące. Ale pochodne prawostronne tych funkcji Δ→p[t,t+Δ) w punkcie Δ=0 zmierzają do konkretnych, większych od zera wielkości. Można je wyliczyć posługując się zależnościami takimi jak: p(t,t+0)=0 oraz limn→∞f(1/n)=limx→0f(x) dla funkcji f(x) ciągłej prawostronnie w 0. Zatem:
Granica występująca w ostatnim wyrażeniu jest pochodną funkcji (1-pr(t+Δ))x w punkcje x=0. A ponieważ pochodna funkcji ax jest równa ln(a)ax i a0=1, to ostatecznie:
dla dowolnego czasu Δ, takiego, że w okresie [t,t+Δ) populacja nie zmienia swojej liczebności.
Analogicznie:
W obu wzorach wewnątrz logarytmu jest liczba mniejsza od 1, zatem jej logarytm jest ujemny. Znak minus przed ilorazem gwarantuje nam, że pochodne w zerze wyprowadzonych wzorów są dodatnie.
Ostatnia wielkość znajduje się w niektórych podręcznikach ekologii, np. w dodatku w podręczniku Krebsa pt. “Ekologia”. Nazwana została śmiertelnością punktową (angl. instantaneous mortality rate). W teorii procesów stochastycznych w czasie ciągłym przyjęto takie wielkości nazywać intensywnościami prawdopodobieństwa (angl. intensity of the probability) i taka terminologia będzie stosowana w dalszej części tego rozdziału, by jej nie zmieniać w podrozdziale o procesie urodzin i śmierci. Dwa ostatnie wzory pokazują, jak wyliczyć intensywność prawdopodobieństwa rozrodu i śmierci w oparciu o eksperyment pokazany w rozdziale 6 i bazę danych postaci:
| Liczebność | Liczba rozradzających się |
Liczba zmarłych |
| 20 | 15 | 3 |
| 30 | 22 | 5 |
| 40 | 23 | 12 |
| 50 | 15 | 19 |
| 60 | 16 | 43 |
| 70 | 8 | 51 |
| 80 | 9 | 67 |
Gdy okres uzyskania tych danych wynosi Δ, to zamiast liczyć częstości zdarzeń, wylicza się -ln(1-R/N)/Δ oraz -ln(1-S/N)/Δ, gdzie R jest liczbą rozradzających się, a S liczbą zmarłych. Następnie wylicza się odpowiednią regresję między liczebnością populacji, a intensywnościami prawdopodobieństwa z rodzin funkcji nieujemnych.
Intensywności prawdopodobieństwa rozrodu i śmierci, to tempo zmian prawdopodobieństwa rozrodu i śmierci. Zatem mają się tak do samego prawdopodobieństwa, jak prędkość do przebytej drogi. Prawdopodobieństwo jest wielkością niemianowaną, zatem intensywności prawdopodobieństwa będą liczone w jednostkach “osobników/jed.czasu” albo “zdarzeń/jedn. czasu”. Na przykład tempo rozrodu równe 11 osobników/rok, tempo umierania równe 22.5 zgonów/tydzień itd. Przeliczanie na inną jednostkę czasu jest takie samo, jak we wszystkich wielkościach fizycznych. Przykładowo 0.6 zdarzeń/doba=1/40 zdarzeń/godz. = 1/240 zdarzeń/min. Jednocześnie zdarzeń/doba = 213.6 zdarzeń/rok. Intensywności prawdopodobieństwa mogą być większe od 1. (to tak, jak możliwość uzyskania 100 km/godz. bez potrzeby jechania przez godzinę drogi o długości 100 km). Nie mogą być jednak mniejsze od 0, bo są pochodnymi funkcji Δ→p(t,t+Δ), która nie może maleć.
Najprostszy obiektowy model populacji w czasie ciągłym
W modelu najprostszej populacji w czasie ciągłym zakładamy, że intensywności prawdopodobieństwa są funkcją liczebności populacji:
Innymi słowy zakładamy istnienie funkcji qr(n) i qs(n) nie zależnych od czasu, a tylko od liczebności. Argumenty za takim założeniem są takie same jak dla modelu w czasie dyskretnym. Intensywność prawdopodobieństwa śmierci i rozrodu zależą od ilości zasobów przypadających na jednego osobnika, a ilość zasobów przypadających na jednego osobnika zależy od liczebności populacji. Innymi słowy są to pewne regresje nieliniowe, wybrane z rodziny funkcji nieujemnych, między liczebnością populacji a intensywnościami prawdopodobieństwa rozrodu i śmierci wyliczonymi eksperymentalnie.
Niech w chwili t populacji składa się z n osobników, czyli Nt=n. Niech Δ będzie czasem takim, że w przedziale [t,t+Δ) żaden z osobników nie rozrodzi się i nie umrze. Wtedy zgodnie z wyprowadzonymi wcześniej wzorami:
Wyliczając z niego prawdopodobieństwo, że wybrany osobnik nie rozrodzi się oraz nie umrze w okresie [t,t+Δ), otrzymujemy:
Prawdopodobieństwo, że żaden z n osobników nie rozrodzi się i nie umrze w tym czasie jest równe:
gdyż dla różnych osobników prawdopodobieństwa te są niezależne. Prawdopodobieństwa:
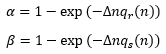 można nazwać prawdopodobieństwami zdarzeń które potencjalnie mogą wystąpić w populacji w czasie [t,t+Δ), przy czym wystąpi to zdarzenie, któremu odpowiadający czas Δ będzie krótszy. Oznacza to, że możemy wylosować liczby α i β z przedziału [0,1]. Następnie wyliczyć:
można nazwać prawdopodobieństwami zdarzeń które potencjalnie mogą wystąpić w populacji w czasie [t,t+Δ), przy czym wystąpi to zdarzenie, któremu odpowiadający czas Δ będzie krótszy. Oznacza to, że możemy wylosować liczby α i β z przedziału [0,1]. Następnie wyliczyć:
i to zdarzenie się zdarzy najpierw w populacji, dla którego czas Δ będzie krótszy. W modelu trzeba będzie jeszcze wylosować osobnika, któremu to się zdarzy. Ponadto, kiedy liczebność populacji jest równa 0 to zdarzeniom tym przypisujemy czas nieskończony (Δr=∞ i Δs=∞), a w programie maksymalny, co kończy symulację.
Program stosujący te reguły, z liniowymi formułami dla funkcji qr(n) i qs(n), wygląda następująco:
#Symulator najprostszej populacji w czasie ciągłym - model obiektowy
from random import random,randrange
from math import log
class stanosobnika:
NR=0
populacja=[]
#Parametry do podmiany
N0=10;ar=-0.005;br=1;ass=0.005;bs=0;
czas=100;lpow=5
tekst=''
wyniki = open('wyniki.txt', 'w')
#pętla powtórzeń
for pow in range(1,lpow+1):
for i in range(N0):
osob=stanosobnika()
osob.NR=i
populacja.append(osob)
N=N0
ostnr=N0
t=0
tekst=tekst+str(pow)+", "+str(t)+", "+str(N)+"\n"
#pętla czasu
while (t< czas and t<100000):
osob=populacja[randrange(N)]
qr=ar*N+br
qs=ass*N+bs
if (qr<0 or qs<0):pass
if (N>0): Deltar=-log(1-random())/(N*qr)
else: Deltar=czas
if (N>0): Deltas=-log(1-random())/(N*qs)
else: Deltas=czas
if Deltar<=Deltas:
potom=stanosobnika()
potom.NR=ostnr+1
ostnr=ostnr+1
populacja.append(potom)
N=N+1
t=t+Deltar
if (Deltas<Deltar):
populacja.remove(osob)
N=N-1
t=t+Deltas
if N>100000:
break
print(pow,t,N)
tekst = tekst+str(pow)+", "+str(t)+", "+str(N)+"\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
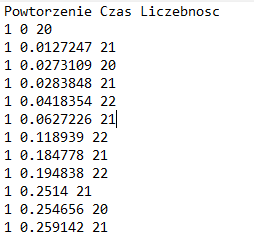
Wykonanie podanego programu powoduje powstanie pliku tekstowego, którego początek wygląda podobnie do:
Czas biegnie nierównomiernie od zdarzenia do zdarzenia. Po zmianach liczebności widać, kiedy doszło do zdarzenia rozrodu, a kiedy śmierci. Powstały plik jest bardzo długi, a w kolejnych powtórzeniach osie czasu nie pokrywają się. W Excelu trzeba wykonywać wykresy dla każdego powtórzenia osobno, a potem nakładać je na siebie (uaktywnia się pierwszy wykres, wkłada do pamięci podręcznej Ctrl+C, uaktywnia drugi wykres i klika Ctrl+V).
Pokazany model ma kilka wariantów symulujących takie same populacje. Po pierwsze w pokazanym modelu losuje się osobnika i dla niego zakłada, że jest to pierwszy osobnik dla którego zajdzie jedno ze zdarzeń: rozród albo śmierć. To samo daje obliczenie najpierw, który czas wyjdzie krótszy – rozród jakiegoś osobnika lub śmierć jakiegoś osobnika i potem wylosowanie go. To zwykła zmiana kolejności instrukcji. Można byłoby także brać po kolei każdego osobnika, losować dla niego dwie liczby z przedziału [0,1], wyznaczać dla niego czas po jakim rozrodzi się i czas po jakim umrze ze wzorów tr=-ln(1-α)/qr(n)) i ts=-ln(1-α)/qs(n)) i znajdywać najmniejszą z pośród 2n liczb: tr i ts, co określi osobnika i zdarzenie, które jego będzie dotyczyć. Ten model wymaga dodatkowej pętli. Jest zatem wyraźnie wolniejszy, ale pokazuje jak postępować, gdy osobniki są bardziej skomplikowane i intensywności prawdopodobieństwa zdarzeń rozrodu i śmierci dla poszczególnych osobników nie są jednakowe, np. są funkcją dwuargumentową i zależą od liczebności populacji i od wieku osobników.
Nieobiektowy model dynamiki liczebności najprostszej populacji w czasie ciągłym
Podobnie jak dla modelu w czasie dyskretnym, poprzez wykreślenie wszystkiego co jest obiektem (osobnika, populacji) i funkcji z nimi związanych, powstaje szybszy model tworzący takie same i tak samo prawdopodobne dynamiki liczebności w czasie ciągłym. Wygląda on następująco:
#Model najprostszej populacji w czasie ciągłym - model nieobiektowy
from random import random,randrange
from math import log
#Parametry do podmiany
N0=10;ar=-0.005;br=1;ass=0.005;bs=0;
czas=100;lpow=5
tekst=''
wyniki = open('wyniki.txt', 'w')
#pętla powtórzeń
for pow in range(1,lpow+1):
N=N0
ostnr=N0
t=0
tekst=tekst+str(pow)+", "+str(t)+", "+str(N)+"\n"
#pętla czasu
while t < czas:
qr=ar*N+br
qs=ass*N+bs
if (qr<0 or qs0): Deltar=-log(1-random())/(N*qr)
else: Deltar=czas
if (N>0): Deltas=-log(1-random())/(N*qs)
else: Deltas=czas
if Deltar<=Deltas:
N=N+1
t=t+Deltar
if (Deltas100000:
break
print(pow,t,N)
tekst = tekst+str(pow)+", "+str(t)+", "+str(N)+"\n"
if N==0: break
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Program ten można nazwać modelem dynamiki liczebności najprostszej populacji w czasie ciągłym. Nie da się uogólniać, gdy komplikujemy i różnicujemy osobniki, a zwłaszcza gdy intensywności prawdopodobieństwa rozrodu lub śmierci zależą od cech osobników.
Dynamika liczebności najprostszej populacji w czasie ciągłym jako proces urodzin i śmierci
Dynamika liczebności symulowana za pomocą intensywności prawdopodobieństw jest procesem stochastycznym. Spełnia wszystkie warunki definicji procesu stochastycznego, którego definicja podana była w rozdziale 8. Ma on także własność Markowa bo prawdopodobieństwa przyszłych zdarzeń zależą tylko od stanu populacji czyli jej liczebności w czasie teraźniejszym.
Procesy stochastyczne w czasie ciągłym oznacza się zazwyczaj jako (Nt)t∈[0,∞) lub po prostu (Nt). Samo Nt jest zmienną losową, której wartościami są liczebności.
Proces Markowa w czasie ciągłym posiada odpowiednik macierzy stochastycznej – macierz intensywności, zwana też macierzą przejścia (angl. intensity matrix , state-transition matrix). Zawiera ona intensywności prawdopodobieństw warunkowych P{Nt+ε=k|Nt=n} czyli liczby:
Wyliczymy je dla naszego modelu.
Działanie programu wyklucza zaistnienie dwóch zdarzeń w tej samej chwili. Przejścia z n na k<n-1 i z n na k>n+1 są niemożliwe czyli:
P{Nt+Δ=n-1|Nt=n} jest prawdopodobieństwem śmierci jakiegoś osobnika. Korzystając ze wzoru pokazanego na początku drugiego podrozdziału mamy:
Podobnie:
Najdłużej trwa wyprowadzenie wzoru na P{Nt+Δ=n|Nt=n}. Funkcja Δ→P{Nt+Δ=n|Nt=n} jest malejąca i spodziewamy się wartości ujemnej pochodnej w zerze. Jednocześnie:
P{Nt+Δ=n-1|Nt=n}+P{Nt+Δ=n|Nt=n}+P{Nt+Δ=n+1|Nt=n}=1
Stąd:
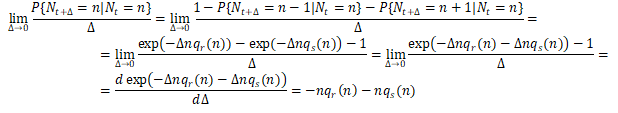 Podsumowując wyprowadziliśmy wszystkie wzory na intensywności prawdopodobieństw przejścia ze stanu n do stanu jaki może się pojawić w najbliższej przyszłości. Powstaje macierz, w której prawie wszystkie wyrazy są równe 0, poza wyrazami ujemnymi na przekątnej i dodatnimi w pasach równoległych do przekątnej i z nią sąsiadujących. Dokładnie to:
Podsumowując wyprowadziliśmy wszystkie wzory na intensywności prawdopodobieństw przejścia ze stanu n do stanu jaki może się pojawić w najbliższej przyszłości. Powstaje macierz, w której prawie wszystkie wyrazy są równe 0, poza wyrazami ujemnymi na przekątnej i dodatnimi w pasach równoległych do przekątnej i z nią sąsiadujących. Dokładnie to:
Proces stochastyczny zdefiniowany przez taką macierz intensywności jest znany w biologii teoretycznej pod nazwą procesu urodzin i śmierci (angl. birth and death process). Omawiany jest w wielu podręcznikach zarówno matematycznych jak i ekologicznych. Często wielkość nqr(n) oznacza się symbolem μn, a wielkość nqs(n) oznacza się λn i nazywa się je współczynnikami urodzin (birth rate) i śmierci (death rate) odpowiednio. Sam proces definiuje się najczęściej za pomocą grafów, które słabo się kojarzą z populacją (jest to wtedy proces liczbowy typu: dodaj lub odejmij 1 od poprzedniego wyniku w losowo ustalanym czasie). Poza tym, prawdopodobieństwa rozrodu pr(n) i śmierci ps(n) osobnika różnią się n-krotnie od współczynnika narodzin μn i śmierci λn, o czym należy pamiętać czytając teoretyczne rozważania o tym procesie. Dotyczą one rozrodu i śmierci każdego pojedynczego osobnika, a μn i λn dotyczą zdarzenia dla jakiegokolwiek osobnika w populacji.
W teorii procesów stochastycznych, każdą macierz liczbową, w której poza przekątną są wyrazy dodatnie, na przekątnej ujemne i suma wyrazów w każdym wierszu (w orientacji matematycznej), kolumnie (gdy wstawimy tę macierz do układu współrzędnych) jest równa 0. Dla każdej takiej macierzy możemy utworzyć program symulujący realizacje procesu stochastycznego. Jest to dość powolny, ale jednak uniwersalny program symulujący procesy stochastyczne w czasie ciągłym mające własność Markowa.
Warunkowe wartości oczekiwane przyrostu liczebności populacji i przewidywana dynamika liczebności
Macierz intensywności utworzona dla procesu urodzin i śmierci jest teoretycznie nieskończona. Nawet włożona do układu współrzędnych nie wygląda ciekawie. Ma tylko wartości na przekątnej (ujemne) i obok niej o 1 element w dół i w górę (dodatnie). Jednak pozwala ona na wyliczenie warunkowych wartości oczekiwanych tempa zmian liczebności populacji po chwili t, pod warunkiem, że w chwili t była ona równa n. Jest to wielkość:
Prawa strona tego równania może być traktowana jako funkcja zmiennej rzeczywistej, jeżeli tylko pr(n) i ps(n) były wyliczane jako regresje. Ma wtedy sens rozważanie funkcji zmiennej rzeczywistej postaci x(pr(x)-ps(x)). Lewa strona powyższego równania, to współczynniki nachylenia stycznych do tej funkcji w punktach będących liczbami całkowitymi. Ale możemy rozważać takie styczne w dowolnych punktach, co prowadzi do równania różniczkowego:
Funkcję, będącą rozwiązaniem tego równania, nazywać będziemy przewidywaną dynamiką liczebności populacji.
Rozwiązywanie równań różniczkowych nie jest domeną biologów, lecz najczęściej wystarczy umieć narysować takie rozwiązanie, wyliczyć stany równowagi, ewentualnie punkty przegięcia. Wszystko to możemy zrobić nie rozwiązując równania różniczkowego, a metody tu stosowane nie są trudne (zwłaszcza, że rachunkami zajmie się komputer).
Stany równowagi równania różniczkowego, to takie wartości x, że dx/dt= 0. Oznacza to, że x(pr(x)-ps(x))=0. Zatem jednym ze stanów równowagi jest x=0, drugim rozwiązanie równania pr(x)=ps(x), co przy stosowaniu wzorów pr(x)=ln(1+exp(arx+br)) i ps(x)=ln(1+exp(asx+bs)) daje zależność x=-(br-bs)/(ar-as)).
Punkty przegięcia funkcji x(t) ma tę własność, że druga pochodna funkcji w tym punkcie jest równa 0. Zatem pierwsza pochodna ma ekstremum. Szukając ekstremów funkcji x→x(pr(x)-ps(x)) znajdziemy wartości punktów przegięcia (nie znajdziemy czasów w jakim te wartości są przyjmowane). Mimo to ułatwia to ich wyliczenie na wykonanym wykresie.
Najpopularniejszą metodą znajdywania wykresów rozwiązań równania różniczkowego jest metoda Rangego-Kutty rzędu 4. Wymaga ona podania wartości funkcji w chwili t=0, ale tego samego wymaga program symulujący populację. Przyjmujemy zatem, że x(0)=n0. Następnie wymaga podania krótkiego okresu czasowego ε do którego odnosić się będzie produkowany ciąg momentów czasowych tn=tn-1+ε oraz ciąg rekurencyjny χn przybliżający funkcję x(t). Zasada definiowana tego ciągu omawiana jest w wielu podręcznikach, a także w Wikipedii.
Mamy równanie różniczkowe x’ = f(x), punkt początkowy x0 oraz krótki odcinek czasowy ε. Tworzymy dwa ciągi rekurencyjne tn i xn zaczynające się w t0=0 i x0. Wtedy:
gdzie:
Bardzo łatwo jest wyliczać takie ciągi w arkuszach kalkulacyjnych.
Zadanie dla studentów
Skopiować kod źródłowy pierwszego programu i dokonać poprawek umożliwiających kompilację (za funkcje fr() wpisać log(1+exp(ar*n+br))) i podobnie za funkcje fs()).
Za N0 przyjąć liczbę AB+10, gdzie AB jest dwucyfrową końcówką numeru indeksu osoby wykonującej ćwiczenie.
Za ar przyjąć -0.001.
Za br przyjąć 0.6.
Za as przyjąć 0.001.
Za bs przyjąć 0.2.
Wykonać 5 powtórzeń symulacji populacji za pomocą pierwszego lub drugiego z podanych programów dla 100 kroków czasowych i wyliczonych parametrów modelu.
Przenieść dane z pliku INFODYN.TXT do Excela.
W niektórych wersjach Excela zapis liczb rzeczywistych jest w systemie europejskim (z przecinkami), tymczasem C++ zapisuje liczby w systemie amerykańskim (z kropkami). W takich programach po wprowadzeniu danych do Excela należy zamienić wszystkie kropki na przecinki na osi czasu (w menu Edit wybrać opcję zamień lub znajdź/zamień, wpisać w odpowiednie miejsca kropkę i przecinek i wybrać opcję zamień wszystko).
Utworzyć 5 wykresów dynamiki liczebności populacji stosując wykres punktowy (z liniami bez znaczników). Każdy ma swoją oś czasu.
Umieścić wykresy na początku pliku i nałożyć na siebie (po uaktywnieniu wykresu wprowadza się go do pamięci przez ctrl+C, uaktywnia wykres docelowy, np. pierwszy i wyprowadza z pamięci: ctrl+V).
Przy standardowych ustawieniach wykresy z różnych powtórzeń powinny zyskać różne kolory. Jeżeli tak się nie stało to kolory powtórzeń zmienić na różne.
Obok, np w kolumnach od L do S, wyliczyć przewidywaną dynamikę liczebności populacji.
- w L1 wpisać “epsilon”
- w M1 wpisać 0.01
- W L2 wpisać “ar”
- W M2 wpisac wartość ar
- W L3 wpisać “br”
- W M3 wpisać wartość br
- W L4 wpisać “as”
- W M4 wpisać wartość as
- W L5 wpisać “bs”
- W M5 wpisać wartość bs
- W N1 wpisać “czas”
- W N2 wpisać 0
- w N3 wpisać =N2+$M$2
- W O1 wpisać “N przewidywana”
- W O2 wpisać liczebność początkową N0
- W O3 wpisać = O2+1/6*$M$1*(P3+2*Q3+2*R3+*S3)
- W P1 wpisać “k1”
- W P2 nic nie wpisać
- W P3 wpisać = O2*(ln(1+exp($M$2*O2+$M$3))-ln(1+exp($M$4*O2+$M$5)))
- W Q1 wpisać “k2”
- W Q2 nic nie wpisać
- W Q3 wpisać = (O2+0.5*P3)*(ln(1+exp($M$2*(O2+0.5*P3)+$M$3))-ln(1+exp($M$4*(O2+0.5*P3)+$M$5)))
- W R1 wpisać “k3”
- W R2 nic nie wpisać
- W R3 wpisać = (O2+0.5*Q3)*(ln(1+exp($M$2*(O2+0.5*Q3)+$M$3))-ln(1+exp($M$4*(O2+0.5*Q3)+$M$5)))
- W S1 wpisać “k4”
- W S2 nic nie wpisać
- W S3 wpisać = (O2+R3)*(ln(1+exp($M$2*(O2+R3)+$M$3))-ln(1+exp($M$4*(O2+R3)+$M$5)))
- Zaznaczyć pola N3:S3
- Przeciągnąć w dół do wiersza 10002
- Zaznaczyć pola czasu i przewidywanej dynamiki (Kolumny N i O)
- Zrobić wykres punktowy (liniowy bez znaczników)
- Nałożyć na wcześniej wykonany wykres dynamik liczebności
- Przewidywana dynamikę pokolorować na czarno i pogrubić
- Podpisać osie, zatytułować.
- Zapamiętać.
Podsumowanie
Najprostsze populacje wirtualne w czasie dyskretnym i ciągłym mają tę wadę, że jej założenia praktycznie nie są spełnione dla żadnej rzeczywistej populacji. Założenie, że prawdopodobieństwa rozrodu i śmierci zależą od ilości zasobów przypadających na osobnika są spełnione prawie zawsze dla wszystkich populacji. Ale drugie założenie, że ilość zasobów przypadających na jednego osobnika zależy od liczebności populacji nie jest spełnione praktycznie nigdy. Ilość zasobów, głównie pokarmu, zmienia się sezonowo i wyczerpuje się przy nadmiernej eksploatacji. Odnawianie się zasobów to na razie mało znana dziedzina i modele operujące ilością zasobów zamiast liczebnością populacji są rzadkie (znam tylko jedna taka pracę autorstwa Adama Łomnickiego).
Zależność od liczebności populacji, nazywana jest zagęszczeniozależnością, gdyż pokutuje powszechna argumentacja, że modele te opisują zagęszczenie populacji nie jej liczebność. Tyle tylko, że zagęszczenie to liczebność podzielona przez stałą i nadal jest to dyskretny zbiór wartości, w dodatku zależny od jednostek pomiaru powierzchni czy objętości. Męczenie matematyków, dlaczego liczebność nie jest całkowita w gruncie rzeczy ma sens, choć ostatecznie można usłyszeć, że chodzi o nieskończoną populację na nieskończonej powierzchni liczonej w nieskończonych jednostkach. W pokazanych rozdziałach pokazano, że niecałkowita liczebność występuje tylko w charakterystykach dynamiki liczebności – oczekiwanej i przewidywanej. Są to bowiem pewne średnie z powtórzeń symulacji, czyli populacji jakie w danych warunkach mogłyby się pojawić. A niecałkowita średnia z liczb całkowitych nikogo nie dziwi. Nie mniej, stosuję nomenklaturę “modele zagęszczeniozależne”, gdyż słowo “liczebnościozależne” nie przechodzi mi przez gardło (uf! ale go napisałam).
W modelach zagęszczeniozależność jest możliwa tylko w specjalnych eksperymentach. Takie eksperymenty wykonuje się na ćwiczeniach z ekologii (nie zawsze) na bezkręgowcach nie objętych ochroną. Problem w tym, że bezkręgowce jednorazowo składają wiele jaj i w efekcie jeden rozród nie równa się narodzinom jednego potomka – a założenie to było używane we wzorach i omawianych procesach stochastycznych.
Zagęszczeniozależność zupełnie nie pasuje do populacji osobników osiadłych. Tu pojedynczy osobnik nie korzysta z tej samej puli zasobów, z jakich korzysta cała populacja. Założenie, że prawdopodobieństwa rozrodu i śmierci zależą od liczebności populacji, nie mają w tym wypadku sensu. Należałoby raczej rozważyć najbliższych sąsiadów każdego osobnika.
Dlaczego zatem modele zagęszczeniozależne tak bardzo zdominowały ekologię? Bo jest tu dużo fajnej matematyki i matematycy lubią się nimi bawić.
W rozdziałach od 1-5 pewien schemat modelowania populacji obejmujący różne rodzaje modelowania, jakie występują w ekologii teoretycznej.
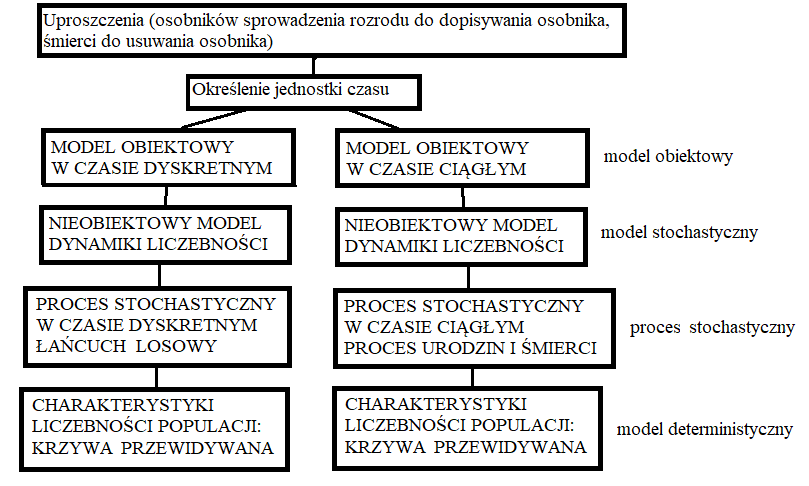 Uproszczenia, nawet skrajne, dotyczą modelu obiektowego populacji. Potem jest już ścisła analiza matematyczna modelu, bez dodatkowych uproszczeń. W ten sposób związki między modelami deterministycznymi i stochastycznymi są bardzo ścisłe. Dla tego samego zestawu parametrów symulacje programów obiektowych i realizacje procesów stochastycznych są takie same i wahają się wokół krzywych tworzonych przez modele deterministyczne. Ponadto symulowany czas w jakim wyliczamy przewidywaną dynamikę liczebności, jest wyrażany w takich samych jednostkach czasu, w jakich wyrażane są intensywności prawdopodobieństwa. Jest to dużo więcej niż operowanie np. modelem logistycznym i twierdzenie z uporem, że on się sprawdza bo “populacje dopasowują się do niego” (naprawdę coś takiego słyszałam i to nie raz, i nie od jednego matematyka).
Uproszczenia, nawet skrajne, dotyczą modelu obiektowego populacji. Potem jest już ścisła analiza matematyczna modelu, bez dodatkowych uproszczeń. W ten sposób związki między modelami deterministycznymi i stochastycznymi są bardzo ścisłe. Dla tego samego zestawu parametrów symulacje programów obiektowych i realizacje procesów stochastycznych są takie same i wahają się wokół krzywych tworzonych przez modele deterministyczne. Ponadto symulowany czas w jakim wyliczamy przewidywaną dynamikę liczebności, jest wyrażany w takich samych jednostkach czasu, w jakich wyrażane są intensywności prawdopodobieństwa. Jest to dużo więcej niż operowanie np. modelem logistycznym i twierdzenie z uporem, że on się sprawdza bo “populacje dopasowują się do niego” (naprawdę coś takiego słyszałam i to nie raz, i nie od jednego matematyka).
Na marginesie, model logistyczny powstanie, jako krzywa przewidywana dynamiki liczebności populacji, gdy w równaniu różniczkowym:
wielkość pr(x)-ps(x) przybliżymy prostą y = K – rx. Gdy rozwiniemy jakąś funkcję w szereg Taylora (jest to wielomian zbieżny do tej funkcji, przynajmniej na pewnym całkiem sporym odcinku, zapisywany w kolejności od wyrazu stałego: a0+a1x+a2x2+…) jej początkowy człon liniowy najlepiej wyjaśnia przebieg funkcji w wybranym kawałku (rośnie czy maleje). Tego typu uproszczenie było powszechnie stosowane w modelowaniu, gdy wszelkie obliczenia wykonywano na papierze. W taki sposób model logistyczny wyprowadzony został przez Alfreda J. Lotkę w jego bardzo niegdyś popularnym podręczniku z 1925 roku. Sam model, zakładający rozrodczość i śmiertelność wyrażające się wzorami liniowymi, powstał prawie 100 lat wcześniej opublikowany przez Pierre-François Verhulsta.
Niestety uproszczenia matematycznie nie likwidują wad tego modelu. Jak ktoś znajdzie rzeczywistą populację, której liczebność rośnie zgodnie z modelem logistycznym (pomijając oczywiście fakt niecałkowitych liczebności, niech to będzie duża, nie całkowita zgodność), to proszę o maila z podaniem źródła.
Na koniec uwaga. Komplikowanie modelu obiektowego jest proste, ale zawsze powoduje komplikowanie zarówno odpowiadających mu procesów stochastycznych jak i krzywych przewidywanych. Komplikowanie w drugą stronę, czyli krzywych przewidywanych, może skutkować powstaniem równań, dla których nie istnieje odpowiedni model obiektowy, a tym samym żadna rzeczywista populacja.