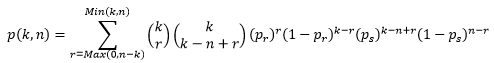Oczekiwane i przewidywane dynamiki liczebności

“Miary” tendencji centralnej

Termin “miara” tendencji centralnej w odniesieniu do liczbowych zbiorów danych jest całkowicie niepoprawny z matematycznego punktu widzenia, gdyż miara ma bardzo ścisłą definicję. Mimo to przyjął się w statystyce i w tych dziedzinach naukowych, gdzie pracuje się z danymi liczbowymi. Oznacza on po prostu takie podstawowe charakterystyki zbioru danych liczbowych jak średnia, mediana i jeszcze kilka innych. Odpowiadają im charakterystyki niekończonych rozkładów takie jak wartość oczekiwana, mediana rozkładu i odpowiednio inne. Średnie i mediany są powszechnie liczone dla danych, a testy statystyczne sprawdzają na ile istotnie zaobserwowane własności dla średnich z prób odnoszą się także do wartości oczekiwanych całych rozkładów. Podobne rozumowania chciałoby się przeprowadzić dla łańcuchów Markowa. Trzeba zatem zdefiniować odpowiedniki “miar centralnych” dla tych procesów stochastycznych.

Łańcuchem Markowa nazywamy ciąg zmiennych losowych indeksowanych liczbami dyskretnymi, które najczęściej utożsamiamy z czasem i nazywamy krokami czasowymi. Zazwyczaj też liczbami indeksującymi zmienne losowe są liczby całkowite nieujemne, chyba, że posługując się rzeczywistymi jednostkami czasu zależy nam bardzo na pokazaniu, kiedy wyliczane są wartości zmiennych. Najczęściej zapisujemy go w postaci:

N₀ → N₁ → N₂ → … → N_tGdy każda ze zmiennych ma wartość oczekiwaną podstawową centralna charakterystyką łańcucha Markowa będzie ciąg wartości oczekiwanych tych zmiennych.

EN₀ → EN₁ → EN₂ → … → EN_tJego przybliżeniem jest ciąg średnich z liczebności w chwili 0,1,…,t uzyskanych po wielu powtórzeniach symulacji programu tworzącego realizacje jakiegoś łańcucha Markowa.

ciąg takich średnich tworzy nam krzywą oczekiwaną charakteryzującą łańcuch Markowa. Istnieje także inna centralna charakterystyka zbioru realizacji procesu stochastycznego mającego własność Markowa – krzywa przewidywana. Jej definicja nie jest tak oczywista jak krzywej oczekiwanej i wytłumaczymy to na przykładzie modelu dynamiki liczebności najprostszej populacji.

Model dynamiki liczebności najprostszej populacji i eksperymentalne wyliczenie krzywej oczekiwanej

Model dynamiki liczebności populacji z zagęszczeniozależnym mechanizmem regulacyjnym obrazuje następujący program:

from random import random
from math import exp
N0=10
ar=-0.005
br=1.0
ass=0.005
bs=0.0
czas=100
lpow=10
tekst='powtorzenie, czas, liczebnosc \n'
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
    N=N0
    ostnr=N0
    t=0
    tekst=tekst+str(pow)+" "+str(t)+" "+str(N)+"\n"
    for t in range(1,czas+1):
        n=0
        pr=1/(1+exp(-(ar*N+br)))
        ps=1/(1+exp(-(ass*N+bs)))
        for i in range(N):
            if random()<pr:
                n=n+1
            if random()<ps:
                pass
            else:
                n=n+1  
        N=n
        if N>100000:
            break
        tekst=tekst+str(pow)+" "+str(t)+" "+str(N)+"\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()

Oczekiwana dynamika liczebności jest funkcją, która każdemu momentowi czasowemu przyporządkowuje wartość oczekiwaną liczebności populacji w tym momencie. Wartości oczekiwane można wyliczać jako średnie liczebności w kroku czasowym t z dynamik liczebności uzyskiwanych po bardzo wielu powtórzeniach symulacji. Tak jak to zrobiono w poniższym programie.

from random import random
from math import exp
N0=10
ar=-0.005
br=1.0
ass=0.005
bs=0.0
czas=100
lpow=1000
tekst=''
wyniki = open('wyniki.txt', 'w')
srdynamika=[]
for t in range(czas+1):
    srdynamika=srdynamika+[[t,0]]

for pow in range(1,lpow+1):
    populacja=[]
    N=N0
    ostnr=N0
    t=0
    srdynamika[0][1]=srdynamika[0][1]+N0
    for t in range(1,czas+1):
        n=0
        pr=1/(1+exp(-(ar*N+br)))
        ps=1/(1+exp(-(ass*N+bs)))
        for i in range(N):
            if random()<pr:
                n=n+1
            if random()<ps:
                pass
            else:
                n=n+1
        N=n
        if N>100000:
            break
        srdynamika[t][1]=srdynamika[t][1]+N
for t in range(czas+1):
    srdynamika[t][1]=srdynamika[t][1]/lpow
    tekst=tekst+str(srdynamika[t][0])+', '+str(srdynamika[t][1])+"\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()

Uruchomienie tego programu pokazuje, że takie średnie dynamiki wyliczają się dość długo. Zależy to oczywiście od liczby powtórzeń symulacji, ale przy małej liczbie powtórzeń średnia liczebność będzie już wyraźnie odbiegać od wartości oczekiwanej. O wiele większy problem stanowi fakt, że wyliczanie średnich dynamik liczebności metodą eksperymentalną zachodzi tylko wtedy, gdy za parametry ar, br, as i bs zostaną wstawione konkretne liczby. Zatem by zorientowanie się, jak każdy z tych parametrów wpływa na dynamikę liczebności, trzeba wykonać wiele eksperymentów. A i tak wyniki interpretowalne byłyby tylko dla jakiegoś ograniczonego zakresu liczb.

Macierz stochastyczna i oczekiwane liczebności populacji

Każdemu łańcuchowi Markowa odpowiada macierz stochastyczna. Jej wyrazami są prawdopodobieństwa przejścia z określonego stanu w chwili t (np liczebności N_t=k) do określonego stanu w chwili t+1 (np. liczebności N_t+1=n). W przypadku łańcuchów jednorodnych (a takim jest dynamika liczebności najprostszej populacji). Taka macierz jest jednakowa dla wszystkich kroków czasowych [0,1), [1,2),…,[t, t+1). Jej wartości można wyliczyć ze wzoru:

Nieznane mi są biblioteki statystyczne Pythona, aby utworzyć program wyliczający w miarę szybko dużą macierz stochastyczną dla parametrów założonych w powyższych programach. W każdym razie po wyliczeniu jej w R uzyskujemy macierz, której początek wygląda następująco:

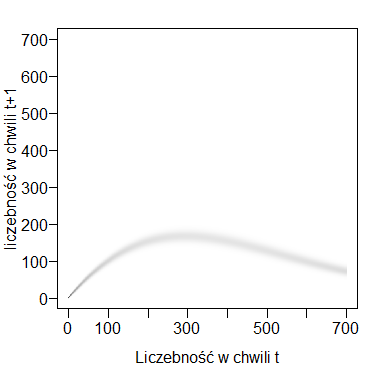
Macierz tę wyliczono dla 701 kolumn i 701 wierszy. Aby ją całą ocenić każde prawdopodobieństwo zobrazowano kropką, której kolor zależał od wartości tego prawdopodobieństwa. Im jest ciemniejszy w skali szarości tym prawdopodobieństwo jest większe. Odpowiedni wykres wygląda następująco:

Posiadając taką macierz bardzo łatwo jest wyliczyć wartości oczekiwane przy założeniu że liczebność w chwili t była równa k. Jest to:

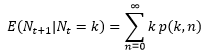Gdzie p(k,n) są prawdopodobieństwami wyliczonymi za pomocą podanego wcześniej wzoru i umieszczonymi w tabeli stochastycznej w k-tej kolumnie. Pozwala to na szybkie wyliczenie EN₁, gdy wiemy, że N0=20. Jest ono równe 23.71941. Niestety wszystko psuje się już w drugim kroku czasowym, bo najpierw należy wyliczyć prawdopodobieństwo całkowite dla wszystkich K, że liczebność populacji w chwili t=2 wyniesie N₂=K pod warunkiem, że w chwili t=1 populacja liczyła N₁ osobników. Daje to już to podwójna sumę na prawdopodobieństwo. Potem można wyliczyć wartość oczekiwaną zmiennej N₂, która będzie wyrażać się sumą iloczynów pewnych wyrażeń. Dla kolejnych kroków czasowych wzór jeszcze bardziej się komplikuje.

Ale z twierdzenia Chapmana-Kołmogorowa wynika, że iloczyn macierzy stochastycznych pokazuje prawdopodobieństwa przejścia ze stanu k w chwili t do stanu n w chwili t+2. Trzecia potęga macierzy stochastycznych pokazuje prawdopodobieństwa przejścia ze stanu k w chwili t do stanu n w chwili t+3. A w t-tej potędze macierzy stochastycznej są prawdopodobieństwa przejścia od chwili 0 do chwili t. To pozwala na wyliczenie wartości oczekiwanych liczebności populacji o ile założona zostanie liczebność początkowa N0=k. Wszystkie obliczenia dotyczyć będą k-tej kolumny tylko kolejnych potęg macierzy stochastycznej. Dla N0=20 kolejne wartości oczekiwane wynoszą:

EN₀=20 → EN₁=23.71941 → EN₂=27.90862 → EN₃=32.54364 → EN₄=37.57011 → EN₅=42.90209 → EN₆=48.42557 → EN₇=54.00694 → EN₈=59.50545 → EN₉=64.78716 → EN₁₀=69.73751 → … →EN₁₀₀= 98.84255 → EN₁₀₁=98.84255.Wszystkie te obliczenia zostały wykonane w R, gdyż wyjątkowo dobrze radzi on sobie z mnożeniem wielkich macierzy kwadratowych. Należałoby poszukać w Pythonie odpowiedniej biblioteki, by równie łatwo radziła sobie z tym problemem, gdy chcemy podobne obliczenia wykonywać w tym programie.

Macierz stochastyczna i przewidywane liczebności populacji

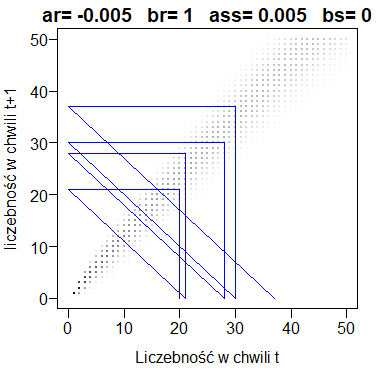
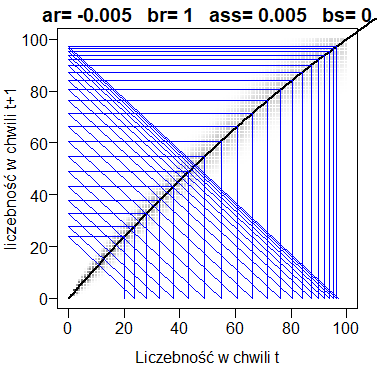
Macierz stochastyczna wsadzona do układu współrzędnych i pokazana jako wykres kropek o różnych odcieniach szarości służy przede wszystkim do przewidywania przebiegu realizacji procesu stochastycznego. Jak się to robi? Ponieważ całkiem białych polach prawdopodobieństwa są praktycznie równe 0 można założyć, że startując od N0=20 i wykonując losowe ustalanie liczebności w chwili następnej trafimy na zaciemniony mniej lub bardziej punkt w kolumnie 20-tej. Odczytamy jakiej to odpowiada liczebności na osi pionowej, a następnie zaznaczamy tę samą liczebność na osi poziomej. Potem operację powtarzamy. Wygląda to tak jak na pokazanym wykresie początkowego fragmentu macierzy stochastycznej.

Widać, że najbardziej prawdopodobne realizacje będą początkowo rosły. Najciekawszy jest fragment macierzy stochastycznej wokół przecięcia 100-tnej kolumny i 100-nego wiersza. Gdy liczebność osiągnie 100 z jednakowym prawdopodobieństwem może być większa lub mniejsza. Gdy spadnie do 50 to kolejna liczebność będzie już raczej większa. Gdy liczebność wzrośnie do 140, to kolejna liczebność będzie najczęściej mniejsza. Widać to dobrze gdy na wykresie zostanie dorysowana przekątna, czyli prosta y=x.

Innymi słowy przewidujemy, że populacja będzie się wahała wokół 100 z najczęstszą amplitudą znacznie mniejszą od 90.

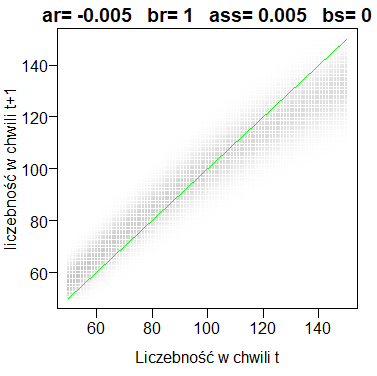
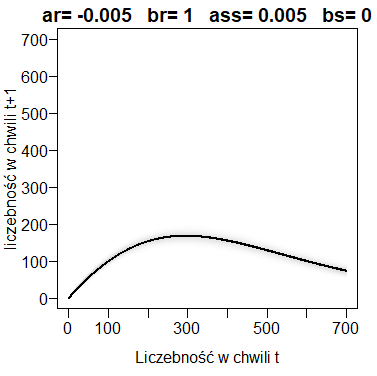
Na wykresie macierzy stochastycznej możemy zaznaczyć warunkowe wartości oczekiwane. Są one możliwe do wyliczenia, nawet gdy operujemy tylko wzorem na prawdopodobieństwa. Załóżmy, że w chwili t populacja liczy k osobników. Wartość oczekiwana osobników, które rozrodzą się w czasie [t,t+1) jest równa k*pr(k). Wartość oczekiwana osobników, które umrą w czasie [t,t+1) jest równa k*pr(k). Są to bowiem wartości oczekiwane rozkładu dwumianowego, z którego losowane są liczby osobników rozradzających się i zmarłych. Zatem wartość oczekiwana liczby osobników w chwili t+1 pod warunkiem, że w chwili t była równa k wynosi:

E(N_t+1|N_t=k)=k+k*pr(k)-k*ps(k)Zaznaczmy te wartości na macierzy stochastycznej.

Jak można się było spodziewać, przechodzi ona dokładnie przez środek najbardziej zaciemnionego obszaru wykresu. Krzywa przewidywana to taka krzywa, Która powstaje przez wędrowanie od wartości początkowej tak, jak to pokazano w poprzednich przykładach, ale której kolejne wartości zawsze leżą na pokazanej funkcji łączącej warunkowe wartości oczekiwane, przy czym mówimy tu o wykresie funkcji rzeczywistej f(x)=x+x*pr(x)-x*ps(x).

Mówiąc inaczej, krzywa przewidywana to ciąg rekurencyjny x_n zdefiniowany następująco:

x₀ = N₀x_t+1 = xt + xt*pr(x) – xt*ps(x)

Wyliczanie takiego ciągu jest dużo prostsze od wyliczenia krzywej oczekiwanej. A jest to ciąg mający dla większości parametrów wartości bardzo bliskie wartościom oczekiwanym liczebności w kolejnych krokach czasowych. Dla parametrów i funkcji logistycznych rozważanych w programach kolejne wartości tego ciągu wynoszą:

PredN₀=20 → PredN₁=23.71941 → PredN₂=27.92956 → PredN₃=32.61835 → predN₄=37.74369 → PredN₅=43.22945 → PredN₆=48.96524 → PredN₇=54.81181 → PredN₈=60.61226 → PredN₉=66.20786 → PredN₁₀=71.45537 → … →PredN₁₀₀= 100 → PredN₁₀₁=100Różnice między krzywą przewidywaną a oczekiwaną są nieznaczne. Od razu dodam, że nie jest to regułą dla wszystkich parametrów ar, br, as i bs.

Zastosowanie krzywej oczekiwanej i przewidywanej

Tak jak wartość oczekiwana rozkładu jest najważniejszą jego charakterystyką centralną, tak krzywa oczekiwana jest najważniejsza charakterystyką łańcucha Markowa. Ale krzywa przewidywana ma większe zastosowanie praktyczne, głównie ze względu na łatwość jej wyliczania w różnych programach i to, że wyraża się wzorem, w którym występują parametry programu.

Realizacje wielu łańcuchów Markowa wahają się w mniej lub bardziej nieregularny sposób. Wyliczenie krzywej przewidywanej przed rozpoczęciem symulacji pozwala przewidzieć wokół jakiej liczby będą się one wahały.

Krzywe przewidywane pozwalają na dobranie parametrów No, ar, br, as i bs aby symulowana populacja nie była zbyt duża ani zaraz nie wymarła. I robi się to bez zbędnych symulacji próbnych. Pozwalają one na ustalanie skali wykresów, w których obrazowane są symulacje w czasie rzeczywistym, zwłaszcza gdy programy te dopuszczają zmianę parametrów programu.

Analiza wpływu parametrów na przebieg dynamik liczebności wymagałaby wielu powtórzeń symulacji. A tymczasem bardzo często wystarczy zbadać wpływ wartości parametrów na przebieg krzywych przewidywanych by skutecznie przewidzieć, co wygeneruje symulator łańcuchów Markowa. Będzie to przedmiotem zadania dla studentów.

Krzywe przewidywane, tak jak wszystkie ciągi rekurencyjne, pozwalają na mówienie o ich stabilności i niestabilności (kiedy mają stany równowagi). Ale o tej najważniejszej własności krzywych przewidywanych będą mówić inne osoby.

Zadanie dla studentów

Na początek dla przykładowych parametrów należy wyliczyć dziesięć przykładowych dynamik, oczekiwaną dynamikę liczebności dla 1000 powtórzeń symulacji i przewidywaną dynamikę. Tę ostatnią wystarczy wyliczyć w arkuszu kalkulacyjnym, do którego trzeba przenieść wyniki z obu programów (uwaga – ta sama nazwa zbioru wynikowego).

Sposób wyliczenia przewidywanej dynamiki liczebności:

• Otworzyć Excela lub arkusz kalkulacyjny
• W polu A1 napisać ar, a w polu B1 jego wartość
• W polu A2 napisać br, a w polu B2 jego wartość
• W polu A3 napisać as, a w polu B3 jego wartość
• W polu A4 napisać bs, a w polu B4 jego wartość
• W polu A5 napisać , a w polu B5 jej wartość
• W polu C1 napisać czas
• W polu C2 napisać 0, w C3 napisać 1 i przeciągnąć oba pola do C102 (przeciągnąć oznacza chwycić zaznaczone pola za prawy dolny róg, gdy kursor zamienia się w krzyżyk). Powinny tam pojawić się kolejne liczby od 0 do 100.
• W polu D1 napisać pr. Pole D2 zostawić puste
• W polu D3 napisać =1/(1+exp(-($B$1*F2+$B$2)))
• W polu E1 napisać ps. Pole E2 zostawić puste
• W polu E3 napisać =1/(1+exp(-($B$3*F2+$B$4)))
• W polu F1 napisać N
• W polu F2 napisać =$B$5
• W polu F3 napisać =F2+D3*F2-E3*F2
• Zaznaczyć pola D3-F3
• Przeciągnąć do wiersza 102
• Zaznaczyć pola C1:C102 i F1:F102 (zaznaczanie rozłącznych obszarów w Excelu wykonać można trzymając Ctrl po zaznaczeniu pierwszego kawałka)
• Kliknąć na ikonkę “kreator wykresów”
• Wybrać typ wykresu – punktowy
• Wybrać podtyp – liniowy
• Podpisać osie. Zatytułować wykres.

Plik należy zapamiętać. Następnie wykonujemy 10 powtórzeń symulacji (pierwszy program). Wprowadzamy wyniki do wykonanego wcześniej pliku i układamy liczebności z 10 powtórzeń obok siebie. Dodajemy do wykonanego wykresu te dynamiki. Czy wahają się one wokół wartości przewidywanych? Jeżeli nie, gdzieś został zrobiony błąd i trzeba albo poprawić wyliczenia w Excelu albo symulację powtórzyć. Po wyeliminowaniu błędów zapamiętać.

Wykonać drugi program i wyniki wprowadzić do zrobionego pliku. Oczekiwaną dynamikę liczebności dodać do zrobionego wykresu. Czy pokrywa się ona z dynamiką przewidywaną?

Wykonane czynności powtórzyć dla parametrów: ar=-0.001, br=1, as=0.001, bs=0 i wykonać nowy wykres.

Wykonane czynności powtórzyć dla parametrów: ar=-0.0005, br=5, as=0.0005, bs=-5 i wykonać nowy wykres.

Zmieniać wartości parametrów ar, br, as i bs w pliku , w którym narysowana jest tylko przewidywana dynamika liczebności populacji. Dodatkowo obok zrobić wykresy funkcji pr(N) i ps(N).

• W polu H1 napisać liczebność
• W polu H2 napisać 0, w H3 napisać 1 i przeciągnąć oba pola do C502 (przeciągnąć oznacza chwycić zaznaczone pola za prawy dolny róg, gdy kursor zamienia się w krzyżyk). Powinny tam pojawić się kolejne liczby od 0 do 500.
• W polu I1 napisać pr.
• W polu I2 napisać =1/(1+exp(-($B$1*H2+$B$2)))
• W polu J1 napisać ps.
• W polu J2 napisać =1/(1+exp(-($B$3*F2+$B$4)))
• Zaznaczyć pola I2-J2
• Przeciągnąć do wiersza 502
• Zaznaczyć pola H1:J502
• Kliknąć na ikonkę “kreator wykresów”
• Wybrać typ wykresu – punktowy
• Wybrać podtyp – liniowy
• Podpisać osie. Zatytułować wykres.

Co powoduje przybliżanie do zera liczb ar i as? Co powoduje zwiększanie odstępu między br i bs? Czy istnieją parametry, które oznaczają tak dużymi wahaniami dynamik liczebności, że prawdopodobieństwo wymarcia populacji jest duże? Sprawdzić robiąc dla takich parametrów symulacje.

Odpowiedzieć na pytanie – czy warto liczyć przewidywane dynamiki liczebności? Należy uwzględnić zarówno interes modelarzy chcących zrobić ładny model komputerowy populacji oraz interes ekologów pracujących z prawdziwymi populacjami.