Stabilność, niestabilność i chaos
Definicje obiegowo rozumianej stabilności i chaosu
Słowo “stabilność” używane jest powszechnie w wielu dziedzinach nauki i generalnie ludzie wiedzą o nim tyle, że dobrze by jakiś układ, system, maszyna itp. były stabilne. Słowo to używane jest w odniesieniu do partii politycznych, pacjentów szpitali, maszyn, automatów, programów komputerowych, klimatu a także populacji i ekosystemów. Ze stabilnością wiąże się długi czas działania obiektów lub systemów określanych jako stabilne, ale nie jest to synonim trwałości. Co to zatem znaczy stabilność? Co to znaczy niestabilność?
| Encyklopedia PWN |
| Stabilność [łac.] (mech., autom.) jedna z podstawowych właściwości układów dynamicznych, polegająca na tym, że układ samoistnie powraca w dowolnie dobrane otoczenie swojego stanu równowagi lub w dowolnie dobrane otoczenie ustalonych warunków pracy układu (np. drgań ustalonych), z którego, lub których, został wytrącony odpowiednio małym (w stosunku do przyjętego bliskiego otoczenia) i przemijającym zaburzeniem. stabilność (mat.) termin występujący w różnorodnych znaczeniach w wielu dziedzinach matematyki, m.in. w równaniach różniczkowych, układach dynamicznych, procesach stochastycznych, teorii gier. |
Generalnie zatem stabilność oznacza:
- Istnienie stanu równowagi.
- Powracanie do stanu równowagi po większych lub mniejszych zaburzeniach.
Równie dużo znaczeń ma słowo chaos. Słowo pochodzi ze starożytnej Grecji i oznaczało stan w jakim znajdował się świat zanim powstała Ziemia i bogowie. Czy oznacza to bałagan, zamieszanie, losowość w rozmieszczeniu obiektów czy coś innego?
| Encyklopedia PWN |
| Chaos [gr., rozziew, pustka, bezkształt] (filoz.) pojęcie wywodzące się ze starożytnej greckiej mitologii i filozofii, synonim bezładu, nieokreśloności. Chaos [gr., rozziew, pustka, bezkształt], mit. gr. uosobienie stanu istniejącego przed powstaniem świata. chaos deterministyczny (fiz.) nieregularne, nieuporządkowane zachowanie się układów deterministycznych, praktycznie nieprzewidywalne w dłuższych przedziałach czasu. |
Chaos kojarzy się z totalnym bałaganem i całkowicie nieprzewidywalnymi stanami układu. Nie oznacza to jednak, że nie istnieją w nim stany równowagi. Mogą istnieć, a nawet może ich być nieskończenie wiele, tyle tylko, że nie obserwujemy powrotów do stanu równowagi, bądź nie potrafimy przewidzieć do którego stanu równowagi zmierzać będzie układ.
Matematyczne definicje stabilności i chaosu
Pojęcia stabilności i chaosu występują w różnych dziedzinach matematyki, jednak ich ścisła definicja dotyczy teorii równań różniczkowych i różnicowych (wyrażanych ciągani rekurencyjnymi. Równania typu:
![]() dla funkcji x(t) ciągłej i różniczkowalnej, oraz:
dla funkcji x(t) ciągłej i różniczkowalnej, oraz:
dla wielkości xt zależących od czasu w sposób dyskretny (czyli będących ciągami rekurencyjnymi), rozwiązania zależą od wartości początkowych ustalanych zwyczajowo w chwili t=0. To chwile zaburzeń układu.
| Henryk Żołądek. Jakościowa teoria równań różniczkowych zwyczajnych. Uniwersytet Warszawski 2011. |
| Dla równania różniczkowego dx/dt=F(x,t) punkt x* taki, że
F(x*,t)=0 (dla każdego t) nazywa się stanem równowagi. |
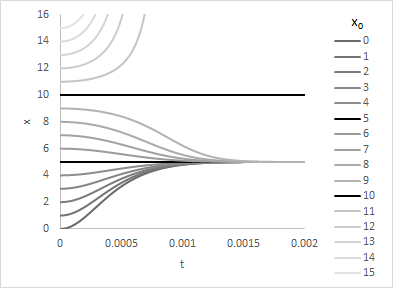
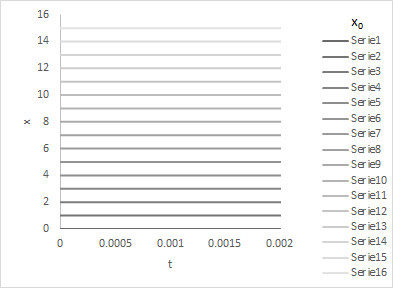
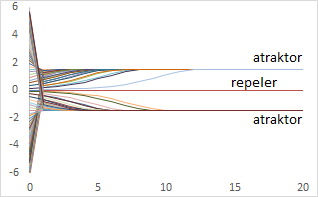
Definicja ta dotyczy także równania rekurencyjnego, zwanego także równaniem różnicowym. Niestety nie jest ona wystarczająca dla biologów, którzy ze względu na rytmy sezonowe a także dobowe wielu zjawisk w przyrodzie za stan równowagi uznaliby pewną krzywą ograniczoną. Byłoby to takie rozwiązanie układu różniczkowego lub różnicowego, które pozostaje po nieskończenie długim czasie. Nie byłoby ono określone jednoznacznie, jako że po nieskończenie długim czasie nie wiadomo kiedy funkcja się zaczyna, ale po odpowiednich przesunięciach w lewo lub prawo funkcje te nałożyłyby się na siebie. Różne stany równowagi (zaznaczone na czarno) wśród innych rozwiązań obrazują poniższe wykresy:
Zachowanie się rozwiązań równań różniczkowych i różnicowych względem stanów równowagi wyróżnia wśród nich stany stabilne (atraktory – przyciągające rozwiązania) i niestabilne (repelery – odstraszacze). Niestety obserwuje się jeszcze inne zjawiska. Stabilność definiuje się na kilka sposobów wśród których najważniejsze to:
| Henryk Żołądek. Jakościowa teoria równań różniczkowych zwyczajnych. Uniwersytet Warszawski 2011. |
| Stan równowagi x* jest stabilny w sensie Lapunowa, jeżeli dla każdego ε>0 istnieją δ>0 oraz czas t* takie, że każde rozwiązanie x=φ(t) startujące z otoczenia (x*-δ,x*+δ) pozostaje w obszarze (x*-ε,x*+ε) dla każdego t>t*.
Stan równowagi x* jest stabilny asymptotycznie, jeżeli istnieje δ>0 taki, że każde rozwiązanie x=φ(t) startujące z otoczenia (x*-δ,x*+δ) dąży do x* przy t →∞. |
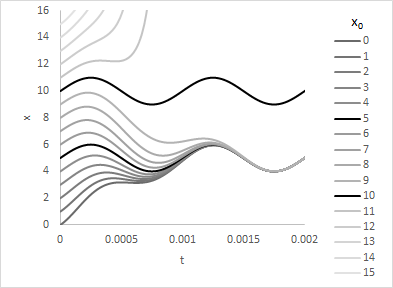
Różnicę między nimi obrazują następujące wykresy obrazujące rozwiązania równania różniczkowego (różnicowego) złożonego z samych stanów równowago. Są one stabilne w sensie Lapunowa i niestabilne asymptotycznie.
Niestabilność to brak stabilności. Ale mogą się za tym kryć różne zjawiska
- Brak stanu równowagi.
- Istnienie stanu równowagi x*, ale każdym jego otwartym otoczeniu istnieje taki punkt początkowy, że wyprowadzone z niego rozwiązanie nie zmierza do x*.
- Punkty, z których rozwiązania nie zmierzają do x*, tworzą zbiór dyskretny w (x*-δ,x*+δ) i prawdopodobieństwo ich wylosowania jest równe 0.
- Punty, z których rozwiązania zmierzają do x*, tworzą zbiór dyskretny w (x*-δ,x*+δ) i prawdopodobieństwo ich wylosowania jest równe 0.
- Istnienie stanu równowagi x*, ale wszystkie rozwiązania wyprowadzone z jego otwartego otoczenia oddalają się of niego.
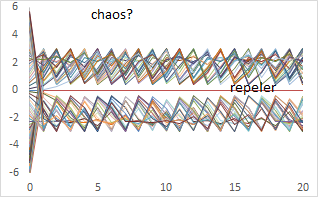
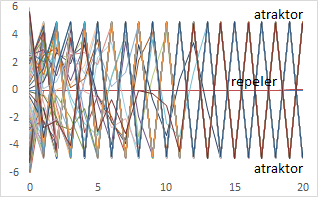
O ile punkt 1 i 3 pokazują oczywistą niestabilność, o tyle punkt 2 z podpunktem pierwszym traktowany jest czasem jak stabilność, a z podpunktem drugim jak niestabilność. W obrębie punktu 2.2 pojawić się mogą układy zwane chaosem.
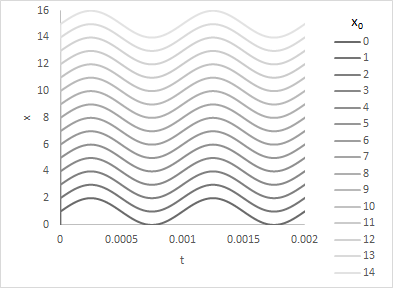
Chaos deterministyczny nie ma ścisłej matematycznej definicji. Jest to własność równań lub układów równań różniczkowych lub różnicowych polegająca na dużej wrażliwości rozwiązań na dowolnie małe zaburzenie parametrów. Rozwiązania wyprowadzone z dowolnie bliskich punktów początkowych będą się różnić się od siebie siebie przynajmniej w niektórych momentach czasowych. O chaosie mówimy najczęściej wtedy, gdy układ ma nieskończenie wiele stanów równowagi wzajemnie się przeplatających ze sobą i pozostałe równania zmierzają do któregoś z nich nie tworząc przy tym grup rozwiązań wychodzących z jakiegoś zbioru otwartego. Trudności w rozróżnieniu stabilności, niestabilności i chaosu pokazują następujące wykresy:
Powstają one dla równań różnicowych, gdyż dla równań różnicowych obowiązuje prawo Cauchy’ego – ich rozwiązania nie mogą się przecinać. Dla równań różnicowych rozwiązania, jako ciągi, mogą się mijać , choć gdy przyjmą w jakimś czasie jednakowa wartość to w dalszych momentach czasowych będą już sobie równe. Na wykresach ich wartości połączono kreskami, stąd pozorne punkty wspólne.
Stabilność, a modele populacji
Najbardziej znanymi modelami populacji są:
- model wykładniczy: liczebność populacji spełnia równanie różniczkowe dN/dt = cN dla c>0
- model logistyczny: liczebność populacji spełnia równanie różniczkowe dN/dt = N(aN+b) dla a<0 i b>0
- model logistyczny populacji w czasie dyskretnym: liczebność populacji spełnia równanie różnicowe Nt+1=Nt + Nt(aNt+b)
Są to tak naprawdę charakterystyki statystyczne (zbiorcze) liczebności populacji, które można uzyskać w modelach obiektowych najprostszej populacji (opisano je jako krzywe przewidywane). Jako charakterystyki statystyczne mogą przyjmować wartości niecałkowite, tak samo jak średnia z liczb całkowitych nie musi być liczbą całkowitą.
Należy przeprowadzić analizę ich stabilności/nie stabilności. O ile z modelami różniczkowymi łatwo sobie poradzić o tyle model logistyczny w czasie dyskretnym może zaskoczyć. Na szczęście w Excelu bardzo łatwo jest wykonać taki model z możliwością podmiany parametrów i błyskawicznymi zmianami obserwowanymi na wykresach.
- Excelu lub arkuszu kalkulacyjnym w polu A1:A4 wpisać nazwy parametrów (ar,br,as,bs) stosowanych w funkcjach pr(N)=arN+br i ps(N)=asN+bs, a w polach B1:B4 wartości tych parametrów (na początek -0.005, 1, 0.005, 0).
- W polu C1 napisać czas, w polu C2 wpisać 0, w polu C3 wpisać 1. Zaznaczyć pola C2:C3 i przeciągnąć je w dół do pola C102.
- W polu D1,E1,F1,… wpisać liczebności początkowe (mp 20, 40, ……, 200)
- W pola D2,E2,F2,…wpisać na początek 10, 20, 30, ….
- W polu D3 wpisać formułę: =D2+D2*($B$1*D2+$B$2)-D2*($B$3*D2+$B$4)
- Chwycić za prawy dolny róg i przeciągnąć przez kolejne kolumny. Potem przeciągnąć cały zaznaczony wiersz w dół do wiersza 103
- Wykonać wykres zależności liczebności od czasu dla różnych liczebności początkowych
- Można teraz zmieniać wartości ar, br i as i bs aby uzyskać wykresy najbardziej ciekawe. Nie można za bardzo z tym szaleć, bo łatwo uzyskać można wartości spoza skali właściwej dla liczb podwójnej precyzji. Pewną podpowiedzią mogą być pokazane wykresy:
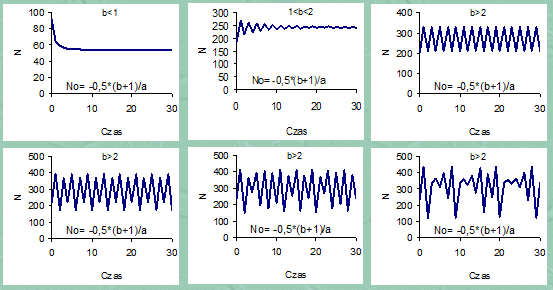
gdzie a=ar-as oraz b=br-bs. Liczba a musi być ujemna i najlepiej dość bliska zeru. Liczba b musi być dodatnia i mniejsza od 3, choć b=3 nie od razu pokaże błędne wartości. Liczebność początkowa nie może przekroczyć -(b+1)/a.
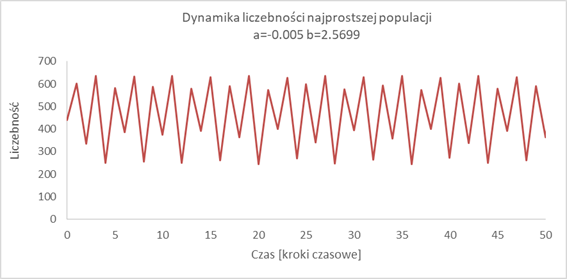
Gdy b=br-bs=2 dynamika bardzo wolno, ale konsekwentnie zmierza do stanu równowagi równego -b/a. Gdy b=br-bs>2 dynamiki wykazują trwałe wahania, ale na początku zmierzają do dwóch stanów równowagi (stan Nt=-b/a staje się repelerem), potem do czterech, ośmiu, szesnastu. Zmiany wartości b przy komplikowaniu się wykresu są coraz mniejsze i dla b=2.5699… (liczba niewymierna) jest ich nieskończenie wiele (aczkolwiek przeliczalnie wiele), rozwiązania z różnych punktów zmierzają do jednego z tych stanów równowagi, ale w każdym otoczeniu takiego stanu równowagi znajduje się nieskończenie wiele punktów, z których wyprowadzone rozwiązania zmierzają do innych stanów równowagi. Mamy układ zwany chaosem. Ale wygląda on mało chaotycznie. Pojedyncze rozwiązanie wydaje się być dość przewidywalne, co do dalszego przebiegu dynamiki:
Dopiero nałożenie na ten wykres rozwiązań wyprowadzonych z innych punktów pokazuje, że wykresy te (czubki wahań) nie pokrywają się, choć różnice między punktami (czubkami wahań dynamiki) nie są zbyt duże. Istnienie nieskończenie wielu stanów równowago nie wskazuje, że te stany równowagi bardzo różnią się od siebie. Tak samo nieskończona liczba punktów w odcinku nie pokazuje, że jest on długi.
Innymi słowy mamy tu nieduży chaos. Chaos związany z istnieniem nieskończenie wielu stanów równowagi powinno się mierzyć za pomocą miary analogicznie zdefiniowanej do długości. Może komuś to się uda zdefiniować.
Stabilność a trwałość układu
Często można przeczytać, że stabilność jakiegoś układu jest gwarancją jego trwałości. Ale dowodu matematycznego na to nie ma. Na przykładzie modelu obiektowego najprostszej populacji można sprawdzić zależność między stabilnością, a trwałością populacji. Model obiektowy dynamiki liczebności najprostszej populacji generuje dynamiki takie same jak model urodzin i śmierci w czasie dyskretnym. Przy pewnych parametrach populacja dość szybko wymiera, przy innych nie. W Pythonie można szybko uzyskiwać takie dynamiki za pomocą programu:
from random import random
N0=100
ar=-0.005
br=1
ass=0.005
bs=0
czas=100
lpow=10
tekst=''
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
N=N0
ostnr=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
for t in range(1,czas+1):
n=0
pr=ar*N+br
ps=ass*N+bs
if (pr<0 or pr>1):
break
if (ps<0 or pr>1):
break
for i in range(N):
if random()<pr:
n=n+1
if random()<ps:
pass
else:
n=n+1
N=n
if N>100000:
break
tekst = tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Jednocześnie charakterystyką statystyczną generowanych dynamik jest ciąg
X0=X0
Xt+1=Xt + Xt*((ar-as)*Xt+(br-bs)).
wyliczony dla tych samych ar,br,as i bs jak w programie.
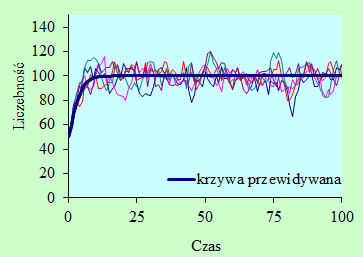
Związek między uzyskanymi wynikami, a krzywą przewidywaną można zobrazować następującymi wykresami:
Dynamiki przewidywane mają identyczny wzór, jak logistyczny modelem populacji w czasie dyskretnym. Charakteryzują się stabilnością, niestabilnością lub chaosem. Można zatem mówić o stabilnych i niestabilnych populacjach, jeżeli ich krzywe przewidywane są stabilne, niestabilne, cechują się chaosem. Sprawdzić jak tak charakteryzowany przebieg krzywych przewidywanych wpływa na przebieg samych dynamik liczebności.
Zadanie dla studentów
- Wybrać kilka (minimum 3) zestawów parametrów ar,br,as i bs które dają różniące się od siebie wykresy przewidywanej dynamiki liczebności pod względem oceny stabilności. Zastosować przy tym pewne założenia, które zapobiegną szybkiemu osiąganiu przez populacje takich liczebności, że prawdopodobieństwa pr=ar*N+br lub ps=ass*N+bs wyjdą poza przedział [0.1]. Na przykład będą przecinać się w środku przedziału [0.1] dla N=100. Można przy ty założyć, że as=-ar.
- Wyliczyć w rkuszu kalkulacyjnym przewidywaną dynamiki liczebności dla założonych ar, br, ass, bs. Można wzorować się na następującym widoku arkusza, w którym wystarczy przeciagnać w dół wpisany wzór by uzyskać przewidywana dynamikę.
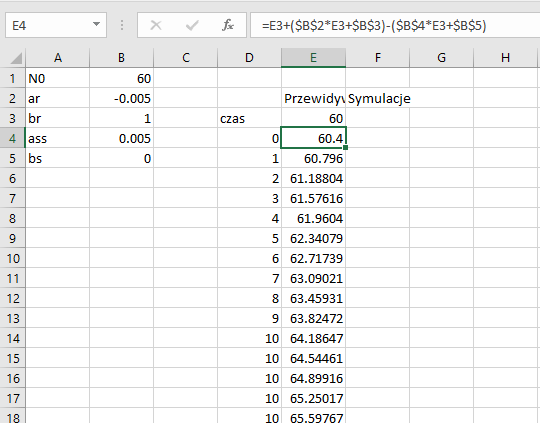
- Wykonać symulację najprostszej populacji dla takich samych parametrów.
- Symulowane dynamiki zapisane w “wyniki.txt” wprowadzić do arkusza kalkulacyjnego. Należy najpierw otworzyć arkusz kalkulacyjny. Wybrać otwórz pliki, zmienić typ pliku na tekstowe i wybrać wyniki.txt. Dopiero wtedy można będzie umieścić dane w osobnych kolumnach (wystarczy odhaczyć separator kolumn jako spację). Skopiować je do przygotowanego wcześniej pliku arkusza do kolejnych kolumn F, G, …
- Wykonać ich wykres jako liniowy bez znaczników.
- Krzywą przewidywaną zaznaczyć jako pierwszą i wyróżnić ja kolorem np. czarnym.
- Wykonać druga symulacją dla ar i as podzielonych przez 10. Taka zmiana nie zmieni kształtu krzywej przewidywanej, a co z symulacją?
- Wykonać ponownie zadanie dla takich samych ar i ass oraz br-bs=2.2 (2 strabilne stany równowagi). Jak wtedy wyglądają symulowane dynamiki liczebności.
- Wykonać ponownie zadanie dla takich samych ar i ass oraz br-bs=2.569947 (chaos). Jak wtedy wyglądają symulowane dynamiki liczebności. Czy układ przestał być trwały? Rozróżnić wymarcie populacji od uzyskania przez nią liczebności, dla której wartości prawdopodobieństw stają się spoza przedziału [0,1].
- Otrzymane wyniki porównać z modelem w którym ar=0, ass=0, br=0.5 i bs=0.5. Liczebność początkową wybrać taka jak stan równowagi w poprzednich modelach.