Zagęszczeniozależne mechanizmy regulacyjne
Geneza zagęszczeniozaleźności
W rzeczywistym środowisku nigdy prawdopodobieństwo śmierci i rozrodu nie jest takie samo. Przy wzroście liczebności populacji na jednego osobnika przypada mniej zasobów. Możemy spodziewać się wzrostu śmiertelności i spadku rozrodczości (albo przynajmniej zmiany prawdopodobieństwa jednego z tych zdarzeń). Schemat rozumowania wygląda tak:
Prawdopodobieństwo rozrodu maleje przy zmniejszaniu się zasobów przypadających na jednego osobnika.
Ilość zasobów przypadających na jednego osobnika maleje przy wzroście liczebności populacji.
⇓
Prawdopodobieństwo rozrodu maleje przy wzroście liczebności populacji.
Prawdopodobieństwo śmierci rośnie przy zmniejszaniu się zasobów przypadających na jednego osobnika.
Ilość zasobów przypadających na jednego osobnika maleje przy wzroście liczebności populacji.
⇓
Prawdopodobieństwo śmierci rośnie przy wzroście liczebności populacji.
Jest to klasyczne założenie modeli zagęszczeniozależnych (tak naprawdę są to modele liczebnościozależne, ale brzmi to okropnie). Modele tego typu dominują w ekologii i tylko niektórzy modelarze rozważają zasoby jako osobną wielkość zastępująca liczebność we wzorze na prawdopodobieństwa, a jednocześnie cechującą się różnie definiowanym odnawianiem. W naszych rozważaniach ograniczymy się do modeli zagęszczeniozależnych.
Matematyczny opis zageszczeniozaleźności
Zakładamy, że prawdopodobieństwa śmierci i rozrodu są funkcjami liczebności populacji. Jaką jednak funkcję wybrać do opisu tego zjawiska?
Typowe dla fizyków podejście kazałoby w pierwszej kolejności analizować funkcje liniowe:
prawdopodobieństwo=a*N+b.Parametr a oznacza wtedy tempo zmian (wzrostu/spadku) prawdopodobieństwa przy wzroście liczebności. Dla prawdopodobieństwa rozrody byłaby to liczba ujemna, dla prawdopodobieństwa śmierci dodatnie. Parametr b oznacza prawdopodobieństwo przy minimalnej liczebności populacji. Matematyk natychmiast zauważy, że funkcje liniowe tylko dla pewnego ograniczonego przedziału liczebności przyjmują wartości z przedziału [0,1], które mogłyby być uznawane za prawdopodobieństwa.
Dla ekologów tego typu rozważania mają wyłącznie “akademicki” charakter. Ważne jest to, jak wyglądają zależności śmiertelności i rozrodczości od liczebności rzeczywistych populacji. Można je wyliczyć eksperymentalnie.
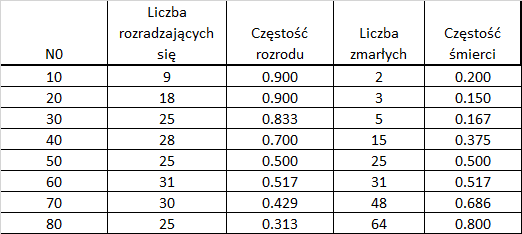
Załóżmy, że badany organizm może (ale nie musi) rozmnażać się tylko raz w okresie Δt i wtedy wydaje na świat jednego potomka. Zakładamy hodowle takich organizmów w akwariach, w których umieszczamy 10, 20, 30, 40, 50, 60, 70 i 80 organizmów populacji początkowej. Organizmy dokarmiamy wsypując do każdego akwarium dokładnie taką samą dawkę pokarmu. Hodowlę prowadzimy przez czas Δt i po tym czasie liczymy ile organizmów populacji początkowej przeżyło i ile podjęło rozród. Wyniki mogą wyglądać następująco:
Częstości śmierci i rozrodu są pewnymi zmiennymi losowymi, ale w dużym stopniu pokrywają się z prawdopodobieństwami tych zdarzeń. Biorąc pod uwagę, że liczba zdarzeń takich jak rozród, czy śmierć ma rozkład dwumianowy można powiedzieć, że częstości rozrodu i śmierci wahają się wokół prawdopodobieństw śmierci i rozrodu osobnika. Prawdopodobieństwa te rosną w miarę wzrostu liczebności populacji i najlepszym ich oszacowaniem byłaby jakaś regresja. Dla regresji liniowych łatwo jest uzyskać określone równania w wielu programach, także w arkuszu kalkulacyjnym.
Dla informatyka modelowanie przy funkcjach liniowych jest problematyczne – wymagałoby ograniczenia zbioru możliwych wartości parametrów służących do wyliczania prawdopodobieństw, a i tak przy stosowaniu losowych procedur nie ma gwarancji, że w pewnym momencie symulacji liczebność populacji stanie się zbyt duża, a wyliczone dla niej prawdopodobieństwa będą albo mniejsze od 0 albo większe od 1. Co wtedy ma zrobić program? By nie generować błędów, należałoby przerwać obliczenia. Nie oznaczałoby to nic znaczącego dla modelowanej populacji ponad to, że weszła ona w inny rodzaj mechanizmów regulacyjnych, których nie uwzględniono w modelu, więc symulacje przerwano. Lepszym sposobem jest zastosowanie regresji nieliniowych, a konkretnie wybieranie regresji z rodziny funkcji, których zbiór wartości zawiera się w przedziale [0,1].
Model najprostszej populacji z zageszczeniozależnym mechanizmem regulacyjnym
Załóżmy, że udało się nam ustalić za pomocą wyliczania regresji nieliniowych jakieś funkcje pr(N) i ps(N), których zbiór wartości przynajmniej dla liczb nieujemnych znajduje się w przedziale [0,1]. Pozwalają one na wyliczanie prawdopodobieństw śmierci i rozrodu w każdym kroku czasowym [t, t+1) na podstawie liczebności w chwili t (zawsze bierze się pod uwagę początek przedziału czasowego, bo to liczebność na początku tego przedziału oznacza jaka będzie dystrybucja zasobów w najbliższej przyszłości). Program symulujący najprostszą populację z zagęszczeniozależnym mechanizmem regulacyjnym wygląda następująco:
from random import random
N0=10
ar=-0.0091
br=1.0446
ass=0.0096
bs=-0.0072
czas=100
lpow=10
tekst=''
wyniki = open('wyniki.txt', 'w')
for pow in range(1,lpow+1):
N=N0
ostnr=N0
t=0
tekst=tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
for t in range(1,czas+1):
n=0
pr=fr(N)
ps=fs(N)
if (pr<0 or pr>1):
break
if (ps<0 or ps>1):
break
for i in range(N):
if random()<pr:
n=n+1
if random()<ps:
pass
else:
n=n+1
N=n
if N>100000:
break
tekst = tekst + str(pow) + ", " + str(t) + ", " + str(N) + "\n"
open('wyniki.txt', 'a').write(tekst)
wyniki.close()
|
Skopiowanie go do IDLE Pythona i próba uruchomienia wygeneruje błędy z powodu braku wzoru dla funkcji fr() i fs(). I tu pojawia się problem nierozstrzygalny metodami eksperymentalnymi: jaką rodzinę funkcji wybrać do wyliczania regresji nieliniowych? Po pierwsze ograniczymy się do rodzin funkcji monotonicznych. Po drugie zastosujemy minimalną liczbę parametrów, a więc rodzin funkcji dwuargumentowych. Przykłady takich funkcji to:
Wykresy pokazane na rysunku zostały wygenerowane dla wielomianu w(N) = 0.005*N-3. Można w to miejsce wstawić dowolny wielomian, a cała funkcja będzie miała wartości w przedziale [0,1]. Funkcja exp( ) – to e( ). Funkcję arcus tangens (odwrotną do tangens) zapisuje się w Pythonie jako atan( ). Obie funkcje exp() i atan() należą do biblioteki math. Funkcja z podwójnym exp(-exp()) nosi nazwę funkcji Gompertza. Nie są to jedyne funkcje przyjmujące wartości w przedziale [0,1]. Jest ich wiele. Pomimo, że wyrażają się skomplikowanym wzorem, ich wyliczanie za pomocą komputera jest proste (wystarczy wpisać wzory i nazwy prawidłowo interpretowane przez Pythona lub inny program).
Metody wyliczania regresji nieliniowych
Poza wyborem rodziny funkcji mających wartości w przedziale [0,1] istnieje także problem metody szacowania parametrów regresji, czyli funkcji najlepiej dopasowanej do danych.
Regresja i linia trendu, najczęściej wybierane są z danej rodziny funkcji w oparciu o kryterium zwane metodą najmniejszych kwadratów. Oznacza to, że wielkości ∑(yi-pr(xi))2 (gdzie yi oznacza częstość rozrodu przy liczebności xi) oraz ∑(yi-ps(xi))2 (gdzie yi oznacza częstość śmierci przy liczebności xi) osiągają minimum. Dla wielu rodzin funkcji takie kryterium nie pozwala na wyprowadzenie wzorów dla parametrów ar, br oraz as i bs. Problem rozwiązywany jest na dwa sposoby:
1. Stosuje się przybliżone oszacowane parametrów regresji stosując metody numeryczne, z których najbardziej znane to metoda Gaussa-Newtona i Marquardta (obie dają ten sam wynik liczbowy o ile jest on prawidłowy). Obie wymagają dużo obliczeń (nawet napisanie programu wyliczającego takie parametry jest pracochłonne), ale na szczęście należą do standardów. W Internecie jest wiele darmowych programów pozwalających na ich wyliczenie.
2. Stosuje się tzw. linearyzację funkcji należących do danej rodziny, co oznacza w przypadku rozważanych trzech rodzin funkcji takie przekształcenia, aby uzyskać równość F(y)=ax+b. Dla regresji logistycznych jest są to funkcje: ar*N+br=-log((1-pr)/pr) i as*N+bs=-log((1-ps)/ps)). Dla regresji arcustangensowych są to funkcje ar*N+br=tan(pi*(pr-0.5)) i as*N+bs=tan(pi*(ps-0.5)). Dla regresji Gompertza są to funkcje ar*N+br=-log(-log(pr)) oraz as*N+bs=-log(-log(ps)). Po takiej transformacji wartości pr i ps uzyskanych eksperymentalnie możemy wyliczać zwykłą regresję liniową między liczebnością populacji a uzyskanymi danymi.
W zależności od wyboru regresji i metody oszacowania jej parametrów dla takiego samego zestawu danych możemy uzyskać w sumie 16 różnych funkcji. Przykładowo dla danych pokazanych na początku rozdziału uzyskujemy następujące wartości.
| Rodzaj regresji | Metoda najmniejszych kwadratów | Linearyzacja | ||||||
| ar | br | as | bs | ar | br | as | bs | |
| liniowe | -0.0091 | 1.0443 | 0.0096 | -0.0071 | – | – | – | – |
| logistyczne | -0.0438 | 2.6373 | 0.0468 | -2.5115 | -0.0462 | 2.8088 | 0.0447 | – 2.3861 |
| arcustangensowe | -0.0398 | 2.4062 | 0.0437 | -2.3590 | -0.0578 | 3.578 | 0.0454 | – 2.4683 |
| Gompertza | -0.0329 | 2.4004 | 0.0303 | -1.2157 | -0.0378 | 2.7051 | 0.0301 | – 1.1555 |
Do szacowania nieliniowych regresji metodą najmniejszych kwadratów zastosowano procedury w programie SAS. Program ten operuje rozbudowanym algorytmem Marquardta, który w dużym stopniu uniezależnia otrzymywanie wyniku od wartości początkowych parametrów. Polecam go bo inne programy z reguły pokazują błędne wyniki, zwłaszcza dla regresji logistycznej.
Łatwo się przekonać, że wykresy wszystkich regresji nieliniowych między N a pr oraz wszystkich regresji między N a ps w dużym stopniu się pokrywają i nie różnią się zasadniczo od odpowiedniej regresji liniowej.
Zadania dla studentów
- Przenieść kod programu najprostszej populacji z mechanizmem regulacyjnym do Pythona. Wprowadzać do niego różne wzory na prawdopodobieństwa rozrodu i śmierci. Uruchomić Pythona i poczekać na plik tekstowy ‘wyniki.txt’.
- Przenieść wyniki do Excela lub arkusza kalkulacyjnego, tak by poszczególne wielkości (powtórzenie, czas, liczebność) były w osobnych kolumnach. Należy w tym celu uruchomić Excela lub Calca. Otworzyć nowy plik i wybrać opcję tekstowy. Otworzyć ‘wyniki.txt’. Pojawią się opcje umożliwiające rozdzielenie kolumn.
- Liczebności populacji z kolejnych powtórzeń przenieść obok siebie (tak by określonemu momentowi czasowemu odpowiadało 10 różnych liczebności uzyskanych podczas 10 powtórzeń właśnie w tym momencie). Wykonać wykres zależności poszczególnych dynamik od czasu. Zatytułować go. Obowiązkowo podpisać osie.
- Zmodyfikować kod programu, tak aby występowały w nim funkcje logistyczne z parametrami wyliczonymi metodą Marquardta. Oznacza to zmianę parametrów na wyliczone oraz zmianę kodu w jednym miejscu w dwóch linijkach, gdzie definiuje się pr i ps.
- Wykonać program, przenieść dane do Excela lub arkusza kalkulacyjnego, zrobić wykres 10 dynamik liczebności. Zatytułować go “Wzory logistyczne, metoda Marquardta” lub bardziej szczegółowo, obowiązkowo podpisać osie.
- Opisane operacje powtórzyć dla parametrów uzyskanych poprzez linearyzację, a następnie inne rodziny funkcji.
- Ocenić różnice między wykresami zwracając uwagę na to, wokół jakich wartości wahają się dynamiki, jaka jest amplituda tych wahań oraz czas po jakim następuje wzrost populacji, a następnie już tylko wahania wokół jednej wartości. Można to ocenić wizualnie albo wymyślając jakąś odpowiednią charakterystykę liczbową.
- Odpowiedzieć na pytania:
- Czy jest konieczne stosowanie jakiś wzorów na prawdopodobieństwo rozrodu i śmierci osobnika w modelu populacji?
- Czy wyniki modelowania zależą od rodziny funkcji jaką założono przy wyliczaniu regresji między liczebnością a prawdopodobieństwem rozrodu albo śmierci osobnika?
- Czy stosowanie innych rodzin funkcji tworzy nam inny model populacji (modele liniowe, logistyczne, arcustangensowe, Gompertza)?
- Co tracimy ograniczając się do tworzenia tylko modeli logistycznych? Jakie warunki powinny spełniać parametry ar, br, as i bs aby uzyskiwać modele w miarę trwałych populacji? .