Liczby

Typy liczb

 

Liczby zapisywane są w komputerze w bajtach za pomocą dwóch sposobów kodowania binarnego. Liczby całkowite zapisywane są w kodowaniu prostym w taki sam sposób jak liczby w systemie dwójkowym. Jeżeli system liczbowy jest podany jako indeks dolny z prawej strony liczby to:

0₁₀=0₂, 1₁₀=1₂, 2₁₀=10₂, 3₁₀=11₂, 4₁₀=100₂ itd.

Liczby całkowite zapisywane są przy zastosowaniu kodowania prostego po uprzednim przekształceniu ich na zapis w systemie binarnym. W języku maszynowym 0 to brak przepływu prądu, 1 to przepływ prądu, 0 to brak namagnesowania pamięci operacyjnej, 1 to namagnesowanie, a w komputerach lampowych 0 to zgaszona lampa elektronowa, a 1 to zapalona lampa elektronowa, czyli brak sygnału (0) i sygnał (1). Pierwszy bit z lewej strony obszaru przeznaczonego na zapis liczby przeznaczony jest na znak liczby. Brak sygnału to liczba dodatnia, a sygnał oznacza liczbę ujemną. W 16-bitowym bajcie można zatem zapisać liczby od 1111111111111111₂ do 0111111111111111₂, czyli od -32767₁₀ do 32767₁₀. To bardzo często zbyt mało, ale już zapis takich liczb w 32 bitowym bajcie lub 64-bitowym bajcie obejmuje wystarczający zakres liczb całkowitych do wielu obliczeń. W Pythonie istnieje także możliwość definiowania liczb całkowitych dowolnie dużych. W nowych wersjach programu jest to już standard. Mają one nie ustalony z góry zakres obszaru, w którym są zapisywane. Gdy trzeba zapisać liczbę odpowiednio większą od poprzedniej, ilość bitów na jej zapis ulega zwielokrotnieniu.

Zupełnie inaczej koduje się liczby rzeczywiste. są one przekształcane na zapis dwójkowy i zapisywane w notacji zmiennoprzecinkowej z kodowaniem z nadmiarem. Każdą liczbę rzeczywistą x można w jednoznaczny sposób zapisać w postaci:

x = znak·2^{Cecha-Nadmiar}·Mantysa

gdzie znak ma wartość + (brak sygnału) lub – (sygnał), cecha jest liczbą całkowitą (zapisaną w 8 bitach dla liczb pojedynczej precyzji i w 11 bitach dla liczb podwójnej precyzji, nadmiar jest stałą (równą 127 dla liczb pojedynczej precyzji, 1023 dla liczb podwójnej precyzji), mantysa jest liczbą z przedziału [1,2) zapisaną w postaci 1.1100101110001010111, gdzie ciąg zer i jedynek po kropce odpowiednio dobiera się by dostać liczbę możliwie najbliższą x. Liczba 1 przed kropką jest zawsze i w komputerze nie trzeba jej kodować. Cechę i Mantysę wyliczymy dla każdej liczby x w sposób jednoznaczny po przyjęciu odpowiedniego sposobu ich zapisu (pojedynczej lub podwójnej precyzji). Natomiast w komputerze koduje się tylko zera (braki sygnału) i jedynki (sygnały) znaku, cechu i części ułamkowej mantysy.

Zarówno przy kodowaniu prostym jak i zmiennoprzecinkowym maszyna ma zapis w bajtach tylko zer i jedynek. Zatem przed wykonaniem jakiś działań na liczbach najczęściej trzeba poinformować program jaki jest typ liczby. Dotyczy to obowiązkowo takich języków programowania, jak C++ i Pascal. Natomiast Python i R nadają liczbom typ domyślny po sposobie jej zapisu (z kropką lub bez) i rodzaju działań. Do programu wpisujemy liczbę w systemie dziesiętnym. Zostaje ona domyślnie przekształcona na liczbę o określonym typie. W Pythonie typ prosty, zapisywany w 32 bitowym bajcie, nazywany jest int. Typ zmiennoprzecinkowy to typ liczb podwójnej precyzji zapisywanych w 64 bitach (dwóch bajtach 32-bitowych lub jednym 64-bitowym) nazywany jest float. Poza zupełnie różnym kodowaniem liczb o typie int i float, stosuje się dla nich zupełnie inne algorytmy dodawania liczb, odejmowania, mnożenia i dzielenia. Typ liczby odkryjemy za pomocą funkcji type().

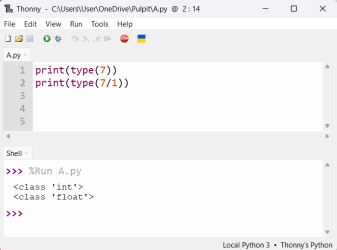
W Idle Pythona można wpisać type(7) i nacisnąć enter. Poniżej pojawi się wynik. W Thony, by uzyskać wyniki w oknie Shell, należy użyć funkcji print(…). Następnie należy kliknąć na biały trójkącik w zielonym kółeczku. Jest to uruchamianie skryptu (Run current script). To samo uzyskamy naciskając klawisz F5. Wygląda to następująco:

Aby nie pokazywać instrukcji wykonywanych przez program Thonny w sposób graficzny, dalej tego typu instrukcje i programy pokazywane będą w tabelach postaci:

print(type(7)) print(type(7.2))

>>> <class ‘int’> <class ‘float’>

Prosty sposób kodowania liczby całkowitej można zamienić funkcją float(n). Powstaje przybliżenie liczby 7 zapisane zmiennoprzecinkowo. Operacja odwrotna wykonywana jest funkcją int(x) i poprzedzona jest pominięciem części ułamkowej liczby x.

print(int(7.9)) print(float(7))

>>> 7 7.0

Liczby można zapisać także w systemie szesnastkowym (zapis z dwuznakiem 0x lub 0X na początku). Interpreter Pythona zwraca te liczby w systemie dziesiętnym.

print(0x25) print(0XAB) print(0xAB/0X25)

>>> 37 171 4.621621621621622

Tego typu liczby są używane w kodowaniu kolorów w systemie RGB.

 

Działania na liczbach

W IDLE Pythona można wpisywać działania na liczbach i po naciśnięciu Enter pojawi się wynik. W Thonny, aby uzyskać wyniki działań na liczbach i użyć funkcji print() z nawiasami. Dodawanie, mnożenie, odejmowane i dzielenie wygląda następująco:

print(7+2) print(7*2) print(7-2) print(7/2)

>>> 9 14 5 3.5

Podnoszenie do potęgi wykonywane jest za pomocą dwuznaku ‘**’.

print(2**1, 2**2, 2**3, 2**4, 2**5) print(3**1, 3**2, 3**3, 3**4, 3**5) print(1**0.5, 2**0.5, 3**0.5, 4**0.5, 9**0.5) print(1**-0.5, 2**-0.5, 3**-0.5, 4**-0.5, 9**-0.5)

>>> 2 4 8 16 32 3 9 27 81 243 1.0 1.4142135623730951 1.7320508075688772 2.0 3.0 1.0 0.7071067811865476 0.5773502691896257 0.5 0.3333333333333333

Natomiast stosowanie tzw. karetki (znaku ‘^’) nie jest potęgowaniem. W starych wersjach Pythona symbol ten generował błąd, w nowych daje dość zaskakujące wyniki:

print(2^1, 2^2, 2^3, 2^4, 2^5, 2^6, 2^7, 2^8, 2^9, 2^10) print(3^1, 3^2, 3^3, 3^4, 3^5, 3^6, 3^7, 3^8, 3^9, 3^10) print(4^1, 4^2, 4^3, 4^4, 4^5, 4^6, 4^7, 4^8, 4^9, 4^10) print(5^1, 5^2, 5^3, 5^4, 5^5, 5^6, 5^7, 5^8, 5^9, 5^10)

>>> 3 0 1 6 7 4 5 10 11 8 2 1 0 7 6 5 4 11 10 9 5 6 7 0 1 2 3 12 13 14 4 7 6 1 0 3 2 13 12 15

Okazuje się, że to działanie zwraca liczbę pokazującą, w ilu bitach i na której pozycji binarne zapisy liczby z lewej różnią się od liczby z prawej. Jej wynik powstaje w ten sposób, w najpierw tworzy się liczbę binarną, np. 1001101 w która powstaje z różnic między binarnym zapisem liczb (1 oznacza różnicę, 0 brak różnic) na kolejnych pozycjach. Potem tę liczbę zapisuje się w systemie dziesiętnym (dla przykładu 1001101₂=1+4+8+64=79) i to jest wynik działania n^k.

Dzielenie z resztą liczb n przez m to znajdywanie takich liczb całkowitych k i r, że n = m*k + r oraz liczba r jest mniejsza od m. Wszystko to ma sens, gdy liczby n i m są całkowite i dodatnie. W Pythonie liczbę k znajduje się stosując dwuznak //, natomiast r, zwany resztą, wyliczymy stosując symbol ‘%’.

print(15//2, 15//3, 15//4, 15//5) print(15%2, 15%3, 15%4, 15%5)

>>> 7 5 3 3 1 0 3 0

Sprawy się trochę komplikują, gdy tą samą regułę zastosujemy do liczb ujemnych:

print(15//-2, 15//-3, 15//-4, 15//-5) print(15%-2, 15%-3, 15%-4, 15%-5) print() print(-15//2, -15//3, -15//4, -15//5) print(-15%2, -15%3, -15%4, -15%5) print() print(-15//-2, -15//-3, -15//-4, -15//-5) print(-15%-2, -15%-3, -15%-4, -15%-5)

>>> -8 -5 -4 -3 -1 0 -1 0-8 -5 -4 -3 1 0 1 07 5 3 3 -1 0 -3 0

Za każdym razem reszta jest bliższa 0 niż dzielnik, a wynik dzielenia odpowiednio dopasowany, by reguła km+r=n była spełniona. Reguła ta została rozciągnięta na liczby rzeczywiste:

print(15.3//2.7, 15.3//-2.7, -15.3//2.7, -15.3//-2.7) print(15.3%2.7, 15.3%-2.7, -15.3%2.7, -15.3%-2.7)

>>> 5.0 -6.0 -6.0 5.0 1.7999999999999998 -0.9000000000000004 0.9000000000000004 -1.7999999999999998

Istotne jest tylko to, aby wynik x//y był liczbą całkowitą (choć kodowaną jako zmiennoprzecinkowa), a reszta z dzielenia była bliższa zeru niż y i spełnione było równanie km+r=n.

 

Kolejność wykonywania działań

W przypadku, gdy pomiędzy liczbami pojawi się więcej niż jeden symbol działania, obowiązuje ściśle określona kolejność ich wykonywania. Reguły je opisujące są takie same jak w matematyce. Można je streścić w 5 zasadach:

1. Najwyższy priorytet mają wyrażenia objęte nawiasami okrągłymi. Są one wykonywane w pierwszej kolejności.

print(1-2+3, (1-2)+3, 1-(2+3)) print(1/2*3, (1/2)*3, 1/(2*3))

>>> 2 2 -4 1.5 1.5 0.16666666666666666

2. Spośród działań nie objętych nawiasami najwyższy priorytet ma potęgowanie. Jest ono wykonywane na początku, a pozostałe działania dotyczą już jego wyniku.

print(1+2**3, 1+(2**3), (1+2)**3) print(2*3**3, 2*(3**3), (2*3)**3)

>>> 9 9 27 54 54 216

3. Mnożenie i dzielenie mają ten sam priorytet i działania wykonywane są w kolejności od lewej do prawej.

print(1/2*3, (1/2)*3, 1/(3*2))

>>> 1.5 1.5 0.16666666666666666

4. Mnożenie i dzielenie mają wyższy priorytet od dodawania i odejmowania.

print(1+2*3, (1+2)*3, 1+(2*3)) print(1-2*3, (1-2)*3, 1-(2*3)) print(1+2/3, (1+2)/3, 1+(2/3)) print(1-2/3, (1-2)/3, 1-(2/3))

>>> 7 9 7 -5 -3 -5 1.6666666666666665 1.0 1.6666666666666665 0.33333333333333337 -0.3333333333333333 0.33333333333333337

 

5. Dodawanie i odejmowanie mają ten sam priorytet i wykonywane są w kolejności od lewej do prawej

print(1-2+3, (1-2)+3, 1-(2+3))

>>> 2 2 -4

 

Gdy ktoś nie jest pewny, w jakiej kolejności Python wykona działania, może stosować dowolną liczbę nawiasów okrągłych wskazującą na właściwą kolejność działań, nawet wtedy gdy nie jest to konieczne.

 

Relacje między liczbami

Relacja równości w Pythonie ma inny symbol niż w matematyce. Jest nią dwuznak “==”. w starszych wersjach programu stosowane było także ‘is’. Relacja nierówności oznaczana jest dwuznakiem “!=” albo ‘is not’. W nowych wersjach Pythona może pojawić się na czerwono komunikat, że formy ‘is’ i ‘is not’ są przestarzałe.

print(7==7,7==17) print(7 is 7, 7 is 17) print(7 != 7, 7 != 17) print(7 is not 7, 7 is not 17)

>>> True False True False False True False True

Najczęściej stosowanymi relacjami dla liczb są cztery typy porównań wielkości liczb (o symbolach ‘<‘, ‘<=’, ‘>’, ‘>=’). Stosuje się je tak jak działania, wstawiając symbol relacji między liczby, a w wyniku otrzymujemy wartość logiczną ‘False’ albo ‘True’. Wygląda to następująco:

print(7<7, 7<17) print(7<=7, 7<=17) print(7>7, 7>17) print(7>=7, 7>=17)

>>> True False False True True True False False True False

 

Funkcje matematyczne

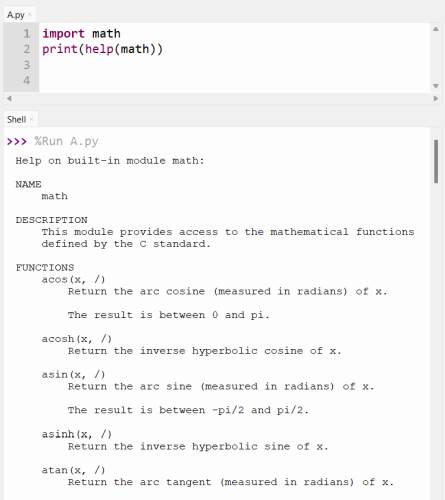
Podstawową zaletą komputera jest możliwość obliczeń funkcji matematycznych dla dowolnych wartości należących do dziedziny funkcji. Uczymy się ich na matematyce, ale dopiero na studiach okazuje się, że są one potrzebne do rozwiązania różnych czysto biologicznych problemów. Większość tych funkcji znajduje się w bibliotece ‘Math’, która należy zaimportować do programu. Za pomocą funkcji help(math) możemy obejrzeć, jakie funkcje zawiera ta biblioteka:

Załadowanie biblioteki math wykonuje się za pomocą komendy import. Zawartość tej biblioteki w aneksie 3. W tabeli pokazano dwa sposoby korzystania z niej. Wygląda to następująco:

import math print(math.factorial(7)) print(math.sin(math.pi/7)) print(math.log(2**1024+1)) print(math.exp(2**1024+1))	from math import factorial, sin, log, exp, pi print(factorial(7)) print(sin(pi/7)) print(log(2**1024+1)) print(exp(2**1024+1))
>>> 5040 0.4338837391175581 709.782712893384 Traceback (most recent call last):   File “C:\Users\User\OneDrive\Pulpit\A.py”, line 5, in     print(exp(2**1024+1)) OverflowError: int too large to convert to float	>>> 5040 0.4338837391175581 709.782712893384 Traceback (most recent call last):   File “C:\Users\User\OneDrive\Pulpit\A.py”, line 5, in     print(exp(2**1024+1)) OverflowError: int too large to convert to float

W obu programach w oknie wyników pojawią się te same informacje, łącznie z tym, że argument funkcji exp() jest za duży. Funkcja factorial() liczy silnię argumentu, którym musi być liczba całkowitą.

Wykaz wszystkich funkcji znajdujących się w bibliotece math:

acos(x) – arcus cosinus(x) dla x z przedziału [-1,1], wyniki w radianach.
acosh(x) – arcus cosinus hiperboliczny.
asin(x) – arcus simus(x) dla x z przedziału [-1,1], wyniki w radianach.
asinh(x) – arcus sinus hiperboliczny.
atan(x) – arcus tangens(x), wyniki w radianach.
atan2(y,x) – arcus tangens(y/x), wyniki w radianach.
atah(x) – arcus tangens hiperboliczny.
ceil(x) – zaokrąglenie w górę do liczby całkowitej.
comb(n,k) – liczba kombinacji k-elementowych wybieranych ze zbioru n-elementowego.
copysign(x,y) – liczba równa wartości bezwzględnej x ze znakiem y.
cos(x) = cosinus x.
cosh(x) – cosinus hiperboliczny x.
degrees(x) – konwersja x w radianach na wielkość w stopniach.
dist(p,q) – odległość euklidesowa między punktami p i q z przestrzeni n-wymiarowej zapisane jako listy jednakowej długości.
erf(x) – bład w x.
erfc(x) – komplementarny bład w x.
exp(x) – stała e w potędze x.
expm1(x) = exp(x)-1.
fabs(x) – wartość bezwzględna z x.
factorial(x) = x! (silnia z x).
floor(x) – zaokrąglenie x do całkowitej w dół.
fmod(x) – ?
frexp(x) – mantysa exp(x) zapisana jako (m,e), gdzie m jest rzeczywiste, e całkowite.
fsum(seq) – suma liczb w podanym ciągu.
gamma(x) – funkcja gamma.
gcd(x,y), gcd(x1,x2,…,) – wylicza największy wspólny dzielnik.
hypot(p) – odległość euklidesowa od 0 dla punktu p wrażonego współrzędnymi.
isclose(a,b)- sprawdza podobieństwo liczb.
isfinite(x) – sprawdza czy x nie jest równe None lub Inf.
isinf(x) – sprawdza czy x jest równe Inf lub -Inf.
isnan(x) – sprawdza czy x jest równe NaN (not a number).
isqrt(x) – część całkowita pierwiastka z x.
lcm(x,y), lcm(x1,x2,…) – najmniejsza wspólna wielokrotność.
lgama(x) – logarytm funkcji gamma.
log(x) – logarytm naturalny x.
log10(x) – logarytm dziesiętny x.
log1p(x) – logarytm naturalny z x+1.
log2(x) – logarytm o podstawie 2 z x.
modf(x) – częsć ułamkowa i całkowita liczby x.
nextafter(x, y) – następny punkt po x w kierunku punktu y.
perm(n,k) – liczba różnoelementowych ciągów k-elementowych, którą można utworzyć z n różnych elementów. pow(x,y) – potęga y liczby x = x**y.
prod(x1,x2,…) – iloczyn liczb w nawiasie.
radians(x) – konwersja kata x w stopniach na wielkość w radianach.
remainder(x,y) – najmniejsza dodatnia różnica między x a ny dla różnych całkowitych n.
sin(x) – sinus liczby x.
sinh(x) – sinus hiperboliczny liczby x.
sqrt(x) – pierwiastek x.
tan(x) – tangens x.
tanh(x) – tangens hiperboliczny x.
trunc(x) – zaokrąglenie w dół dla liczb dodatnich i w górę dla liczb ujemnych do liczby całkowitej.
ulp(x) – najmniejszy istotny bit liczby zmiennoprzecinkowej x.

Stałe matematyczne

 

Biblioteka ‘math’ obok funkcji zawiera jeszcze stałe matematyczne. Są nimi liczba π (około 3.14), stała Eulera e (około 2.71), oraz stała τ=2⋅π (około 6.28).

import math print(math.e) print(math.pi) print(math.tau)

>>> 2.718281828459045 3.141592653589793 6.283185307179586

Stała τ jako stosunek obwodu koła do jego promienia uważana jest przez niektórych nauczycieli matematyki w USA jako bardziej naturalna i intuicyjna niż stała π. Przedstawiam to jako ciekawostkę, bo sama tak nie uważam, a przynajmniej nie uważam to na tyle ważne, by stosować dla 2⋅π osobną nazwę i oznaczenie.

 

Liczby zespolone

 

Jeżeli uświadomimy sobie, że liczby, począwszy od całkowitych dodatnich (oceny liczności zbiorów) poprzez liczby ujemne (oceny stanów konta) do liczb rzeczywistych (miary długości, objętości, ciężaru i wielu innych zmiennych ciągłych) istnieją tylko w takim samym sensie jak litery A, C, G i T na genomach wszystkich eukariotów, to dopuszczenie do takiego istnienia liczb zespolonych nie będzie stanowiło psychicznego problemu. Są to symboliczne określenia służące do analizy zjawisk występujących już nie w samej przyrodzie, ale w obrębie wiedzy o rzeczywistości.

Liczby zespolone coraz częściej pojawiają się w biologii, najczęściej w algorytmach umożliwiających odwracanie macierzy lub inne obliczenia na złożonych grupach danych. W Pythonie liczby te zapisuje się, jako sumę liczb rzeczywistej i urojonej, gdzie urojoną jest liczbą z dopisanym j. Liczby zespolone są uogólnieniem liczb rzeczywistych gdyż liczby typu x+0j traktować można jako liczby rzeczywiste. Działania na tych liczbach wykonuje się dokładnie tak, jak działania na wielomianach z niewiadomą x (której rolę pełni j), przy czym j²=-1. Definiuje się dla nich takie same działania i funkcje, jakie są zdefiniowane dla liczb rzeczywistych. Gdy część urojona liczb jest równa 0, to wynik działań jest taki sam, jakby wykonywało się to działanie na liczbach rzeczywistych.

print((23.7+0.2j)+(2-0.3j)) print((23.7+0.2j)-(2-0.3j)) print((23.7+0.2j)*(2-0.3j)) print((23.7+0.2j)/(2-0.3j)) print((23.7+0.2j)**(2-0.3j))

>>> (25.7-0.09999999999999998j) (21.7+0.5j) (47.46-6.709999999999999j) (11.574572127139364+1.8361858190709046j) (335.41805825358085-452.36821998064454j)

Prawie zawsze po wykonaniu programu dla liczb zespolonych (który bywa krótszy i efektywniejszy od analogicznego, napisanego dla liczb rzeczywistych) chcemy odczytać wartość rzeczywistą lub urojona wyniku. Nie robi się to funkcją, ale tzw. metodą poprzez dopisanie po kropce frazy .real albo .imag.

print((23.7+0.2j).real) print((23.7+0.2j).imag)

>>> 23.7 0.2

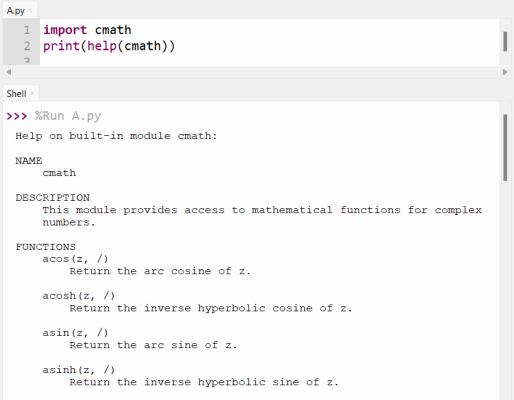
Funkcje zespolone są definiowane także jako uogólnienia takich samych funkcji określonych dla liczb rzeczywistych. Przeważnie posiadają też takie same właściwości. Ich definicje są wynikiem pracy wielu wybitnych osiemnastowiecznych i dziewiętnastowiecznych matematyków. W Pythonie są one zgromadzone w bibliotece cmath. Jej zawartość można zobaczyć po wpisaniu instrukcji print(help(cmath)) po uprzednim zaimportowaniu biblioteki cmath.

import cmath print(help(cmath))

Początek opisu tej biblioteki wygląda następująco:

Korzystanie z tej biblioteki jest niemal identyczne jak korzystanie z biblioteki math.