Przegląd podrzędnych funkcji graficznych
Wykaz podrzędnych funkcji graficznych
Funkcje graficzne podrzędne, zwane inaczej dokładającymi, same z siebie nie tworzą wykresu. Służą do nakładania na wykres znajdujący się w aktywnym oknie różnych elementów. W podstawowym pakiecie graphics są to:
- Funkcje dokładające serie danych w postaci punktów lub linii:
- points()
- lines()
- abline()
- Funkcje dokładające tekst:
- text()
- mtext()
- title()
- Funkcje dokładające zasadnicze części wykresu (osie, legendę, obramowania, siatkę):
- axis()
- rug()
- legend()
- box()
- grid()
- Funkcje dokładające pozwalające na narysowanie na wykresie mniej lub bardziej złożonych figur geometrycznych:
- segments()
- arrows()
- rect()
- polygon()
Wszystkie te funkcje wymagają określenia miejsca, gdzie ma pojawić się określony element. Większość posługuje się współrzędnymi pola kreślenia, ale są też funkcje posługujące się numerem marginesu i numerem linijki określającej odległość na danym marginesie od pola kreślenia. Funkcje box() i grid() odczytują położenie pola kreślenia, nie mają zatem współrzędnych obowiązkowych.
Funkcje posługujące się współrzędnymi pola kreślenia używają nazw zaczynających się od x na współrzędne odczytywane na osi poziomej i y na współrzędne odczytywane na osi pionowej. Są to początkowe argumenty funkcji graficznych podrzędnych i wstawiając odpowiednie wartości na właściwym miejscu ich formalne nazwy można pominąć. Wykaz nazw formalnych argumentów funkcji graficznych podrzędnych posiłkujących się bezpośrednio lub pośrednio współrzędnymi pola kreślenia pokazuje następująca tabela:
Funkcja i jej obowiązkowe argumenty |
Uwagi |
points(x,y) |
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
lines(x,y) |
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
abline(b,a) |
a,b - współczynniki prostej ax+b wykreślanej w polu kreślenia. |
text(x,y,tekst) |
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, tekst - wektor tekstowy, długości wektorów x,y,tekst muszą być równe. |
legend(x,y,tekst) |
x - współrzędna na osi poziomej, y - współrzędna na osi pionowej, tekst - wektor tekstowy, Wektory x i y muszą być jednoelementowe. |
segments(x0, y0, x1, y1) |
x0 - wektor współrzędnych na osi poziomej, y0 - wektor współrzędnych na osi pionowej, x1 - wektor współrzędnych na osi poziomej, y1 - wektor współrzędnych na osi pionowej, długości wektorów x0, y0, x1, y1 muszą być równe. |
arrows(x0, y0, x1, y1) |
x0 - wektor współrzędnych na osi poziomej, y0 - wektor współrzędnych na osi pionowej, x1 - wektor współrzędnych na osi poziomej, y1 - wektor współrzędnych na osi pionowej, długości wektorów x0, y0, x1, y1 muszą być równe. |
rect(xleft, ybottom, xright, ytop) |
xleft - wektor współrzędnych na osi poziomej, ybottom - wektor współrzędnych na osi pionowej, xright - wektor współrzędnych na osi poziomej, ytop - wektor współrzędnych na osi pionowej, długości wektorów xleft, ybottom, xright, ytop muszą być równe. |
polygon(x,y) |
x - wektor współrzędnych na osi poziomej, y - wektor współrzędnych na osi pionowej, długości wektorów x i y muszą być równe. |
Wszystkie wymienione funkcje nie dają żadnej informacji o tym, że użyte współrzędne nie mieszczą się w wykreślonym polu kreślenia lub na całym wykresie. Po prostu nie rysują na wykresie tego, co się na nim nie mieści.
Wykaz nazw formalnych argumentów funkcji graficznych podrzędnych posiłkujących się numerami marginesu i linijki pokazuje następująca tabela:
Funkcja i jej obowiązkowe argumenty |
Uwagi |
axis(side) |
side - jedna z liczb 1, 2, 3, 4 pokazująca, na której krawędzi pola kreślenia ma być umiejscowiona oś. |
rug(x, ticksize, side) |
x - wektor punktów, ticksize y - długość znacznika, side jedna z liczb 1,2,3,4 pokazująca, na której osi maja byc znaczniki. |
mtext(text, side, line) |
text - zmienna tekstowa side - jedna z liczb 1,2,3,4 pokazująca, na którym marginesie ma się pokazać tekst, line - linijka, w której ma sie pokazać tekst. |
title(main, sub,
xlab, ylab, line)
|
main="tekst" oznacza tekst napisany na marginesie górnym sub="tekst" oznacza tekst napisany na marginesie dolnym, xlab="tekst" oznacza tekst napisany na marginesie dolnym, ylab="tekst" - oznacza tekst napisany na marginesie lewym, line oznacza linijke tekstu, w której napisany będzie tekst. |
Zastosowanie funkcji points(), lines(), text(), mtext(), title(), axis(), rug(), legend(), box() i grid() zostało już pokazane w poprzednich rozdziałach. Funkcja abline() będzie pokazana w rozdziale o liniach trendu i regresji liniowej. W dalszej części pokazano zastosowanie pozostałych podrzędnych funkcji graficznych wymienionych w wykazie na początku rozdziału.
Funkcja segments()
Funkcja segments() umożliwia narysowanie na wykresie odcinka jednego lub kilku. Jej obowiązkowymi argumentami są współrzędne punktu początkowego odcinka x0, y0 i współrzędne punktu końcowego odcinka x1 i y1. Wielkości x0, y0, x1 i y1 mogą być wektorami o jednakowej długości i wtedy funkcja segments() wykreśli tyle odcinków, ile jest liczb w każdym z tych wektorów. Pierwsze liczy tych wektorów określają współrzędne końców odcinka pierwszego, drugie to współrzędne końców odcinka drugiego itd.
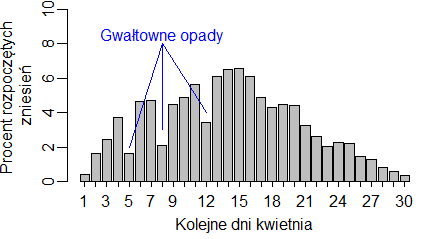
segments(x0, y0, x1, y1, col=”black”, lty=1, lwd=1)Zdarza się, że na jakiś wykresach chcemy wskazać szczególne punkty i je dodatkowo objaśnić. Wtedy objaśnienie umieszczany w wolnym miejscu na wykresie, a funkcja segment wykreślamy odcinki od objaśnienia do określonych elementów wykresu. Tak jak to pokazano na poniższym wykresie charakteryzującym sezon lęgowy mazurków (dla 250 gniazd kontrolowanych przez wszystkie dni kwietnia określono dzień, w którym zostało zniesione pierwsze jajo).
x=c(0.41, 1.63, 2.44, 3.75, 1.63, 4.64, 4.72, 2.12, 4.48, 4.89, 5.62, 3.42,
6.11, 6.51, 6.60, 6.11, 4.89, 4.32, 4.48, 4.40, 3.26, 2.61, 2.04, 2.28,
2.20, 1.47, 1.30, 0.81, 0.57, 0.33)
windows(4.5, 2.5)
par(mar=c(3,3.5,0.5,0.5), mgp=c(1.7, 0.5, 0))
a=barplot(y, ylim=c(0,10),xlab="Kolejne dni kwietnia",
ylab="Procent rozpoczętych \nzniesień")
axis(1, at=a, labels=1:30, tck=-0.03)
segments(c(a[8],a[8],a[8]),c(8,8,8),c(a[5],a[8],a[12]),c(2,3,4), col="blue")
text(a[8], 8.5, "Gwałtowne opady", col="blue")
|
Program ten generuje następujący wykres:
W programie tym wykorzystano fakt, że funkcja barplot() obok wykresów generuje też współrzędne punktów będące środkami wykreślonych słupków.
Funkcja arrows()
Funkcja arrows(), jak sama nazwa wskazuje, umieszcza na wykresie strzałki, czyli odcinki zakończone grotem, narysowanym jako para segmentów o jednakowej długości wychodzących z końca odcinka i nachylonych do niego pod tym samym kątem. Przypomina ona nieco funkcję segments(), gdyż jej obowiązkowymi parametrami są współrzędne początku x0, y0 i współrzędne końca x1, y1 strzałki. Mogą to być wektory, gdy w programie należy narysować kilka strzałek. Pierwsze liczby tych wektorów określają współrzędne końców pierwszej strzałki, drugie – to współrzędne końców odcinka drugiej strzałki itd.
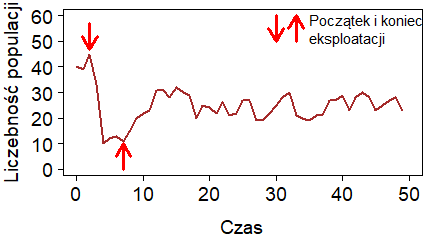
Strzałki mogą wskazywać na te punkty wykresu, które trzeba wyjaśnić lub opisać. Przykładowo, poniższy wykres pokazuje dynamikę liczebności populacji, na której wykonano eksperyment polegający na wyławianiu osobników i wypuszczaniu ich w odległości 20 km.
N=c(40, 39, 45, 33, 10, 12, 13, 11, 15, 20, 22, 23, 31, 31, 28, 32, 30, 29,
20, 25, 24, 22, 26, 21, 22, 27, 27, 19, 19, 22, 25, 28, 30, 21, 20, 19, 21, 21,
27, 27, 29, 23, 28, 30, 28, 23, 25, 27, 28, 23)
windows(4.5, 2.5)
par(mar=c(3.3,3.3,0.5,0.5),mgp=c(2.2,0.5,0),las=1,xpd=TRUE, ps=14)
plot(0:49,N, type="l", col="brown", lty=1, lwd=2,
xlab="Czas", xlim=c(0,50), ylab="Liczebność populacji",
ylim=c(0,60), tck=-0.03, las=1)
arrows(c(2,30),c(57,60),c(2,30),c(47,50),col="red", length=0.15, lwd=3)
arrows(c(7,33),c(0,50),c(7,33),c(10,60), col="red", length=0.15, lwd=3)
text(35,55, "Początek i koniec \neksploatacji", adj=0, cex=0.8)
|
Wykres wykonany za pomocą tego programu wygląda następująco:
Do interesujących opcji funkcji arrows() należy length=x określająca długość ramion tworzących grot, angle=x określająca kąt w stopniach między ramionami grota a osią strzałki (domyślnie 30°), oraz code=n przyjmujący wartości 1, 2 i 3 przy czym
- code=1 oznacza że grot utworzy się na końcu (x1, y1)
- code=2 oznacza, że grot utworzy się na końcu (x0, y0)
- code=3 oznacza, że grot utworzy się na obu końcach
Poza tym działają w niej te opcje graficzne, które związane są z grubością i stylem linii.
Funkcja rect()
Funkcja rect() służy do rysowania prostokątów na wykresie. Jej obowiązkowymi opcjami są współrzędne dolnego lewego rogu i współrzędne górnego prawego rogu. Była już wykorzystywana do kolorowania pola kreślenia i najczęściej w tym celu się ją stosuje – aby zaznaczyć obszary interesujących danych. Ponieważ jednak funkcja rect() zamazuje przed nią wprowadzane dane, trzeba je dołożyć (najczęściej ponownie) po jej zastosowaniu.
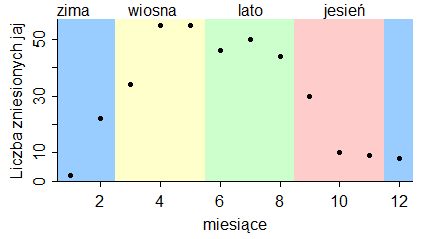
Liczba jaj znoszona przez pewną populację gołębi miejskich w ciągu roku mogłaby być narysowana następująco:
x=c(2, 22, 34, 55, 55, 46, 50, 44, 30, 10, 9, 8)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03)
plot(1:12, x, pch=20, xlab="miesiące", ylab="Liczba zniesionych jaj", main="")
rect(0.59,0,2.5, 70, col="#99ccff", border=NA)
rect(2.5,0,5.5, 70, col="#ffffcc", border=NA)
rect(5.5,0,8.5, 70, col="#ccffcc", border=NA)
rect(8.5,0,11.5, 70, col="#ffcccc", border=NA)
rect(11.5,0,12.5,70, col="#99ccff", border=NA)
points(1:12, x, pch=20)
mtext("zima",3,0, adj=0)
mtext("wiosna",3,0, adj=0.23)
mtext("lato",3,0, adj=0.55)
mtext("jesień",3,0, adj=0.85)
|
Wykonanie powyższego zestawu poleceń spowoduje wygenerowanie wykresu:
Funkcja ta ma opcje związane z wypełnianiem wnętrza kreskami nachylonymi pod zadanym kątem i o określonej częstości występowania. Służą do tego opcje density=x i angle=y. Opcja border=”kolor” określa kolor obramowania. Zapis border=NA oznacza rysowanie prostokąta bez obramowania.
W funkcji rect() współrzędne lewego dolnego rogu i współrzędne górnego prawego rogu prostokąta mogą być wektorami równej długości. Umożliwia to wstawienie na wykres kilku jednakowych prostokątów.
Funkcja polygon()
Funkcja polygon() służy do wykreślania dowolnych wielokątów, wypełniania ich zadanym kolorem lub wzorem. Służy przede wszystkim do wykreślania tego, czego nie robią nadrzędne funkcje graficzne. Obowiązkowymi opcjami tej funkcji są: wektor współrzędnych wierzchołków wielokąta odczytanych z osi 0X i wektor współrzędnych wierzchołków wielokata odczytanych z osi 0Y. Oba muszą być równej długości. Współrzędne ostatniego punktu nie muszą pokrywać się ze współrzędnymi pierwszego punktu, gdyż domyślnie zawsze ostatni punkt łączony jest z pierwszym.
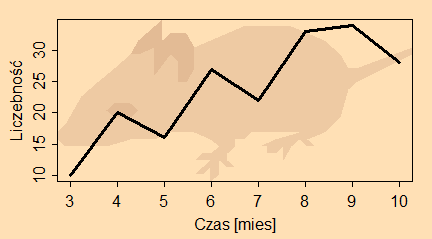
Funkcja polygon(), mimo, że nie kreśli elementów graficznych standardowo umieszczanych na wykresach, jest bardzo często stosowana. Przykładowo za jej pomocą można “narysować” tło wykresu kojarzące zrobione opracowanie z gatunkiem, który był badany. Robi się to często na posterach. Wygląda to następująco:
x=c(0,0,1,6,9,12,14,17,19,20,19,18,17,19,17,18,19,19,20,20,21,22,21,21,
22,22,23,24,30,27,25,26,26,27,28,28,29,30,31,32,31,33,35,36,37,44,44,37,36,
35,33,29,23,17,16,14,13,13,12,10,9,7,5,3,1)
y=c(7,6,5,5,6, 6, 7, 7, 6, 5, 4, 4, 3, 3, 1, 1, 2, 0, 1, 3, 2, 2, 3, 4, 5, 6, 6,
7, 7, 6, 5, 5, 4, 4, 5, 3, 5, 6, 5, 5, 6, 7, 9, 13, 14, 18, 19, 16, 16, 18,
20, 22, 22, 19, 21, 21, 20, 23, 22, 20, 18, 16, 14, 12, 8)
xu=c(12,14,15,15,16,17,17,16,14,12)
yu=c(15,18,17,14,14,16,19,21,21,19)
xu2=c( 9,10,12,13,13,12,10)
yu2=c(18,18,19,20,23,22,20)
xo=c( 6,7,9,10, 9, 7)
yo=c(10,9,9,10,11,11)
windows(4.5, 2.5)
par(mar=c(3,3,1,1), mgp=c(1.7, 0.5, 0), tck=-0.03, bg="#ffe0b5")
plot(3:10, c(10, 20, 16, 27, 22, 33, 34, 28), type="l",lwd=2, xlab="Czas [mies]",
ylab="Liczebność", main="")
wsp.x=(par("usr")[2]-par("usr")[1])/44
wsp.y=(par("usr")[4]-par("usr")[3])/23
polygon(x*wsp.x+par("usr")[1],y*wsp.y+par("usr")[3], col="#eecaa3", border=NA)
polygon(xu*wsp.x+par("usr")[1],yu*wsp.y+par("usr")[3], col="#e3bb95", border=NA)
polygon(xu2*wsp.x+par("usr")[1],yu2*wsp.y+par("usr")[3], col="#e3bb95",
border=NA)
polygon(xo*wsp.x+par("usr")[1],yo*wsp.y+par("usr")[3], col="#e3bb95", border=NA)
lines(3:10, c(10, 20, 16, 27, 22, 33, 34, 28), lwd=3)
box()
|
Wykres uzyskany za pomocą tego programu wygląda następująco:
Znawcy rozpoznają na tym wykresie myszarkę leśną, inni domyślą się, że chodzi o jakąś mysz, a wykres pokazuje jej dynamikę liczebności.
Funkcja podrzedna graficzna utworzona przez użytkownika R
Funkcja polygon() nadaje się do utworzenia takiego wykresu kołowego, jaki tworzy funkcja pie(), ale bez jej ograniczeń (niemożność jej umieszczenia na inaczej podkolorowanym polu kreślenia, niemożliwość nałożenia na wycinki koła kilku kreskowych deseni). Problemy te rozwiązuje poniższa funkcja tworząca wykres kołowy na utworzonym wcześniej wykresie, za pomocą odpowiednio zestawionych “wielokątów” imitujących wycinki kołowe. Wygląda ona następująco:
#Funkcja graficzna podrzędna
#domalowywujaca wykres kołowy w środku wykresu.
pieplot = function(dane, radius=1, init.angle=0,
col=gray(1:length(dane)/length(dane)),
density=rep(NULL, length(dane)),
angle=rep(1:length(dane)*(180/length(dane)))) {
plot.window(c(-1,1), c(-1,1), asp=1)
alpha=dane/sum(dane)*(2*pi)
beta=c(0,cumsum(alpha)[1:(length(dane)-1)])+init.angle
x0=radius*cos(init.angle)
y0=radius*sin(init.angle)
xp=x0
yp=y0
for(i in 1:length(dane)){
j=1
x=c(0,x0)
y=c(0,y0)
while (j*pi/1000<alpha[i]) {
x=c(x, radius*cos(j*pi/1000+beta[i]))
y=c(y, radius*sin(j*pi/1000+beta[i]))
j=j+1}
if (i<length(dane)) {x0=radius*cos(beta[i+1])
y0=radius*sin(beta[i+1])}
if (i==length(dane)) {x0=xp
y0=yp}
x=c(x,x0)
y=c(y,y0)
polygon(x,y, col=col[i], density=density[i], angle=angle[i])}}
|
Funkcja ta nie ma wszystkich opcji graficznych, jakie zazwyczaj mają funkcje graficzne w R, ale osoby trochę już programujące z łatwością mogą zmodyfikować jej kod. Jej użycie wygląda następująco:
windows(4.5, 2.5)
par(mar=c(1.5,1.5,1.5,6), mgp=c(0.2,0,0), bg="#ffcccc")
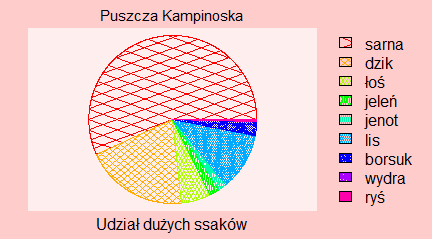
plot(1:10, type="n", axes=FALSE, xlab="Udział dużych ssaków", ylab="",
main="Puszcza Kampinoska", cex.main=0.9, font.main=1)
grid(100,50,lty=1,lwd=10,col="#ffeeee")
pieplot(c(2000,700,200,70,54,390,95,3,12), col=rainbow(9), density=1:9*10,
angle=1:9*180/9)
pieplot(c(2000,700,200,70,54,390,95,3,12), col=rainbow(9), density=1:9*10,
angle=-(1:9*180/9))
par(xpd=TRUE)
legend(par("usr")[2]+0.1,sum(par("usr")[3:4])/2, bty="n", fill=rainbow(9),
density=1:9*10, angle=1:9*180/9, xjust=0, yjust=0.5,
legend=c("sarna","dzik", "łoś", "jeleń", "jenot", "lis", "borsuk", "wydra",
"ryś"))
legend(par("usr")[2]+0.1,sum(par("usr")[3:4])/2, bty="n", fill=rainbow(9),
density=1:9*10, angle=-(1:9*180/9), xjust=0, yjust=0.5,
legend=c("","", "", "", "", "", "", "", ""))
|
Powstanie w ten sposób następujący wykres: