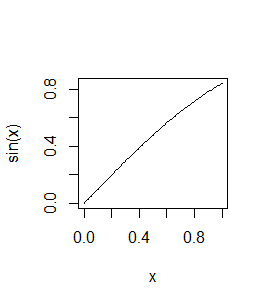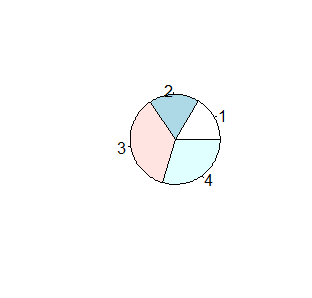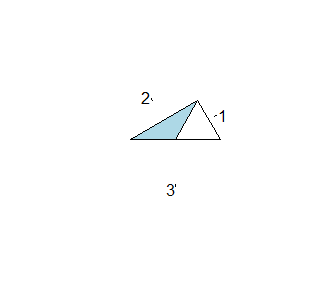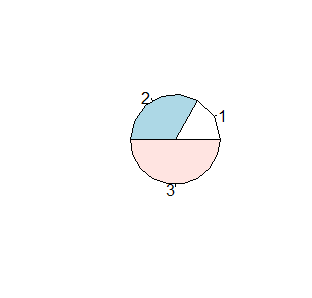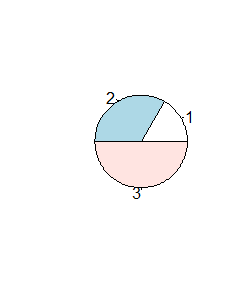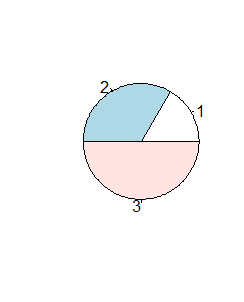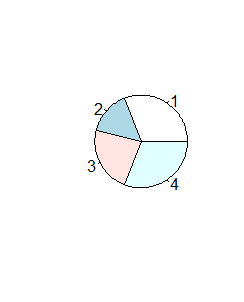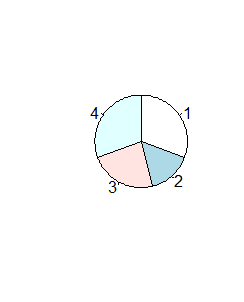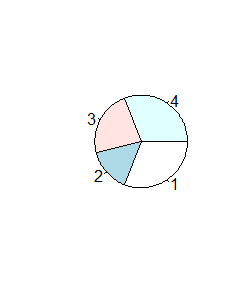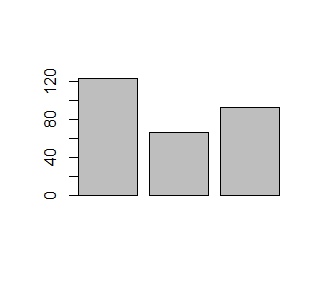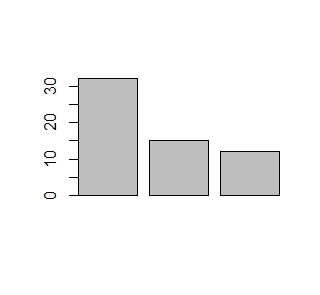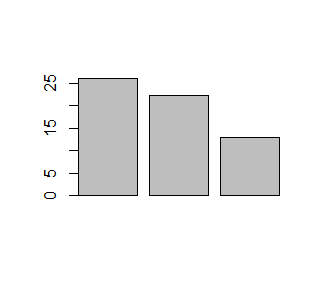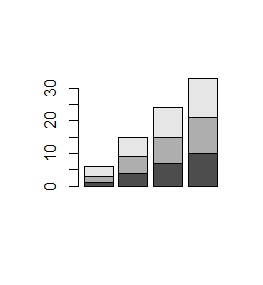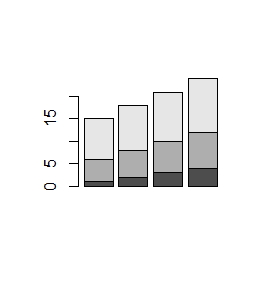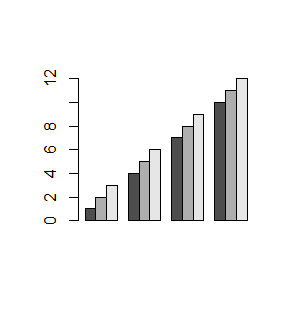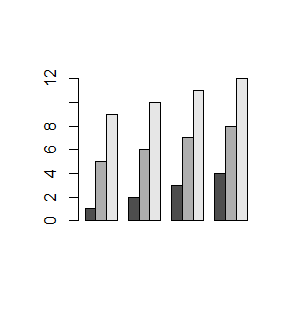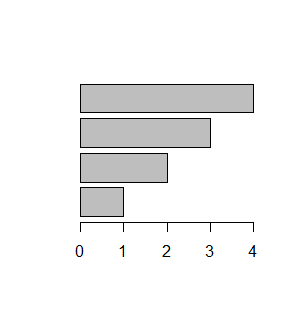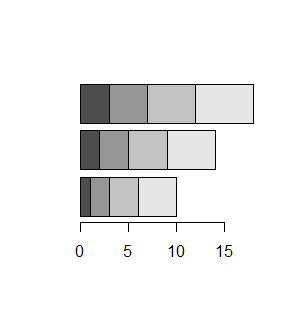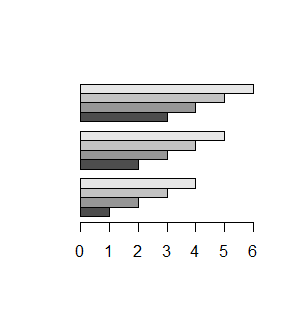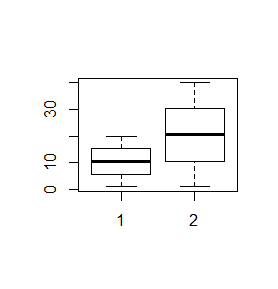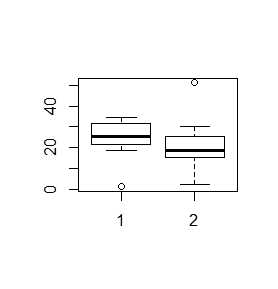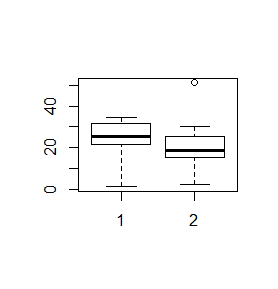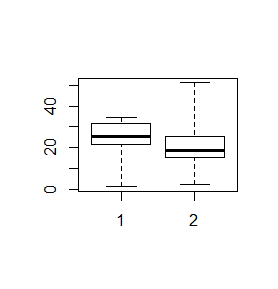Wybrane nadrzędne funkcje graficzne
Funkcja plot()
Funkcja plot() służy do zobrazowania danych zapisanych w wektorach, macierzach, szeregach czasowych i bardziej skomplikowanych strukturach, których elementami są wektory. W najprostszej wersji, gdy zastosujemy ją na pojedynczym wektorze x pojawi się wykres pokazujący rozrzut punktów o współrzędnych (i, x[i]).
> x=c(850, 950, 700, 550, 900, 650, 650, 800, 30, 700) > plot(x) |
Polecenie to powoduje pojawienie się okna graficznego a w nim wykresu rozrzutu punktów o współrzędnych (i, x[i]).
Okno graficzne w R ma swój numer (od 2 w górę) i oznaczenie czy jest aktywne czy nie (ACTIVE/INACTIVE). Można go rozszerzyć na cały ekran lub ściągnąć do paska zadań. Jego wielkość można regulować myszą, z tym, że zbyt małe rozmiary spowodują wygenerowanie komunikatu figure margines to large.
Wykres znajdujący się w oknie graficznym można metodą Ctrl+C, Ctrl+V skopiować do dowolnego pliku graficznego. Można go też zapamiętać w jednym z formatów: Metafile, Postscript, PDF, Png, Bmp, TIFF, Jpeg. Zapisuje się w ten sposób sam wykres bez niebieskich obramowań okna graficznego w R.
Wykresy typu plot() inaczej działają, gdy wprowadzi się do nich ciąg liczbowy a inaczej, gdy działają na obiekcie typu factor.
> x=c(1, 8, 2, 1, 1, 8, 8, 8, 2, 2, 1, 1, 8, 8, 2, 8, 1) > plot(x) > plot(factor(x)) |
Jeden po drugim powstają następujące wykresy:
Jeszcze inny typ wykresu powstanie gdy argumentami funkcji plot() są dwa wektory, czynnik i wektor oraz dwa czynniki.
> y=c(850, 950, 700, 550, 900, 650, 650, 800, 650, 700, 600, 850, 900, 750) > x=c(1, 3, 2, 1, 1, 3, 3, 3, 2, 2, 1, 1, 3, 3) > plot(x,y) > plot(factor(x),y) > plot(factor(x),factor(y)) |
Powstaną kolejno następujące wykresy:
Funkcja plot() służy także do tworzenia wykresów liniowych, punktowo-liniowych, schodkowych, kreskowych za pomocą opcji type=. Wartościami tej opcji są symbole literowe napisane w cudzysłowie.
> x=c(4.84, 1.12, 3.57, 10.57, 0.12, 2.55, 3.10, 3.18, 1.93, 4.15, 7.11, 8.22, 9.96, 0.50, 7.62, 4.33, 7.03, 1.28, 8.42, 1.96) > plot(x,type="p") > plot(x,type="l") > plot(x,type="b") > plot(x,type="c") > plot(x,type="o") > plot(x,type="h") > plot(x,type="s") > plot(x,type="S") > plot(x,type="n") |
Po kolei powstaną wykresy:
Ostatni typ wykresu przydaje się, gdy chcemy na układ współrzędnych o ustalonym zakresie nałożyć nietypowy rysunek.
Przy rysowaniu wykresu rozrzutu punktów (x[i],y[i]) można zastosować skalę logarytmiczną o podstawie 10.
> x=c(4.84, 1.12, 3.57, 10.57, 0.12, 2.55, 30.10, 30.18, 100.93, 400.15) > y=c(0.77, 0.13, 0.71, 0.51, 0.04, 0.82, 1.70, 2.80, 10.37, 10.67) > plot(x, y) > plot(x, y, log="x") > plot(x, y, log="y") > plot(x, y, log="xy") |
Powstaną kolejno następujące wykresy:
Funkcja matplot()
Nierzadko w biologii wykonuje się pomiary zmiennej Y przy określonych z góry wartościach zmiennej X. Jeżeli tego typu eksperyment powtarza się w kilku wariantach (ale dla takich samych wartości zmiennej X) to uzyskane wyniki można zapisać w macierzy. Zobrazowanie tych wyników w postaci punktów o różnych kolorach lub znacznikach, albo różnych linii najwygodniej wykonać za pomocą funkcji matplot().
> temp=c(10, 15, 20, 25, 30) > y1=c(0.77, 1.13, 1.71, 2.51, 3.04) > y2=c(0.22, 0.23, 0.65, 1.32, 2.11) > y3=c(0.41, 0.95, 1.32, 2.03, 2.86) > y=cbind(y1,y2,y3) > matplot(temp, y) > matplot(temp, y, pch=20) > matplot(temp, y, type="l") |
Powyższe polecenia spowodowały powstanie po kolei dwóch wykresów:
Standardowo funkcja matplot() w miejsce wartości stawia numer kolumny, z której pochodzą dane. Opcja pch= o wartościach od 1 do 20 w miejsce to stawia znacznik o określonym kształcie. Opcja type= może mieć wartości “p”,”l”,”b”,”c”, “o”, “h”, “s”, “S”, “n” i zmienia typ wykresu tak samo jak w funkcji plot().
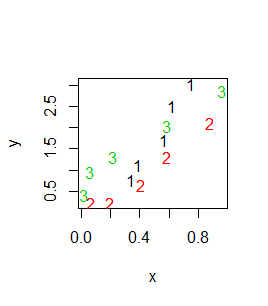
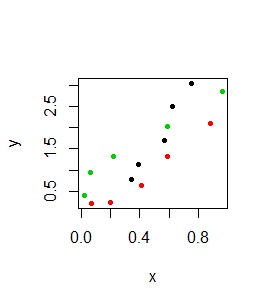
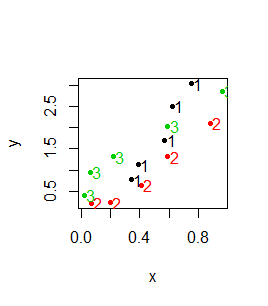
Jeżeli mierzymy dla tych samych obiektów dwie zmienne X i Y (np. długość i masę) a obiekty pochodzą z trzech populacji statystycznych wartości zmiennej X możemy zapisać w jednej macierzy, a zmiennej Y w drugiej. Wtedy funkcja matplot() odpowiednio przyporządkowuje dane do siebie.
> x x1 x2 x3 [1,] 0.34 0.07 0.02 [2,] 0.39 0.20 0.06 [3,] 0.57 0.41 0.22 [4,] 0.62 0.59 0.59 [5,] 0.75 0.88 0.96 > y y1 y2 y3 [1,] 0.77 0.22 0.41 [2,] 1.13 0.23 0.95 [3,] 1.71 0.65 1.32 [4,] 2.51 1.32 2.03 [5,] 3.04 2.11 2.86 > matplot(x, y) > matplot(x, y, pch=20) > matplot(x, y, type="l") |
Powyższe polecenia spowodują powstanie po kolei następujących wykresów:
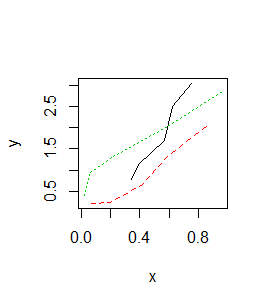
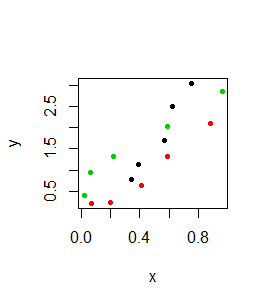
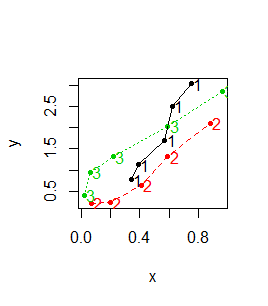
Z funkcją graficzną matplot() współdziałają funkcje graficzne dokładające matpoints() oraz matlines(). Pierwsza z nich dokłada do wykresu numer kolumny, z której pochodzą dane, druga dokłada linie do wykresu, w którym występują liczby.
> x x1 x2 x3 [1,] 0.34 0.07 0.02 [2,] 0.39 0.20 0.06 [3,] 0.57 0.41 0.22 [4,] 0.62 0.59 0.59 [5,] 0.75 0.88 0.96 > y y1 y2 y3 [1,] 0.77 0.22 0.41 [2,] 1.13 0.23 0.95 [3,] 1.71 0.65 1.32 [4,] 2.51 1.32 2.03 [5,] 3.04 2.11 2.86 > matplot(x, y, pch=20) > matpoints(x+0.05,y) > matlines(x,y) |
Pierwszy z pokazanych wykresów przechodzi na drugi, a drugi na trzeci:
Funkcja matplot() działa na odpowiadających sobie wektorach lub macierzach. Działa także gdy odpowiadające sobie wektory są zapisane w typie data.frame, choć z formalnego punktu widzenia nie są to bazy danych (baza danych miałaby jedna kolumnę będącą czynnikiem, która pokazywałaby do jakiej kategorii należą dane i tylko jedną kolumnę na wartości zmiennej X i jedna kolumnę na wartości zmiennej Y).
Funkcja curve()
Funkcje plot() i matplot() z opcją type=”l” umożliwiły robienie wykresów liniowych. Wykresy liniowe stosuje się do obrazowania wszelkich funkcji matematycznych jednej zmiennej. Zastosowanie wymienionych funkcji graficznych wymagałoby wyliczenie najpierw wektora wartości x dla jakich wyliczone będą wartości funkcji f(x) zapisane w drugim wektorze y, a następnie wykonanie funkcji plot(x,y,type=”l”). Działania te skraca funkcja graficzna curve() o specjalnej składni:
curve(nazwa_funkcji, from=x_min, to=x_max)
Domyślnie x_min=0 i x_max=1.
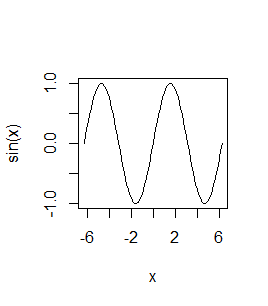
> curve(sin) > curve(sin,-2*pi,2*pi) |
Po kolei powstaną dwa wykresy:
Takie same wykresy powstaną gdy zastosujemy składnię curve(sin(x)) oraz curve(sin(x),-2*pi, 2*pi). Składnię ze wskazaniem argumentu należy stosować gdy w miejscu funkcji zastosuje się działania matematyczne (np. 10*sin(x)). Ponadto funkcja ta ma opcję logiczną add= mającą standardowo wartość FALSE. Kiedy zmienimy ją na TRUE powstanie funkcja graficzna dokładająca. Umożliwia to narysowanie kilku funkcji matematycznych na jednym wykresie.
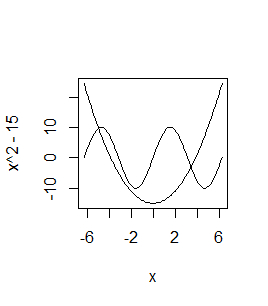
> curve(x^2-15,-2*pi,2*pi) > curve(10*sin(x),add=TRUE) |
Spowoduje to powstanie następującego wykresu:
Funkcja pie()
Jeżeli w jednym zgrupowaniu zakwalifikujemy obiekty do kilku kategorii zwyczajowo podaje się procent obiektów należących do pierwszej, drugiej, n-tej kategorii. Jednym z najpopularniejszym sposobem obrazowania wyników takich badań jest podział koła na części o powierzchni proporcjonalnej do procentu obiektów należących do danej kategorii. W R służy do tego funkcja pie(). Jest to funkcja, która odpowiedni procent sama wylicza dla dowolnego ciągu.
> N=c(10,11,22,18) > proc=N/sum(N)*100 > pie(N) > pie(proc) |
Kolejno pojawiające się wykresy są identyczne.
Funkcja pie() nie działa na czynnikach, natomiast na szeregach czasowych działa tak samo, jak na wektorach, z których ten szereg został utworzony.
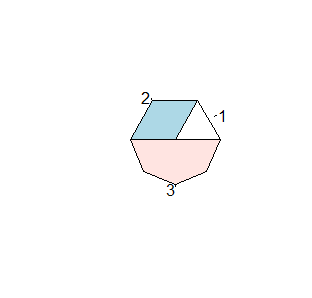
Niektóre opcje funkcji pie() zmieniają istotnie kształt wykresu. Może być to wielokąt z dodanymi punktami wyznaczonymi przez końce odcinków wychodzących z jednego punktu i kątach między nimi proporcjonalnych do wartości wyrazów wektora. Ustala się to za pomocą opcji edge=x, gdzie x ma domyślną wartość 200.
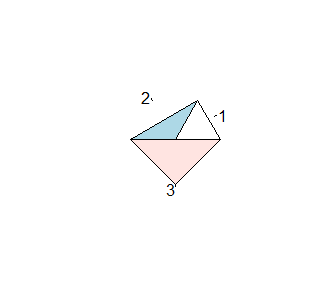
| > x=c(1,2,3) > pie(x, edge=1) > pie(x, edge=6) > pie(x, edge=10) > pie(x, edge=20) |
Powstałe w ten sposób figury nie specjalnie nadają się do obrazowania wyników badań.
Wykres kołowy wydaje się bardzo niewielki na tle całego wykresu a odpowiada za to domyślna opcja radius=x mająca wartość 0.8. Ustawienie jej na 1 całkowicie wypełnia pole kreślenia, a większa wartość powoduje, że figura nie mieści się w polu kreślenia.
> x=c(1,2,3) > pie(x) > pie(x, radius=1) > pie(x, radius=1.5) |
Powstaną w ten sposób kolejno trzy wykresy:
Opcja logiczna clockwise określa kierunek, w jakim przyporządkowywane są wycinkom koła odpowiednie wartości. Standardowo jest to kierunek przeciwny do ruchu wskazówek zegara i można to zmienić wpisując clockwise=TRUE. Z kolei opcja init.angle=x określa kąt nachylenia promienia, od którego rozpoczyna się wykres, do osi 0X. Kąt ten wyrażany jest w stopniach.
> x=c(4,2,3,4) > pie(x) > pie(x, clockwise=TRUE) > pie(x, clockwise=TRUE, init.angle=0) |
Spowoduje to powstanie kolejno trzech wykresów.
Funkcja ta nie ma więcej możliwości graficznych, np wysuwania nieco wyróżnionego odcinka koła, patrzenia na wykres kołowy pod kątem (zmienia się on wtedy w elipsę). Tego typu możliwości (bardziej potrzebne do wizualizacji danych na posterach lub prezentacjach, niż w pracy naukowej) można uzyskać dopiero w dodatkowych pakietach graficznych.
Funkcja barplot()
Liczbę lub procent wyróżnionych obiektów w różnych zgrupowaniach zazwyczaj pokazuje się na wykresach słupkowych. Gdy dysponujemy tego typu danymi, możemy wykonać wykres słupkowy używając funkcji barplot()
> N=c(123, 67, 93) > A=c(32, 15,12) > proc=A/N*100 > barplot(N) > barplot(A) > barplot(proc) |
Kolejno powstaną następujące wykresy:
Dla wektora liczbowego funkcja barplot() tworzy szereg słupków o wysokości określonej przez podane liczby. Ich interpretacja zależy od sposobu przygotowania danych.
Funkcja barplot() działa także na macierzach liczbowych. Tworzy wtedy słupki o wysokości równej sumie liczb w poszczególnych kolumnach, których części o długości równej poszczególnym liczbom w kolumnach są inaczej zaciemnione.
> mat=matrix(1:12,3,4) > mat [,1] [,2] [,3] [,4] [1,] 1 4 7 10 [2,] 2 5 8 11 [3,] 3 6 9 12 > barplot(mat) > mat1=matrix(1:12,3,4,byrow=TRUE) > mat1 [,1] [,2] [,3] [,4] [1,] 1 2 3 4 [2,] 5 6 7 8 [3,] 9 10 11 12 > barplot(mat1) |
Kolejno powstaną dwa wykresy:
Opcja logiczna beside=TRUE powoduje, że części słupków związane z daną liczbą w macierzy są zestawiane obok siebie.
> mat=matrix(1:12,3,4) > mat > barplot(mat, beside=TRUE) > mat1=matrix(1:12,3,4,byrow=TRUE) > barplot(mat1,beside=TRUE) |
Wykresy, które teraz powstaną wyglądają następująco:
Funkcja barplot() umożliwia także robienie wykresów słupkowych ułożonych poziomo. Służy do tego opcja logiczna horiz=, która standardowo ma wartość domyślna FALSE. Po zmianie jej wartości na TRUE powstanie wykres o orientacji poziomej.
> x=1:4 > barplot(x,horiz=TRUE) > xx=cbind(1:4,2:5,3:6) > barplot(xx,horiz=TRUE) > barplot(xx,horiz=TRUE,beside=TRUE) |
Spowoduje to powstanie następujących wykresów:
Argumentem funkcji barplot nie może być czynnik ani szereg czasowy.
Funkcja boxplot()
W Excelu, z braku możliwości zrobienia wykresu pudełkowego, średnie lub mediany wartości jakiejś zmiennej ciągłej wyliczonej w kilku zgrupowaniach wraz z odchyleniami standardowymi, odchyleniami ćwiartkowymi rysuje się na wykresach słupkowych. Wykres pudełkowy znacznie lepiej oddaje ideę średniej, która nie musi zaczynać się od 0 i może mieć wartości ujemne (np. dla temperatury w °C). W R wykresy tego typu tworzy się za pomocą funkcji boxplot(). W przeciwieństwie do funkcji barplot() jest to funkcja nie tylko rysująca wykres, ale przeliczająca dane.
> x=1:20 > y=1:40 > boxplot(x,y) |
Spowoduje to powstanie wykresu wyglądającego następująco:
Centralną część pudełka zajmuje mediana ciągu, dolny koniec pudełka to pierwszy kwartyl, górny koniec to trzeci kwartyl, dolny koniec centralnej kreski to wartość minimalna wektora, a jej górny koniec to wartość maksymalna. Wszystkie te wielkości wyliczono osobno dla pierwszego i drugiego wektora i, co więcej, wektory te nie muszą być jednakowej długości.
Rzeczywiste dane rzadko kiedy mają regularnie zmieniające się wartości. Często pojawiają się wartości odbiegające od pozostałych. Funkcja boxplot() ocenia czy dane mieszczą się w obszarze wyznaczonym przez iloczyn odległości międzykwartylowej oraz liczbę określoną przez opcję range=x. Opcja ta ma domyślną wartość 1.5. Odbiegające dane, nie mieszczące się w wyznaczonym obszarze, są umieszczane jako osobne kółeczka, a ekstrema, zaznaczone jako końce centralnej kreski, są wyznaczane dla pozostałych danych.
> x=c(0.03, 31.49, 18.49, 22.23, 32.96, 26.48, 31.58, 21.26, 24.64, 34.69) > y=c(29.97, 20.35, 18.44, 51.17, 2.00, 15.33, 15.36) > boxplot(x,y) > boxplot(x,y,range=2) > boxplot(x,y,range=3) |
Daje to następujące wykresy.
Nadanie opcji range= wartości 0 powoduje, że wszystkie dane są uwzględniane przy wyliczaniu końców centralnej kreski.
Opcja width=c(n1,n2,..,nk) określa względne szerokości kolejnych pudełek. Jej odmiana, opcja logiczna varwidth=TRUE powoduje, że szerokości pudełek będą proporcjonalne do wielkości prób, z których wyliczana jest mediana.
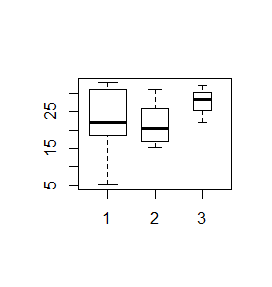
> x=c(5.03, 31.49, 18.49, 12.23, 32.96, 26.48, 31.58, 21.26, 24.64, 14.69, 21.3, 22.8, 31.2, 19.7) > y=c(29.97, 20.35, 18.44, 51.17, 22.00, 15.33, 15.36) > z=c(22.1, 32.3, 28.5) > boxplot(x,y,z) > boxplot(x,y,width=c(3,2,1)) > boxplot(x,y,varwidth=TRUE) |
Spowoduje to wygenerowanie kolejno trzech wykresów.
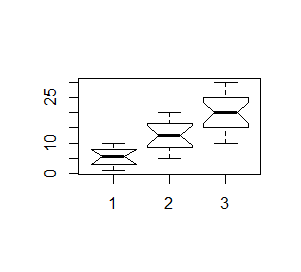
Analizy statystyczne dla porównania median spowodowały, że zaczęto rysować pudełka wcięte. Wcięcia są obliczane za pomocą specjalnej procedury statystycznej wyjaśnionej w podręczniku John M. Chambers, William S. Cleveland, Paul A. Tukey, Beat Kleiner (1983) Graphical Methods for Data Analysis. Duxbury Press, na stronie 62. Wynika z nich, że jeżeli wcięcia dwóch pudełek nie zachodzą na siebie to mediany dwóch rozkładów istotnie różnią się od siebie. Wyjaśnienie tej terminologii będzie miało miejsce na statystyce, natomiast by uzyskać pudełka wcięte w R wystarczy do funkcji boxplot() dodać opcję logiczną notch=TRUE.
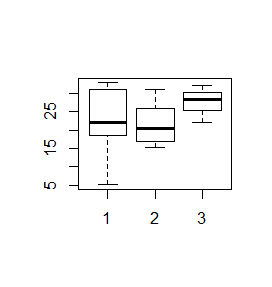
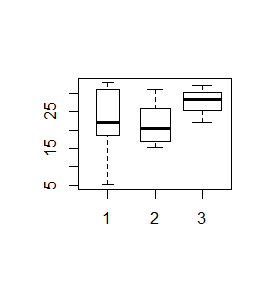
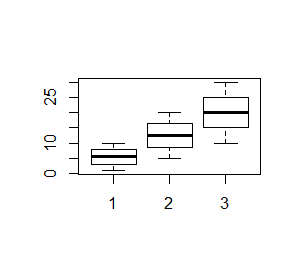
> x=1:10 > y=5:20 > z=10:30 > boxplot(x,y,z) > boxplot(x,y,z, notch=TRUE) |
Powstaną kolejno dwa wykresy:
Składnię funkcji boxplot() dostosowano także do tego, by działała na bazach danych. Wtedy istnieje kolumna z danymi i kolumna pokazująca, do której kategorii należą dane. Należy wtedy zastosować składnię:
boxplot(nazwa_zmiennej ~ nazwa_czynnika, nazwa_bazy) Przykładowo dla bazy iris zaimplementowanej do R, zmienną, której mediany liczymy, może być Sepal.Length, a czynnikiem Species. Można napisać polecenie:
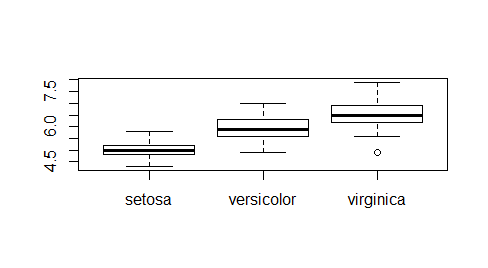
> boxplot(Speal.Length ~ Species, iris) |
i uzyskać następujący wykres:
Wszystkie pokazane wykresy można uzyskać w postaci poziomej stosując opcję horiz=TRUE
Funkcja boxplot() poza tym, że rysuje wykres, tworzy także listę obiektów z danymi, które można ewentualnie wykorzystać do innych celów. Aby zobaczyć tę listę należy funkcję tę przyporządkować jakiemuś literałowi, a następnie wywołać ją poprzez literał.
> ir = boxplot(Speal.Length ~ Species, iris) > ir $stats [,1] [,2] [,3] [1,] 4.3 4.9 5.6 [2,] 4.8 5.6 6.2 [3,] 5.0 5.9 6.5 [4,] 5.2 6.3 6.9 [5,] 5.8 7.0 7.9 # $n [1] 50 50 50 # $conf [,1] [,2] [,3] [1,] 4.910622 5.743588 6.343588 [2,] 5.089378 6.056412 6.656412 # $out [1] 4.9 # $group [1] 3 # $names [1] "setosa" "versicolor" "virginica" |
Macierz będąca pierwszym elementem tej listy to podstawowe charakterystyki statystyczne służące do utworzenia pudełek (ekstrema, kwartyle i mediany). Druga macierz będąca elementem listy o nazwie conf to początki i końce ewentualnych wcięć w pudełkach, które można wywołać opcją notch=TRUE.
Funkcja hist()
Histogramy są graficznym obrazem tego, co w statystyce nazywane jest rozkładem z próby (ang. sample distribution). Możemy go utworzyć za pomocą funkcji hist(). Jej przydatność wynika stąd, że sama wykonuje wszelkie obliczenia pozwalające na utworzenie takiego wykresu.
> x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69, 29.73, 22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70, 12.00, 23.35, 2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90) > hist(x) |
Polecenie to powoduje uaktywnienie się okienka graficznego, w którym został automatycznie stworzony wykres słupkowy.
Wysokość słupków pokazuje jakie jest zagęszczenie liczb w przetwarzanym ciągu w przedziale będącym podstawą słupka. Aby wszystko było jasne przedstawiam nomenklaturę stosowaną przy opracowaniu danych. Jeżeli N jest liczbą wszystkich danych, a N(x1,x2] liczbą danych należących do przedziału (x1,x2] to:
N(x1,x2] jest liczebnością,
N(x1,x2]/N jest frakcją albo prawdopodobieństwem,
N(x1,x2]/N*100 jest procentem,
N(x1,x2]/(x2-x1) jest zagęszczeniem,
N(x1,x2]/(N*(x2-x1)) jest intensywnością (gęstością) prawdopodobieństwa.
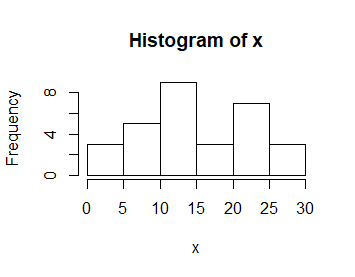
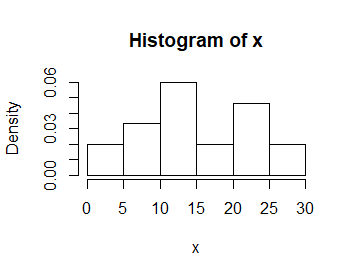
Funkcja hist() tworzy standardowo wykresy liczebności danych i suma wysokości wykreślonych słupków jest równa liczbie wszystkich obiektów. Natomiast najlepszą interpretację w odniesieniu do rzeczywistości mają wykresy intensywności prawdopodobieństwa. Są one przybliżeniem prawdopodobieństwa z jakim możemy wylosować obiekt o danej wartości zmiennej z całej populacji. Wykres intensywności prawdopodobieństwa uzyskamy stosując jedną z opcji: freq=FALSE albo prob=TRUE.
> x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69, 29.73, 22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70, 12.00, 23.35, 2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90) > hist(x, prob=TRUE) |
Powstały wykres różni się od poprzedniego tylko liczbami na osi pionowej.
W tego typu wykresie suma pół powierzchni wykreślonych słupków jest równa 1.
Liczba i długość przedziałów, w których zliczane są dane, jest wyznaczana domyślnie. Nazywa się je przedziałami histogramowania. Domyślnie są to przedziały prawostronnie domknięte, a lewostronnie otwarte (poza pierwszym przedziałem, który jest obustronnie domknięty). Ich granice trzeba ustalić arbitralnie i zazwyczaj robi się to tak, by były to jakieś “okrągłe” liczby. Opcja breaks=c(n1,n2,…,nk) pozwala na sztywne określenie tych granic.
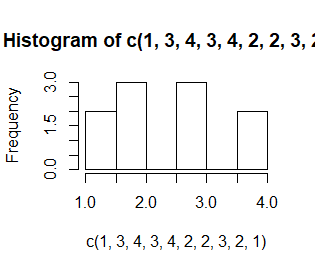
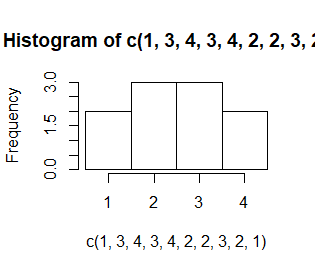
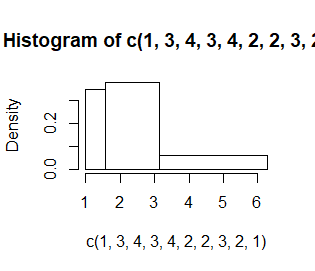
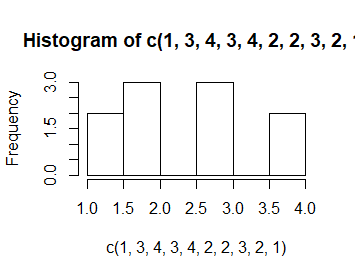
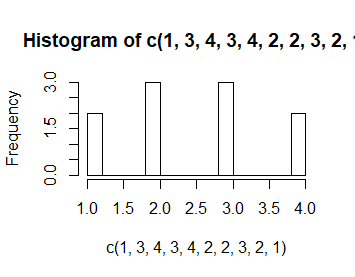
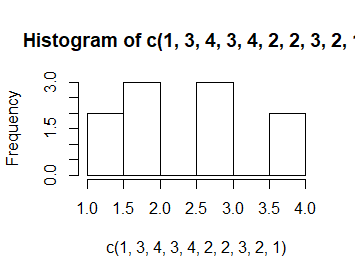
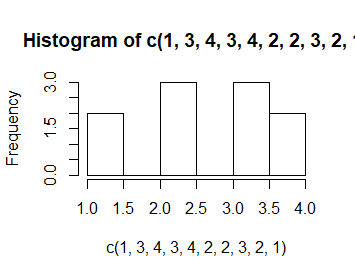
> hist(c(1,3,4,3,4,2,2,3,2,1)) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=c(0.5,1.5,2.5,3.5,4.5)) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=c(pi/2, pi, 2*pi)) |
Kolejno powstają zupełnie niepodobne do siebie wykresy mimo, ze dotyczą tych samych danych. Dodatkowo, przy nierównych przedziałach uruchomiła się automatycznie opcja prob=TRUE.
Ta sama opcja, breaks, ale o wartości będącej liczba całkowitą, breaks=n pozwala do pewnego stopnia zmienić liczbę przedziałów histogramowania. Przeszkadza jej w tym tylko algorytm wyznaczania granic tych przedziałów jako ładnych “okrągłych” liczb, co powoduje, że nie działa ona dokładnie.
> hist(c(1,3,4,3,4,2,2,3,2,1), breaks=2) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=3) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=4) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=5) > hist(c(1,3,4,3,4,2,2,3,2,1),breaks=11) |
Opcja right=FALSE umożliwia stosowanie przedziałów histogramowania lewostronnie domkniętych a prawostronnie otwartych.
> hist(c(1,3,4,3,4,2,2,3,2,1)) > hist(c(1,3,4,3,4,2,2,3,2,1),right=FALSE) |
Nawet taka mała różnica powoduje zmianę wykresu.
Wszystko to pokazuje, jak wielkie znaczenie ma sposób podziału osi 0X na przedziały histogramowania.
Warto wiedzieć, że wielkości potrzebne do zrobienia histogramu także zapisywane są w liście, którą można zobaczyć, a nawet wykorzystać w różnych operacjach. Gdy zapisze się wykres jako obiekt o danej nazwie, wystarczy popatrzyć co kryje się pod tą nazwą:
> x=c(18.03, 11.49, 18.49, 22.23, 12.96, 6.48, 11.58, 21.26, 24.64, 4.69, 29.73, 22.11, 2.00, 5.29, 23.60, 13.53, 27.66, 21.26, 11.66, 5.10, 11.70, 12.00, 23.35, 2.45, 16.12, 11.00, 11.96, 28.69, 7.11, 6.90) > hist(x)->a > a $breaks [1] 0 5 10 15 20 25 30 # $counts [1] 3 5 9 3 7 3 # $density [1] 0.02000000 0.03333333 0.06000000 0.02000000 0.04666667 0.02000000 # $mids [1] 2.5 7.5 12.5 17.5 22.5 27.5 # $xname [1] "x" # $equidist [1] TRUE # attr(,"class") [1] "histogram" |
Powstaje lista złożona z “breaks” – granic przedziałów histogramowania, “counts” – liczby wartości ciągu w kolejnych przedziałach histogramowania, “density” – intensywności prawdopodobieństwa, “mids” – środkach przedziałów histogramowania i domyślnych wartości podstawowych opcji. Do pokazanych wartości mamy dostęp i możemy ich użyć w innych wykresach. Przykładowo by utworzyć rozkład procentowy, wystarczy zastosować funkcję barplot() do danych a[[2]]/length(x)*100. Można wręcz napisać polecenie barplot(hist(x)[[2]]/length(x)*100)
Podstawowe opcje nadrzędnych funkcji graficznych
Funkcje graficzne posiadają szereg opcji, które wpisuje się wewnątrz nawiasów okrągłych na zasadzie opcja=… i oddziela przecinkami. Wiele z nich jest jednakowych dla wszystkich przedstawionych funkcji. Umożliwiają zatytułowanie wykresu, podpisanie osi, określenie kolorów i wzorów różnych elementów wykresu i wiele innych rzeczy. Najbardziej potrzebne na ten moment wydają się opcje związane z utworzeniem tytułu wykresu i podpisów pod osiami, bo to co proponują opcje domyślne funkcji graficznych rysujących jest nie do przyjęcia. Opcje te wyglądają następująco:
- main=”” Tytuł wykresu napisany na górnym marginesie.
- sub=”” Podpis wykresu napisany na dolnym marginesie.
- xlab=”” Tytuł osi 0X napisany na dolnym marginesie.
- ylab=”” Tytuł osi 0Y napisany na lewym marginesie.
Ich zastosowanie pokazują następujące programy:
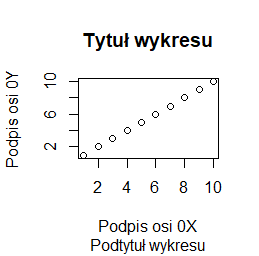
plot(1:10, main="Tytuł wykresu", sub="Podpis wykresu", xlab="Podpis osi 0X", ylab="Podpis osi 0Y") |
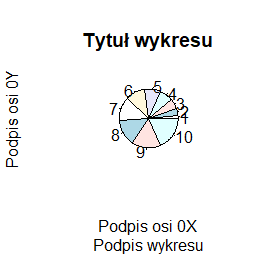
pie(1:10, main="Tytuł wykresu", sub="Podpis wykresu", xlab="Podpis osi 0X", ylab="Podpis osi 0Y") |
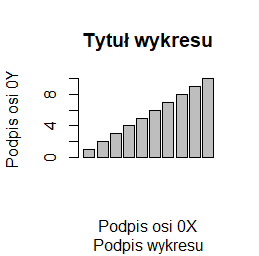
barplot(1:10, main="Tytuł wykresu", sub="Podpis wykresu", xlab="Podpis osi 0X", ylab="Podpis osi 0Y") |
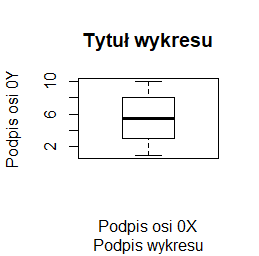
boxplot(1:10, main="Tytuł wykresu", sub="Podpis wykresu", xlab="Podpis osi 0X", ylab="Podpis osi 0Y") |
Programy te trzeba wykonywać po kolei, by uzyskać cztery następujące wykresy:
Inne opcje modyfikujące wykresy opisywane będą przy okazji opisywania różnych problemów związanych z wykonaniem wykresu. Tu pokazujemy wykaz najczęściej stosowanych:
- adj= Sposób wyśrodkowania napisów i podpisów. 0 (z lewej), 0.5 (wyśrodkowane), 1 (do prawej). Może być dowolną liczbą z przedziału [0,1].
- col.main= Kolor tytułu.
- col.sub= Kolor podpisu.
- col.lab= Kolor podpisów osi.
- col= Kolor elementów wykresu.
- ps= Wielkość czcionki.
- xlim=c(a,b) Zakres zmienności danych na osi 0X (od liczby a do liczby b).
- ylim=c(a,b) Zakres zmienności danych na osi 0Y (od liczby a do liczby b).
- pch= Wzór znaczników dla punktów.
- cex= Wielkość znaczników.
- lty= Typ linii w wykresach liniowych, punktowo liniowych i schodkowych.
- lwd= Grubość linii w wykresach liniowych, punktowo liniowych i schodkowych.
- asp=x Jednostki na osi 0Y w stosunku do jednostek na osi 0X są równe x (dotyczy funkcji plot( ), matplot(), barplot() i curve()).
Nie wyczerpuje to wszystkich opcji stosowanych w funkcjach graficznych. Ich wykaz można zobaczyć po wpisaniu w R polecenia ?Nazwa_funkcji. Pokazuje się strona internetowa z obszernego, oficjalnego podręcznika do programu R. Każda z tych stron ma ujednolicony schemat:
Nazwa biblioteki |
Nazwa funkcji |
Usage Formalna bodowa funkcji Alternatywna formalna budowa funkcji ... |
Arguments Wykaz obowiązkowych argumentów i ich typ Wykaz dodatkowych argumentów (parametrów) i ich wartości domyślne |
Details Uwagi dotyczące poszczególnych opcji, ich wartości, związku z innymi funkcjami |
References Literatura opisująca dany rodzaj wykresu, sposób jego zaprogramowania itp. |
See also Linki do powiązanych funkcji |
Examples Przykłady programów |
Formalna budowa funkcji pokazuje formalne nazwy poszczególnych argumentów. Jeżeli pierwszym argumentem jest x, a części “Arguments” znajdujemy informację, że x jest wektorem numerycznym to możemy:
1. Po nazwie funkcji i otworzeniu nawiasu wstawić nazwę wektora numerycznego na pierwszym miejscu.
2. Po nazwie funkcji i otworzeniu nawiasu wstawić x=”nazwa wektora numerycznego” nie koniecznie na pierwszym miejscu.
Podobna zasada dotyczy w R każdej zdefiniowanej funkcji. Przy pisaniu funkcji bez nazw parametrów nalezy stosować taką kolejność wstawiania ich wartości, jaka występuje w formalnej definicji funkcji.
Niekiedy dzięki opcjom nadrzędnych funkcji graficznych powstaje wystarczająco dobry wykres. Jednocześnie wiele elementów uzyskanych dzięki tym opcjom (widok osi, znaczników, podpisy) można nałożyć na wykres poprzez funkcje graficzne podrzędne. Powoduje to, że dalszą część podręcznika skonstruowano na zasadzie wykazu różnych problemów związanych z zaprogramowaniem dobrego wykresu, nie opisów funkcji i ich opcji, jak to zrobiono w tym rozdziale. Niekiedy też informacje powtarzają się, ale w ten sposób łatwiej je znaleźć.