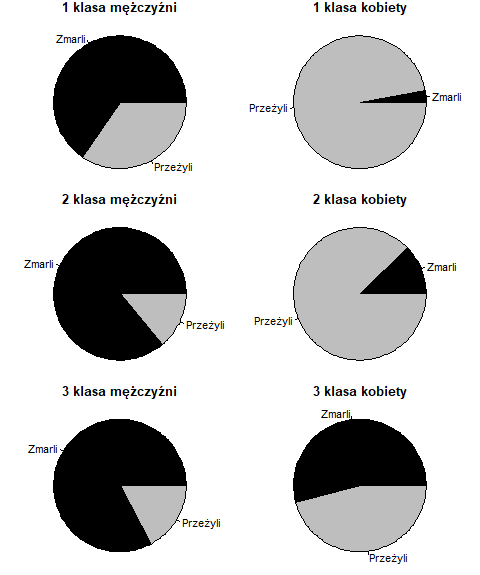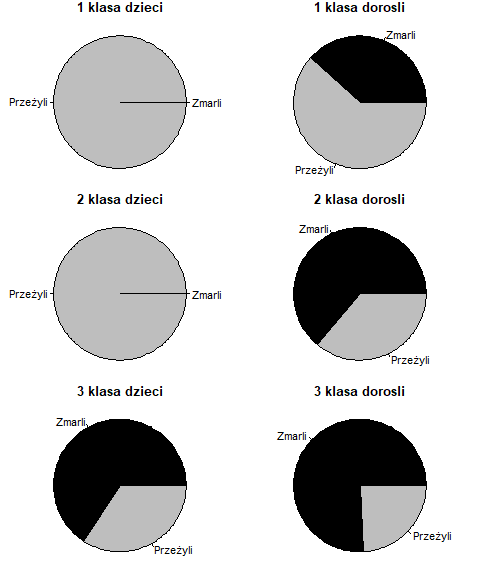Wykresy kołowe, zastosowanie
Uwagi ogólne
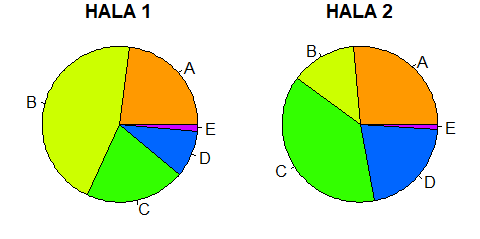
Gdy obrazujemy udziały procentowe jakiś kategorii osobników i zależy nam na podkreśleniu różnic w tych udziałach, to stosujemy wykresy kołowe. Przykładowo gdy porównujemy dwa środowiska, w których wyróżniamy 5 kategorii, a w każdej kategorii znajdujemy pewne liczby obiektów, zobrazowanie tego za pomocą nadrzędnej funkcji graficznej pie() może wyglądać następująco:
srodowisko=c("HALA 1", "HALA 2")
kategoria=c("A", "B", "C", "D", "E")
liczby.w.HALA1=c(234, 456, 211, 98, 14)
liczby.w.HALA2=c(54, 28, 78, 43, 2)
#
windows(5, 2.5)
par(mfcol=c(1,2),mar=c(0.5,0.5,1,0.5))
pie(liczby.w.HALA1, col=rainbow(10)[c(2:4,7,9)], labels=kategoria,
main=srodowisko[1])
pie(liczby.w.HALA2, col=rainbow(10)[c(2:4,7,9)], labels=kategoria,
main=srodowisko[2])
|
Po wykonaniu programu powstanie następujący wykres:
Wykres ten uwidacznia największą różnicę między środowiskami. W środowisku HALA 1 udział procentowy kategorii B i C jest inny niż w środowisku HALA 2.
Graficzne opracowanie skutków katastrofy Tytanika
Wśród na zaimplementowanych do R obiektów jest czterowymiarowa macierz o nazwie Titanic pokazująca liczby osób podróżujących statkiem Tytanik podczas jego pierwszego rejsu zakończonego zderzeniem z górą lodową. Osoby te zostały podzielone na te, które zmarły i te, które przeżyły, na kobiety i mężczyzn, dorosłych i dzieci oraz w zależności od ich statusu majątkowego, czego wskaźnikiem była klasa, którą te osoby podróżowały. Osobną grupę stanowi załoga. Macierz ta wygląda następująco.
> Titanic , , Age = Child, Survived = No # Sex Class Male Female 1st 0 0 2nd 0 0 3rd 35 17 Crew 0 0 # , , Age = Adult, Survived = No # Sex Class Male Female 1st 118 4 2nd 154 13 3rd 387 89 Crew 670 3 # , , Age = Child, Survived = Yes # Sex Class Male Female 1st 5 1 2nd 11 13 3rd 13 14 Crew 0 0 # , , Age = Adult, Survived = Yes # Sex Class Male Female 1st 57 140 2nd 14 80 3rd 75 76 Crew 192 20 |
Aby przekonać się, którymi zmiennymi są poszczególne wymiary tej macierzy, można zastosować funkcję dimnames().
> dimnames(Titanic) $`Class` [1] "1st" "2nd" "3rd" "Crew" # $Sex [1] "Male" "Female" # $Age [1] "Child" "Adult" # $Survived [1] "No" "Yes" |
Z Takiego układu wynika, że Titanic[,,,”No”] to macierz trójwymiarowa pokazująca liczby osób zmarłych podczas katastrofy, a Titanic[,,,”Yes”] pokazuje liczby osob, które przeżyły. Zapis [1,1,1,”No”] pokazuje liczbę osób zmarłych z pierwszej klasy, dzieci płci męskiej, [1,1,2,”No”] to liczba pasażerów zmarłych z pierwszej klasy dorosłych płci męskiej. Mozna to wykorzystać do przedstawienia proporcji zmarłych i przeżywających katastrofę samych pasażerów w zależności od ich płci i statusu majątkowego (wtedy sumujemy dzieci i dorosłych określonej płci) oraz w zależności od wieku pasażerów i statusu majątkowego (wtedy sumujemy dziewczynki i chłopców oraz dorosłych: kobiety i mężczyzn). Przedstawiono to w następującym skrypcie:
nazwy1 = c("1 klasa", "2 klasa", "3 klasa", "Załoga")
nazwy2 = c("mężczyźni","kobiety")
nazwy3 = c("dzieci", "dorośli")
nazwy4 = c("Zmarli", "Przeżyli")
Titanic1=Titanic[,,"Child",]+Titanic[,,"Adult",]
windows(5, 6)
par(mar=c(0,0,1,0), mgp=c(1.7,0.5,0), mfrow=c(3,2))
for (i in 1:3) for (j in 1:2) pie(c(Titanic1[i,j,"No"],Titanic1[i,j,"Yes"]),
col=c("black", "grey"), labels=nazwy4, ps=12,
main=paste(nazwy1[i],nazwy2[j]))
#
Titanic2=Titanic[,"Male",,]+Titanic[,"Female",,]
windows(5, 6)
par(mar=c(0,0,1,0), mgp=c(1.7,0.5,0), mfrow=c(3,2))
for (i in 1:3) for (j in 1:2) pie(c(Titanic2[i,j,"No"],Titanic2[i,j,"Yes"]),
col=c("black", "grey"), labels=nazwy4, ps=12,
main=paste(nazwy1[i],nazwy3[j]))
|
Skrypt ten generuje następujące zestawienia wykresów kołowych:
Pokazują one zasady jakimi kierują się ludzie w sytuacji, gdy trzeba wybierać kogo ocalić, a kogo nie. Historia nie dała nam bardziej przekonującego dowodu, że w sytuacji, gdy trzeba dokonać takiego wyboru, gatunek nasz skłonny jest chronić najmłodszych, kobiety i także najbogatszych.