Wykresy pudełkowe, zastosowanie

Wykres pudełkowy dla mediany

Wykres pudełkowy znacznie lepiej od wykresów słupkowych oddaje ideę rozkładu danych w postaci pewnej wartości centralnej i wielkości charakteryzującej zakres skupiania się danych wokół tej wartości. Stosowany jest tylko dla zmiennych liczbowych i przeważnie dla zmiennych ciągłych. Zmienne dyskretne tak charakteryzowane musi cechować duża zmienność potencjalnych wyników (np. może to być liczebność populacji).

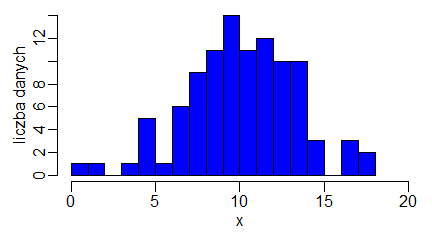
Możemy to zobrazować rysując sobie rozkład z dużej próby za pomocą funkcji hist() oraz rysując dla niego wykres pudełkowy za pomocą funkcji boxplot().

x=c(13.75, 7.20, 7.39, 0.60, 12.55, 9.18, 9.21, 14.51, 11.08, 5.57, 10.88, 13.31,
11.47, 9.79, 4.64, 9.85, 12.63, 9.91, 10.23, 6.44, 2.00, 4.73, 13.63, 9.76,
17.93, 7.08, 14.32, 11.21, 10.10, 12.03, 10.43, 9.41, 7.12, 10.75, 10.79, 
8.73, 11.53, 12.20, 12.36, 13.88, 10.59, 13.49, 9.57, 10.20, 9.44, 12.76, 
11.51, 6.96, 3.90, 13.54, 7.32, 11.16, 12.15, 9.55, 4.50, 4.38, 11.13, 13.07, 
7.49, 16.59, 4.40, 8.69, 7.13, 8.61, 8.74, 13.14, 9.60, 6.98, 8.38, 8.96, 
11.98, 8.30, 11.26, 8.86, 16.08, 11.36, 6.53, 12.34, 8.76, 14.45, 16.08, 8.43, 
11.49, 9.42, 10.66, 12.56, 12.51, 17.82, 8.86, 13.14, 9.74, 7.86, 13.26, 
11.17, 10.93, 7.95, 6.16, 6.22, 10.17, 9.84)

windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
hist(x, xlab="x", ylab="liczba danych",, main="", breaks=20, xlim=c(0,20), 
   col="blue")

windows(4.5, 2.5)
par(mar=c(0.5, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(x, range=0, xlab="", ylab="x", col="blue")

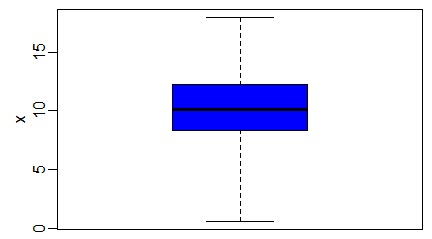
Efektem wykonania tego programu są dwa wykresy:

Wykres pudełkowy pokazał zakres danych od najmniejszej do największej (pionowa przerywana kreska) oraz w jakim zakresie zmieściła się połowa danych (długość pudełka). Upraszcza (choć jednak także trochę zafałszowuje) interpretację uzyskanych wyników, ale jedocześnie umożliwia porównanie obok siebie kilku rozkładów.

Standardowo, gruba kreska w pudełku, oznacza medianę z próby, dolna krawędź pudełka jest pierwszym kwartylem z próby, a górna krawędź pudełka jest trzecim kwartlem z próby.

Mediana definiowana jest dwojako:

• Jako kwantyl rzędu 0.5
• Jako wartość środkowa w próbie uporządkowanej od wartości najmniejszych do największych (w próbie o parzystej liczbie elementów jest średnią dwóch wartości najbliższych środkowi)

Pierwsza definicja dotyczy rozkładu, nadrzędnej charakterystyki populacji statystycznej z której losuje się próby (i uważa się, że rzeczywiste dane także są efektem losowego rozkładu wartości między obiekty biologiczne). Druga definicja to mediana z próby – zgrubne, ale najlepsze z możliwych oszacowanie mediany wg pierwszej definicji.

W podobny sposób definiowane są kwartyle.

• Pierwszy kwartyl to kwantyl rzędu 0.25, trzeci kwartyl to kwantyl rzędu 0.75.
• Pierwszy kwartl z próby to wartość oddzielająca 1/4 najmniejszych wartości od pozostałych, a trzeci kwartyl z próby to wartość oddzielająca 3/4 wartości od pozostałych, w próbie uporządkowanej od wartości najmniejszych do największych.

W obu definicjach pojawiają się kwantyle pewnego rzędu. To termin statystyczny odnoszący się do nieskończonych rozkładów liczbowych. Dla skończonego ciągu a₁,a₂,…a_n kwantyl rzędu p wylicza się jako liczbę q taką, że liczba danych spośród  a₁,a₂,…a_n  mniejszych od q podzielona przez n jest jak najbliższa liczbie p. Na ogół liczb takich jest nieskończenie wiele i obejmują pewien odcinek (a_i,a_j). Kwantyl ustalany jest jako liczba (1-λ)a_i+λa_j dla pewnej liczby λ z przedziału [0,1]. W R wyróżnia się 9 metod wylicznia tego parametru, o czym można przeczytać w opisie funkcji quantile() wyliczającej kwantyl rzedu p dla dowolnego wektora. Wystarczy wpisać do konsoli ?quantile lub help(quantile). Domyślnie zastosowany jest typ siódmy o dość złożonym wzorze i ten kwantyl jest stosowany przez funkcję boxplot() .

Wykres pudełkowy dla średniej

Mediany i kwartyle są popularną charakterystyką danych uzyskanych w badaniach medycznych. W biologii stosuje się ją dla małych prób lub dla bardzo skośnych i nieregularnych rozkładów. Znacznie jednak częściej używa się średnich i odchyleń standardowych z próby. Są one najlepszym oszacowaniem wartości oczekiwanej i odchylenia standardowego – charakterystyk rozkładu, z którego pochodzi nasza próba danych.

Wykres pudełkowy dla średniej i odchylenia standardowego z próby uzyskamy także za pomocą funkcji boxplot() wykorzystując własność, że w pięcioelementowym uporządkowanym wektorze (x₁, x₂, x₃, x₄, x₅) wartością minimalną jest x₁, x₂ jest pierwszym kwartylem z próby, x₃ jest medianą, x₄ jest trzecim kwartylem, a x₅ jest wartością maksymalną. Najczęściej wystarczy zatem zrobić boxplot() dla wektora:

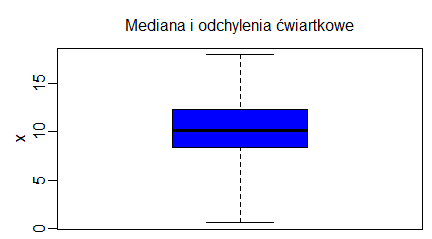
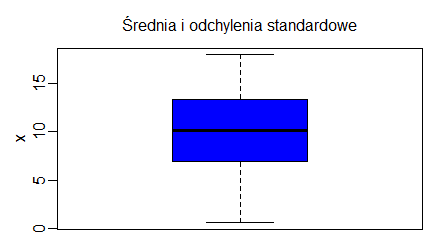
(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x))aby uzyskać wykres pudełkowy ze średnią i odchyleniem standardowym. Porównanie obu boxplotów (dla mediany i dla średniej) pokazuje następujący program:

x=c(13.75,7.20,7.39,0.60,12.55, 9.18, 9.21, 14.51, 11.08, 5.57, 10.88, 13.31, 
11.47, 9.79, 4.64, 9.85, 12.63, 9.91, 10.23, 6.44, 2.00, 4.73, 13.63, 9.76, 
17.93, 7.08, 14.32, 11.21, 10.10, 12.03, 10.43, 9.41, 7.12, 10.75, 10.79, 
8.73, 11.53, 12.20, 12.36, 13.88, 10.59, 13.49, 9.57, 10.20, 9.44, 12.76, 
11.51, 6.96, 3.90, 13.54, 7.32, 11.16, 12.15, 9.55, 4.50, 4.38, 11.13, 13.07,
7.49, 16.59, 4.40, 8.69, 7.13, 8.61, 8.74, 13.14, 9.60, 6.98, 8.38, 8.96, 
11.98, 8.30, 11.26, 8.86, 16.08, 11.36, 6.53, 12.34, 8.76, 14.45, 16.08, 8.43,
11.49, 9.42, 10.66, 12.56, 12.51, 17.82, 8.86, 13.14, 9.74, 7.86, 13.26, 
11.17, 10.93, 7.95, 6.16, 6.22, 10.17, 9.84)
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(x, range=0, xlab="", ylab="x", col="blue")
title("Mediana i odchylenia ćwiartkowe", cex.main=1, font.main=1)
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(c(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x)), range=0, 
      xlab="", ylab="x", col="blue")
title("Średnia i odchylenia standardowe", cex.main=1, font.main=1)

W obszarze od x₁=średnia – odchylenie standardowe do x₂=średnia + odchylenie standardowe, mieści się w przybliżeniu 70% danych. Stąd pudełka dla takich charakterystyk rozkładu są dłuższe.

Pokazana procedura nie sprawdza się, gdy w próbie są dane tak bardzo odbiegających innych wartości, że mean(x)-sd(x) jest mniejsze od min(x) lub mean(x)+sd(x) jest większe od max(x). Wtedy funkcja boxplot() zastosowana na wektorze (min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x) ) nie rysuje tego, co trzeba. Aby wykonać poprawne wykresy należy zmodyfikować wartości kryjące się pod min(x) i max(x)

x=c(1.03, 31.49, 18.49, 22.23, 32.96, 26.48, 31.58, 21.26, 24.64, 234.69)
y=c(219.97, 220.35, 218.44, 251.17, 2.00, 215.33, 215.36)
xs=c(min(x), mean(x)-sd(x), mean(x), mean(x)+sd(x), max(x))
ys=c(min(y), mean(y)-sd(y), mean(y), mean(y)+sd(y), max(y))
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(xs, ys, range=0, xlab="", ylab="x", col="blue")
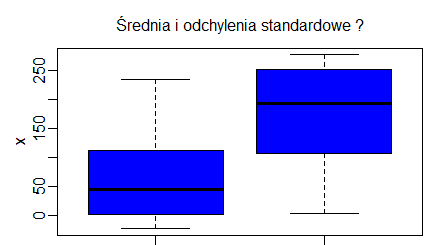
title("Średnia i odchylenia standardowe ?", cex.main=1, font.main=1)
#
if (xs[2]<xs[1]) xs[1]=xs[2]
if (xs[4]>xs[5]) xs[5]=xs[4]
if (ys[2]<ys[1]) ys[1]=ys[2]
if (ys[4]>ys[5]) ys[5]=ys[4]
#
windows(4.5, 2.5)
par(mar=c(0.5, 3, 2.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(xs, ys, range=0, xlab="", ylab="x", col="blue")
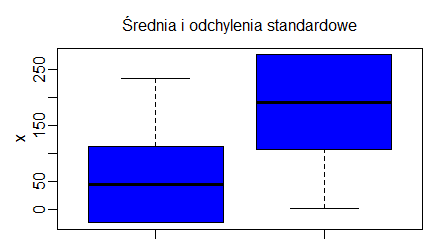
title("Średnia i odchylenia standardowe", cex.main=1, font.main=1)

Program wygenerował dwa wykresy:

Drugi wykres, może niezbyt elegancki ze względu na ogromne odchylenia standardowe i dolną część pierwszego pudełka umieszczającą w obrębie liczb ujemnych, jest poprawny. W praktyce, przy analizie prób z wartościami znacznie odbiegającymi od pozostałych często opisuje się je osobno, a tabele, wykresy i analizy statystyczne wykonuje się dla pozostałych danych.

Test chemotaksji dla Caenorhabditis elegans, zastosowanie mediany

Nicień Caenorhabditis elegans należy do organizmów modelowych, na którym wykonuje się szereg badań fizjologicznych, między innymi bada przesyłanie sygnałów między neuronami. Poprzez stosowanie różnych substancji chemicznych można neurony blokować lub wywoływać błędy w przepływie impulsów nerwowych. Jednym ze sposobów wykazania, że jakaś substancja zmienia przepływ sygnałów między neuronami, jest test chemotaksji.

Test ten polega na umieszczenie w jednym końcu szalki petriego substancji wabiącej nicienie, w drugim końcu wypuszcza się nicienie w ilości około 100 osobników. Eksperyment wykonuje się jednocześnie na dwóch szalkach dla grupy testowej nicieni potraktowanych uprzednio substancją chemiczną i dla grupy kontrolnej. Po 60 minutach sprawdza się ile nicieni dotarło do obszaru, gdzie wylano substancję wabiącą.

Liczby nicieni

Grupa kontrolna

Grupa testowa

w obszarze substancji wabiącej

wszystkich wypuszczonych

Następnie wylicza się indeks chemotaksji w postaci M_c/N_c-M_t/N_t bądź (M_c/N_c-M_t/N_t)*100%. Gdy jakaś substancja istotnie blokuje neurony nicienia, indeks ten jest dodatni i bliski jedynce.

Najczęściej tego typu eksperyment powtarza się wielokrotnie i porównuje ze sobą wyniki uzyskane dla różnych dawek substancji czynnej, w różnych temperaturach itp. Przykładem takich badań było stosowanie czterech dawek anestetyku – azydku sodu NAN3, którymi potraktowano najpierw nicienie, a następnie wykonano na nich test chemotaksji. Dla każdej dawki oraz dla kontroli test ten powtórzono 6-krotnie. Uzyskano następujące wyniki (liczby nicieni, które po godzinie dotarły do substancji wabiącej oraz liczby wszystkich nicieni na szalce), co zapisano w postaci K/N:

1

98/101

93/102

87/102

26/98

5/103

2

95/98

88/104

78/101

32/93

11/107

3

76/96

75/99

47/99

15/98

4/96

4

45/96

30/98

12/93

3/101

1/100

5

83/97

85/103

55/92

9/94

0/96

6

94/94

97/99

86/103

33/104

16/107

Dane takie powinny być najpierw zaimportowane do R w postaci bazy danych o kolumnach: Powtórzenie, Dawka, Liczba wypuszczonych nicieni (N), liczba nicieni w obszarze substancji wabiącej (K). Nazwom tym nadano stosowne skróty i utworzono następującą ramkę danych:

K0=c(98,95,76,45,83,94)
N0=c(101,98,96,96,97,94)
K0.1=c(93,88,75,30,85,97)
N0.1=c(102,104,99,98,103,99)
K0.5=c(87,78,47,12,55,86)
N0.5=c(102,101,99,93,92,103)
K1=c(26,32,15,3,9,33)
N1=c(98,93,98,101,94,104)
K5=c(5,11,4,1,0,16)
N5=c(103,107,96,100,96,107)
baza=data.frame(POWT=rep(1:6,5), 
  DAWKA=c(rep(0,6),rep(0.1,6),rep(0.5,6),rep(1,6),rep(5,6)),
N=c(N0,N0.1,N0.5, N1, N5), K=c(K0, K0.1, K0.5, K1, K5))

W teorii statystycznej nikt nie poleca wyliczanie średniej z procentów. Wynika to stąd ze procent wyliczony na dużej próbie jest bardziej wiarygodny od procentu wyliczonego na małej próbie. Gdybyśmy chcieli narysować procent nicieni, które dotarły do substancji wabiącej, musielibyśmy dla każdej dawki zsumować liczby nicieni ze wszystkich powtórzeń (zarówno wszystkich jak i tych, które dotarły do celu) i wyliczyć stosowny procent. Taki procent zazwyczaj pokazuje się w postaci słupków. Jego wykonanie wyglądałoby następująco:

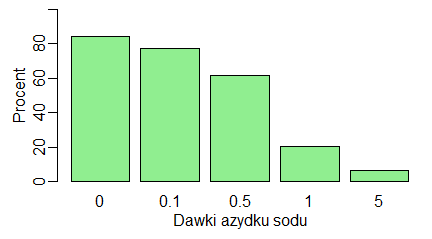
agN=aggregate(N~DAWKA, baza, sum)
agK=aggregate(K~DAWKA, baza, sum)
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
barplot(agK[,2]/agN[,2]*100, names.arg=agN[,1],
ylim=c(0,100),
xlab="Dawki azydku sodu", ylab="Procent", col="lightgreen")

Program ten utworzy następujący wykres:

W przypadku testu chemotaksji wypuszcza się na szalki duże i zbliżone do siebie liczby nicieni (ich dokładną liczbę określa się dopiero po zakończeniu eksperymentu) i znacznie ważniejsze od zróżnicowania liczby wypuszczonych nicieni, wydają się zmiany warunków wykonywania powtórzeń eksperymentu (często robi się to w kolejnych dniach, albo rzadziej, przy nieco innej temperaturze, oświetleniu itp.) i zmiany jakie w tym czasie zaszły w populacji, na której wykonuje się eksperyment. Standardowo wylicza się współczynnik chemotaksji dla każdego powtórzenia osobno, a uzyskane wyniki charakteryzuje się medianą i odchyleniami ćwiartkowymi. Ostatnio standardem stało się zaznaczanie na wykresach danych (zazwyczaj jest mniej niż 20) w postaci punktów, przy czym, aby nie pokrywały się one ze sobą, daje się im losową pierwszą współrzędną, nie mniej bliską środkowi pudełka, na którym są zaznaczane. Przygotowanie danych i wykonanie wykresu wygląda następująco:

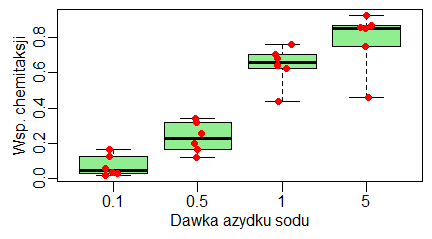
P0=baza[baza$DAWKA==0,4]/baza[baza$DAWKA==0,3]
ChemTax0.1=P0 - baza[baza$DAWKA==0.1,4]/baza[baza$DAWKA==0.1,3]
ChemTax0.5=P0 - baza[baza$DAWKA==0.5,4]/baza[baza$DAWKA==0.5,3]
ChemTax1=P0 - baza[baza$DAWKA==1,4]/baza[baza$DAWKA==1,3]
ChemTax5=P0 - baza[baza$DAWKA==5,4]/baza[baza$DAWKA==5,3]
#
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(ChemTax0.1, ChemTax0.5, ChemTax1, ChemTax5,
range=0, names=paste(c(0.1, 0.5, 1, 5)),
xlab="Dawka azydku sodu", ylab="Wsp. chemitaksji", col="lightgreen")
points(rnorm(6,1,0.05), ChemTax0.1, pch=19, col="red")
points(rnorm(6,2,0.05), ChemTax0.5, pch=19, col="red")
points(rnorm(6,3,0.05), ChemTax1, pch=19, col="red")
points(rnorm(6,4,0.05), ChemTax5, pch=19, col="red")

Wykres utworzony przez ten program wygląda następująco:

Ze względu na element losowy stosowany przy ustalaniu współrzędnej poziomej czerwonych punktów, powtórzenie kodu rysowania wykresu spowoduje powstanie nieco innego ułożenia czerwonych kropek. Należy wybrać taki wykres, w którym można doliczyć się na pasie każdego pudełka 6 różnych punktów. Tego typu wykresy są standardem przy pokazywaniu indeksu chemotaksji uzyskanego eksperymentalnie.

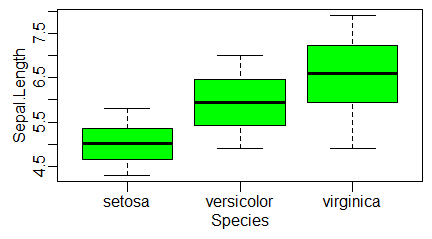
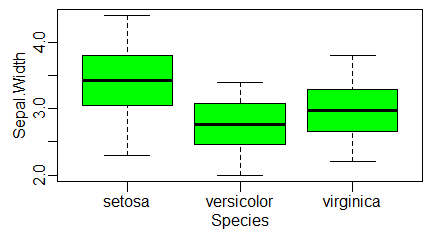
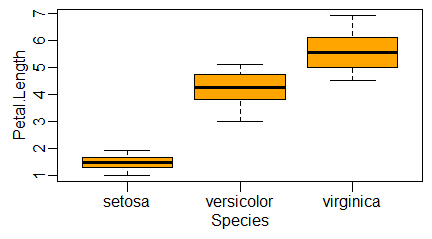
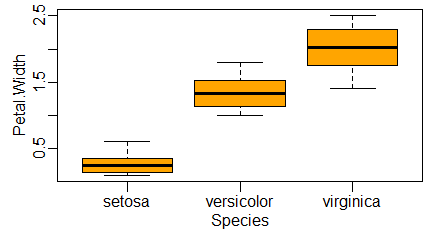
Długość i szerokość płatków okwiatu i działek kielicha trzech gatunków irysów, obrazowanie średnich

W zaimplementowanej do R bazie iris pokazano wyniki pomiarów długości i szerokości płatków okwiatu i płatków kielicha trzech gatunków irysów. Typowym sposobem zobrazowania tych wyników są pudełka ze średnimi i odchyleniami standardowymi wyników pomiarów. Tych zmiennych ciągłych jest cztery. Ich nazwy i numer kolumny, w której są umiejscowione, najlepiej jest uzyskać stosując funkcję str(iris).

> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

Aby zastosować funkcję graficzną boxplot() do uzyskania stosownych wykresów należy wyliczyć dla każdej zmiennej ciągłej, dla każdego gatunku irysa wielkości: wartość minimalną (funkcja min()), średnią minus odchylenie standardowe (mean()-sd()), średnią (mean()), średnia plus odchylenie standardowe (mean()+sd()), oraz wartość maksymalną (funkcja max()). Wyliczanie tych wielkości można skrócić stosując pętle i funkcję aggregate(). Pętlę można zastosować robiąc obliczenia dla wszystkich kolumn dla których rysujemy wykres pudełkowy. W bazie iris wykorzystano fakt, że zmienne ciągłe zajmują cztery pierwsze kolumny bazy danych. Gdy zdarzy się, że zmienne, dla których zastosować pętle, zajmują kolumny 2, 4, 6 i 7, możemy także stosować pętlę w postaci for (i in c(2,4,6:7)) {}. Funkcję aggregate() natomiast stosujemy, by uzyskać odpowiednie wartości od razu dla trzech gatunków irysów.

Uzyskanie odpowiednich wartości do zrobienia czterech wykresów pudełkowych z trzema pudełkami na każdym, może wyglądać następująco:

#Wyliczanie min(), mean()-sd(), mean(), mean()+sd() i max() 
#dla 4 różnych zmiennych ciagłych.
MIN=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, min)[,2]->x
MIN=cbind(MIN,x)}
names(MIN)[2:5]=names(iris)[1:4]

MEAN.minus.SD=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, 
     function(x) mean(x)-sd(x))[,2]->x
MEAN.minus.SD=cbind(MEAN.minus.SD,x)}
names(MEAN.minus.SD)[2:5]=names(iris)[1:4]

MEAN=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, mean)[,2]->x
MEAN=cbind(MEAN,x)}
names(MEAN)[2:5]=names(iris)[1:4]

MEAN.plus.SD=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, 
      function(x) mean(x)+sd(x))[,2]->x
MEAN.plus.SD=cbind(MEAN.plus.SD,x)}
names(MEAN.plus.SD)[2:5]=names(iris)[1:4]

MAX=data.frame(Species=c("setosa", "versicolor","virginica"))
for (i in 1:4) {aggregate(iris[,i] ~ Species, iris, max)[,2]->x
MAX=cbind(MAX,x)}
n#ames(MAX)[2:5]=names(iris)[1:4]

#Poprawki na przypadek, 
#gdy mean-sd<min lub mean+sd>max
for (i in 1:3) for (j in 2:5) if (MIN[i,j]>MEAN.minus.SD[i,j]){
                           MIN[i,j]=MEAN.minus.SD[i,j]}
for (i in 1:3) for (j in 2:5) if (MAX[i,j]<MEAN.plus.SD[i,j]){
                           MAX[i,j]=MEAN.plus.SD[i,j]}

#Połaczenie wyników w jedną bazę
iris_1=rbind(MIN,MEAN.minus.SD,MEAN,MEAN.plus.SD,MAX)

Narysowanie od razu czterech wykresów także można wykonać w pętli:

#Rysowanie 4 wykresów
kolory=c("green","green","orange","orange")
for (i in 2:5) {
windows(4.5, 2.5)
par(mar=c(3, 3, 0.5, 0.5), mgp=c(1.5,0.5,0))
boxplot(iris_1[,i]~Species, iris_1, xlab="Species", ylab=names(iris_1)[i],
col=kolory[i-1])}

Program tworzy cztery następujące wykresy:

Jak można się domyślić, zielone pudełka dotyczą wymiarów działek kielicha, a pomarańczowe – płatków okwiatu.

Stężenie fluoru w wydzielinie gruczołów odbytowych skunksów, mediany i średnie

Pokazanie na jednym wykresie zarówno median jak i średnich tych samych danych jest informacją o skośności rozkładu (gdy mediany znacznie różnią się od średnich) lub o jej braku (gdy obie te charakterystyki prawie się pokrywają). Wielkościom tym powinny towarzyszyć odchylenia ćwiartkowe i standardowe, gdyż tylko wtedy można ocenić wielkość różnicy między medianą a średnią. To dodatkowo pokazuje w jakim zakresie mieści się połowa danych najbliższych medianie i 70% danych najbliższych średniej. Jest to masa dodatkowych informacji charakteryzujących rozkłady danych i warto takie wykresy wykonać. Pozwala to sprawdzić, czy wnoszą one coś nowego do interpretacji danych, czy raczej ją utrudniają.

Obrazowanie zarówno średnich z odchyleniami standardowymi jak i median z odchyleniami ćwiartkowymi na jednym wykresie polega na narysowaniu jednej charakterystyki w postaci pudełka a drugiej w innej formie (najczęściej punktu z odchyleniami w postaci strzałek) nałożonej na to pudełko.

Wykonanie tego typu wykresów pokazano na przykładzie bazy danych dotyczących badań stężenia fluoru w wydzielinie gruczołów odbytowych skunksów, która pokazywana jest na ćwiczeniach z informatyki studentów biologii UW. Baza ta została zaprezentowana w pierwszej części tego podręcznika “R dla biologów, podstawowe operacje” w rozdziale o ramkach danych w podrozdziale “Operacje wykonywane na ramkach danych”.

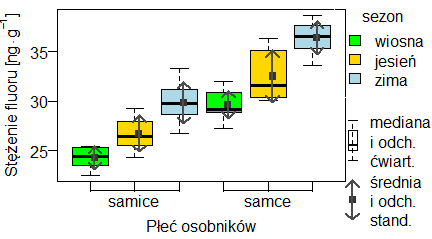
Zobrazowanie median z odchyleniami ćwiartkowymi w postaci pudełka i średnich z odchyleniami standardowymi w postaci punktów ze strzałkami na jednym wykresie wygląda następująco:

skunks$SEZON=ordered(skunks$SEZON, levels=c("wiosna", "jesień", "zima"))
#
windows(4.5, 2.5)
#
par( mar=c(3,3,0.5,4.5), mgp=c(1.8,0.5,0), las=1, xpd=TRUE, ps=12)
#
boxplot(FLUOR ~ SEZON+PLEC, skunks,
col=c("green", "gold", "lightblue"),
names=c(" ", "samice"," ", " ", "samce", " "),
xlab="Płeć osobników",
ylab=expression("Stężenie fluoru [ "* ng %.% g^-1 *"]"))
#
lines(c(1,3),c(21,21))
lines(c(4,6),c(21,21))
#
legend(6.5, 40,
title="sezon",
legend=c("wiosna", "jesień", "zima"),
fill=c("green", "gold", "lightblue"),
box.col="white")
#
sr = aggregate(FLUOR ~ SEZON+PLEC, skunks, mean)
odsd = aggregate(FLUOR ~ SEZON+PLEC, skunks, sd)
xi = 1:6+0.1
points(xi, sr$FLUOR, col = grey(0.2), pch = 15)
arrows(xi, sr$FLUOR - odsd$FLUOR, xi, sr$FLUOR + odsd$FLUOR, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
#
x1=6.8
x2=7
y1=25
y2=27
rect(x1,y1,x2,y2)
lines(c((x1+x2)/2,(x1+x2)/2),c(y1-1,y2+1), lty=2)
lines(c(x1,x2),c(y1+0.5,y1+0.5),lwd=2)
lines(c(x1,x2),c(y1-1,y1-1))
lines(c(x1,x2),c(y2+1,y2+1))
text(x2+0.3,(y1+y2)/2,"mediana\ni odch.\nćwiart.", adj=0)
#
x1=(x1+x2)/2
y1=20
points(x1, y1, col = grey(0.2), pch = 15)
arrows(x1, y1-2, x1, y1 + 2, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
text(x1+0.4,y1,"średnia\ni odch.\nstand.", adj=0)

Po wykonaniu tego programu w R uzyskujemy następujący wykres:

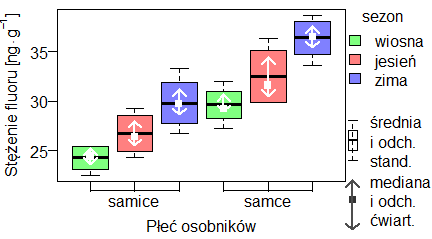
Zobrazowanie średnich z odchyleniami standardowymi w postaci pudełka i median z odchyleniami ćwiartkowymi w postaci punktów ze strzałkami na jednym wykresie wygląda następująco:

skunks$SEZON=ordered(skunks$SEZON, levels=c("wiosna", "jesień", "zima"))
#
# zrobienie wykresów pudełkowych ze średnią i odch. standardowymi.
Min=aggregate(FLUOR ~ SEZON+PLEC, skunks, min)
Sr.minus.sd = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) mean(x)-sd(x))
Sr = aggregate(FLUOR ~ SEZON+PLEC, skunks, mean)
Sr.plus.sd = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) mean(x)+sd(x))
Max = aggregate(FLUOR ~ SEZON+PLEC, skunks, max)
#
# Poprawki na ewentualność Sr.minus.sd<min i Sr.plus.sd>max
for (i in 1:6) if (Min[i,3]>Sr.minus.sd[i,3]) Min[i,3]=Sr.minus.sd[i,3]
for (i in 1:6) if (Max[i,3]<Sr.plus.sd[i,3]) Max[i,3]=Sr.plus.sd[i,3]
#
# Połączenie podbaz
skunks_1=rbind(Min, Sr.minus.sd, Sr, Sr.plus.sd, Max)
#
windows(4.5, 2.5)
par( mar=c(3,3,0.5,4.5), mgp=c(1.8,0.5,0), las=1, xpd=TRUE, ps=12)
#
boxplot(FLUOR ~ SEZON+PLEC, skunks_1,
col=c("#80FF80FF", "#FF8080FF", "#8080FFFF"),
names=c(" ", "samice"," ", " ", "samce", " "),
xlab="Płeć osobników",
ylab=expression("Stężenie fluoru [ "* ng %.% g^-1 *"]"))
#
lines(c(1,3),c(21,21))
lines(c(4,6),c(21,21))
#
legend(6.5, 40,
title="sezon",
legend=c("wiosna", "jesień", "zima"),
fill=c("#80FF80FF", "#FF8080FF", "#8080FFFF"),
bty="n")
#
# Naniesienie median z odchyleniami ćwiartkowymi.
#
Med = aggregate(FLUOR ~ SEZON+PLEC, skunks, median)
Cw0.25 = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) quantile(x,0.25))
Cw0.75 = aggregate(FLUOR ~ SEZON+PLEC, skunks, function(x) quantile(x,0.75))
xi = 1:6
points(xi, Med$FLUOR, col = "white", pch = 15)
arrows(xi, Cw0.25$FLUOR, xi, Cw0.75$FLUOR, code = 3,
col = "white", lwd=2, angle = 45, length = 0.1)
#
x1=6.8
x2=7
y1=25
y2=27
rect(x1,y1,x2,y2)
lines(c((x1+x2)/2,(x1+x2)/2),c(y1-1,y2+1), lty=2)
lines(c(x1,x2),c((y1+y2)/2,(y1+y2)/2),lwd=2)
lines(c(x1,x2),c(y1-1,y1-1))
lines(c(x1,x2),c(y2+1,y2+1))
text(x2+0.3,(y1+y2)/2,"średnia\ni odch.\nstand.", adj=0)
#
x1=(x1+x2)/2
y1=20
points(x1, y1, col = grey(0.2), pch = 15)
arrows(x1, y1-3, x1, y1 + 2, code = 3,
col = grey(0.3), lwd=2, angle = 45, length = 0.1)
text(x1+0.4,y1,"mediana\ni odch.\nćwiart.", adj=0)

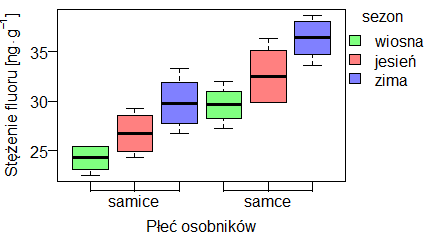
Po wykonaniu pierwszej części tego programu uzyskamy pierwszy wykres, a wykonanie całości – drugi wykres:

Wykres pierwszy jest standardem obrazowania zależności zmiennej ciągłej od zmiennej dyskretnej.